最大团问题的竞争决策算法

黄 飞，宁爱兵，刘志民，何永梅，张惠珍

（上海理工大学 管理学院，上海 200093）

最大团问题（MCP）[1-3]是组合优化中的NP 难题（non-deterministic polynomial problems），在实践中有着广泛的应用，如社会网络分析[4]、生物信息学[5]、分子生物学、编码理论[6]及经济学[7]等，是图论、运筹学及离散数学等领域中一个重要的研究目标。

本文介绍、提出并论证了最大团的部分数学性质，在此基础上设计了一个求解该问题的竞争决策算法（CDA）。为了阐述算法的基本原理，本文给出了一个简单的案例，运用该算法进行手动求解。最后运用该算法对最大团问题的标准测试图进行求解，计算实验得到了较好的结果。测试中有些情况下还可以得到目前最优解，如后面的实例p_hat300-2，MANN_a27 和MANN_a45。

1 竞争决策算法

自从CDA 在文献[8]中提出之后，该算法被应用在了很多NP 问题的求解上，具体可参阅文献[9-13]，且都得到了较好的结果。本文仅给出算法的原理与概念，算法的详细情况可参阅文献[9]。

1.1 原理

竞争决策现象普遍存在于大自然中，这些竞争决策都在一定的法则下进行，且同时受到一种或多种因素的共同影响。竞争决策就是参与竞争的各方根据竞争决策机制分别占据一定的资源的过程。竞争决策之后，会达到一个新的均衡状态。如果新形成的均衡状态优于初始状态，则能实现优化的目的。CDA 就是模拟这个机制来实现优化。它首先根据求解的问题构造出一个或多个竞争参与者，参与对资源的竞争，然后利用相应的竞争机制，通过决策判定竞争者是否占有资源以及占有哪些资源，直至达到均衡状态。

1.2 基本概念

a.竞争者：参与竞争资源的各方，在本文中，如果算法中只存在一个竞争者，则假设存在另一个虚构的竞争者N（可以假定代表自然），同时参与争夺资源。N 没有竞争力函数。

b.资源：竞争者所争夺的目标，整个算法的核心。

c.竞争决策状态：某一瞬间，所有参与竞争的各方各自所占有的资源的一种状态。初始状态下，参与竞争的各方均不占有资源，虚拟竞争者除外，且占有所有资源。

d. 竞争力函数：代表竞争者争夺资源的能力。

e. 决策函数：决策函数起到判定的作用，用于判定资源的分配，分3 种情况。

（a）若除了虚拟竞争者之外只有一个竞争者，决策函数用于判定该竞争者能否从虚拟竞争者那里争夺资源；

（b）若除了虚拟竞争者之外有多个竞争者，决策函数不仅要判定哪些竞争者可以优先占有资源，还要判定这些竞争者具体可以占有哪些资源；

（c）决定是否要从某个竞争者手中强制性地剥夺出资源，并将资源分配给另外一个竞争者。

f. 竞争决策均衡状态：完成资源的初步分配后所达到的一种状态。均衡状态下，非虚拟竞争者不能根据竞争决策机制争夺更多资源，即除非引入资源交换规则，否则将不再进行竞争决策。

g. 资源交换规则：达到均衡状态后，资源交换规则将强制全部或部分竞争者（包括虚拟竞争者）之间相互交换资源，使竞争进入非稳定的均衡状态。非稳定的均衡状态下，非虚拟的竞争者能根据竞争决策机制再次争夺资源，直至达到一个新的均衡状态。进行资源交换后，必须使竞争进入非稳定的状态，这样才能使竞争者对资源再次进行竞争，达到新的竞争决策均衡状态，实现优化的目的。

2 最大团问题的竞争决策算法

2.1 问题介绍

最大团问题描述如下：给定1 个简单无向图G=（V，E），S 是结点集合V 的1 个子集，若S 中任意2 个结点之间都相邻，即由S 导出的子图G[S]是完全子图，且G[S]不包含在图G 的更大的完全子图中，则称G[S]为团。最大团问题就是求出图中结点个数最多的团。

2.2 数学符号

G=（V，E）：G 代表简单的无向图，V 代表图的结点集合，E 代表图的边集，且E 由V 中的结点对表示。

n：图中结点的个数。

N（v）：结点v 的开邻集，所有与结点v 相邻的点的集合。

N[v]：结点v 的闭邻集，即N（v）∪{v}。

d（v）：结点v 的度，即集合N（v） 中所包含的结点的个数。

G[V1]：G[V1]是图G=（V，E）的点导出子图，G[V1]=（V1，E1），其中，V1⊂ V ，E1⊂ E，且对于图G 中的每一条2 个端点都在V1中的边ei都有ei∈E1。

G1：初始状态下，G1等于原图G，即G1=（V，E）=（V1，E1）。

d（vi）：结点vi的度，即图G 中与vi相邻的点的个数。

d1（vi）：结点vi的度，即图G1中与vi相邻的点的个数。

p（i）：结点vi在G1图中的竞争力函数。

Gb：算法在均衡时所求得的最大完全子图。

Vad：与完全子图Gb中各个结点相邻结点的集合，即

Gmax：目前为止算法中所发现的最大团。

|G|：G 图中所包含的结点的个数。

|V|：结点集合所包含的结点个数。

2.3 数学性质

现仅给出竞争决策算法所涉及到的最大团的数学性质，性质1～3 的证明参阅文献[9−10]。推论1 及性质4 为本文提出的。算法中，推论1 用于删除冗余结点，性质4 用于资源交换。

性质1若结点集合V 中某个结点v 的度是0，那么，v 必然不属于所求的最大团的结点集合S[14]。

性质2若结点集合V 中某结点v 的度为n−1，那么，v 必然属于所求的最大团的结点集合S。

性质3S 为求得的最大团的结点集合，若v∈S 且d（v）=k；那么， | S|k+1[15]。

推论1设已求出的最大完全子图为Gmax，其结点个数为|Gmax|，G1中某一结点v 的度d（v）=k，如果k<|Gmax|，则可以将v 从G1中删除，从而使问题得到简化。

证明根据性质3 可得，度为k 的结点v 所在的完全子图最多有k+1 个顶点，若k |Gmax|−1，则包含v 的完全子图的顶点个数最多为|Gmax|个，不大于已求出的最大完全子图Gmax的结点个数，所以，将v 作为冗余结点从G1中删除，从而使问题得到简化而不影响求解结果。

性质4G2=（V2，E2）是G1=（V1，E1）的1 个子图，且是完全图，若V3⊂ V1−V2，G3=（V3，E3）=G[V3]，V4⊂ V2，V3与V2−V4中的所有结点都相邻，若|V3|>|V4|，那么，将V4从G2中删除，将V3加入G2，此时，G2为更大的完全子图。

证明G3本身是1 个完全子图，且V3中的所有结点与V2−V4中的所有结点都相邻，因而新生成的图G2是1 个结点个数更多的完全子图。

2.4 算法思想

在CDA 中，结点是竞争者争夺的资源，所需求解的最大团是竞争者A，同时参与竞争的是虚拟竞争者N。初始状态时，虚拟竞争者N 占有全部结点，竞争者A 不占有任何结点。达到均衡状态时，竞争者A 具有的结点即为所求的最大团。

2.5 初始状态、竞争力函数、决策函数、资源交换规则

a.初始状态。

对于含有n 个结点的图，一共有n 个初始状态，将结点按各个度的大小降序排列之后，第i 个初始状态为竞争者A 仅占有资源vi，其余结点资源都被虚拟竞争者N 所占有。在每个初始状态开始时需要检查d（vi）是否小于已知最大完全子图中结点的个数，若是，则该初始状态不会出现更好的解且放弃掉该初始状态。

b.竞争力函数。

采用一个竞争力函数

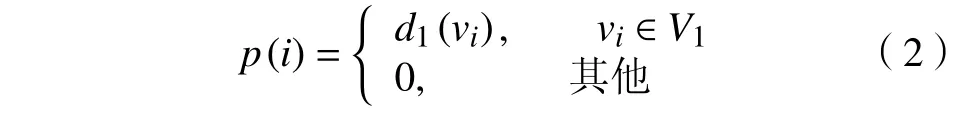
c.决策函数。

本文只有一个决策函数，即在竞争中将竞争力函数值p（i）最大的结点优先加入到图Gb中，当多个结点的竞争力函数值相等时，则将编号小的结点加入到图中。

d.资源交换规则。

资源交换规则见下面的算法流程。

2.6 算法的过程

算法的过程如下：

a.初始图Gb和Gmax是1 个没有结点、没有边的空图，首先将G1中竞争力函数p（i）最大的点vi加入Gb中，然后将Vad中竞争力函数值p（i）最大的结点加入到Gb中。根据式（1）重新计算Vad，持续该步骤，直到Vad为空集。

b.检查是否存在冗余结点，如果存在冗余结点，则删除冗余结点并更新竞争力函数。具体的做法参见下面的算法流程。

c.执行资源交换，交换后再次检查是否存在冗余结点，如果存在，则剔除冗余结点后更新竞争力函数。详细的内容见下面的算法流程。

2.7 算法流程

步骤0k=1；将结点按各个结点的度从大到小排序，Vmax={ }，Emax={ }，Gmax=（Vmax，Emax）。

步骤1初始化。

设置初始状态。竞争者A 只占有资源vk，其余结点都被虚拟竞争者N 占有。由推论1 可知，若|d（vi）|<|Vmax|，则该初始状态不会出现更好的解，因此，此时跳到步骤3 而放弃该初始状态；否则，继续执行下面的操作：

G1=（V1，E1）=（V，E）=G，从G1中删除结点vk以及不与vk相邻的所有结点，Vb={vk}，Eb={ }，Gb= （Vb，Eb），Vi={vk}，V*={ }，E*={ }，G*=（V*，

步骤2竞争决策。

根据式（2），计算初始状态下竞争者A 对结点资源的竞争力函数值p（i），并降序排列。

a.本轮竞争阶段1：资源分配阶段。

（a）根据性质1，删除竞争力函数值为0 的结点，若删除后G1为空集，算法结束，问题没有意义。

根据性质2 将度为n−1 的结点全部放入Gb中。

（b）根据式（1）计算Vad，并将Vad中竞争力函数值p（i）最大的结点加入到Gb中，之后重新计算Vad，持续该过程，直到Vad为空集。此时得到的图是1 个完全子图，且结点个数为|Gb|。若|Gb|>|Gmax|，则|Gmax|=|Gb|；否则，执行步骤c。

b.本轮竞争阶段2：删除冗余结点。

利用推论1 删除冗余结点，即将图G1中度小于|Gmax|的顶点删除，并重新计算G1中结点的竞争力函数，降序排列，输出图G1此时的结点个数n。

c.本轮竞争阶段3：资源交换阶段。

为了提高算法的速度，本算法只找出性质4 中|V3|=2 且|V4|=1 的结点，用V3中的2 个结点交换V4中的1 个结点，这样能得到一个更大的完全子图Gb。持续查找和替换这种操作，直至图G1中不存在这种满足资源交换条件的结点。此时，若|Gb|>|Gmax|，则|Gmax|=|Gb|，利用推论1 删除冗余结点；否则，舍弃Gb，执行步骤3。

步骤3k=k+1，若k n，则跳到步骤1；否则，跳到步骤4。

步骤4算法结束。

输出竞争决策的结果。

3 算法的时间复杂度分析

步骤2的a 最坏的情况下时间复杂度为O（n2）；步骤2 的b 剔除图中冗余结点在最坏的情况下时间复杂度为O（n）；步骤2 的c 最多执行的次数为n 次，1 个初始状态查找并执行1 次交换的时间复杂度为O（n2），因此，步骤2 的c 在最坏的情况下时间复杂度为O（n3）。综上所述，该算法的时间复杂度为O（n3）。

4 示例分析

现给出1 个案例来阐述算法的原理以及过程，同时也只给出第1 个初始状态下的竞争决策过程，如图1 所示。

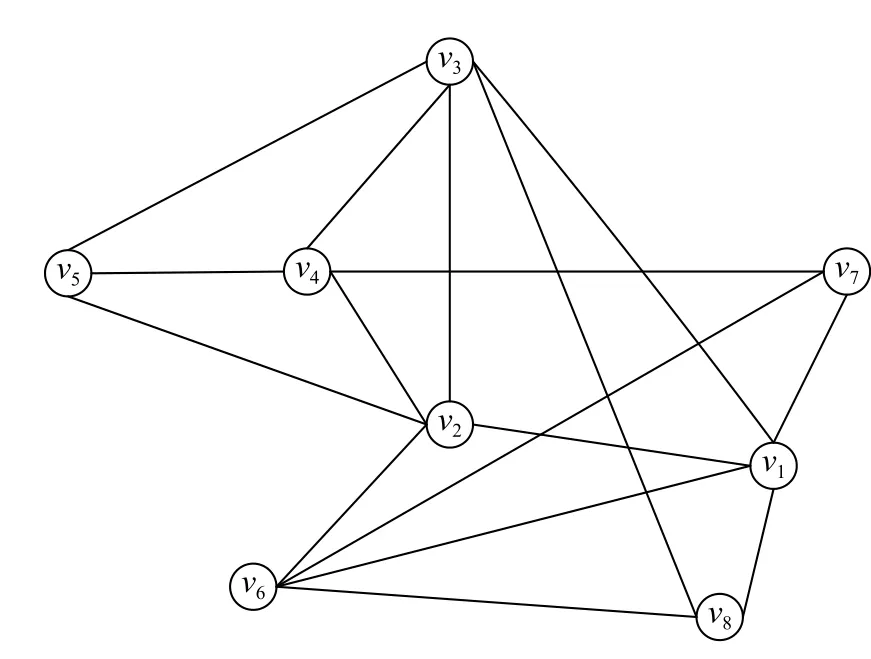
图1 示例图G1Fig.1 Sample graph G1

竞争决策计算如下：

a.初始化阶段。

给出第1 个初始状态下的竞争决策过程，因此，最开始时可以设置竞争者A 没有占有资源结点v1，其他结点资源都被虚拟竞争者N 占有。从图G1中删除v1以及不与v1相邻的所有结点v4和v5，V=V1={v2，v3，v6，v7，v8}，G1=（V，E）=（ V1， E1） ， Gb=（ Vb， Eb） ， Vb={v1}， Eb={ }，Gmax=（Vmax，Emax），Vmax={v1}，Emax={ }。

b.资源分配阶段。

根据式（1）可得集合Vad={v2，v3，v6，v7，v8}，计算竞争力函数，p（1）=0，p（2）=5，p（3）=5，p（4）=0，p（5）=0，p（6）=4，p（7）=3，p（8）=3。

将Vad中竞争力函数值最大的1 个结点加入Vb中，如果存在若干个竞争力函数值最大的结点，任选1 个加入到Vb中。因此，先将v2加入到Vb，再重复计算1 次后将v3也加入到Vb，此时得到1 个团Vb={v1，v3，v2}，且Vad为空集。

因 初 始 时Vmax={v1}， 所 以， 此 时 满 足|Gb|>|Gmax|，将Gb中的结点放入Gmax，|Gmax|=3，Vmax={v1，v3，v2}。

c.根据b 删除图中冗余结点。

删除V1中度小于 |Vmax|=3 的所有结点及与其相连的边，因图中所有结点的度都大于等于3，所以，此过程没有冗余结点被删除。

d.资源交换阶段。

找出性质4 中|V3|=2 且|V4|=1 的结点，此时找到V3={v4，v5}，V4={v1}，用V3中的2 个结点替换V4中的1 个结点，从而得到1 个更大的完全子图Gb=（Vb，Eb），其 中，Vb=Vmax={v2，v3，v4，v5}，该完全子图如图2 所示。在图1 中利用推论1 删除冗余结点，即将图1 中度小于|Vmax|=4 的顶点 删除，据此 依次 删 除v7，v8，v6，v1，v2，v3，v4，v5，图1 变 为 空 图，因 此，S={v2，v3，v4，v5}为最优解。虽然这个实例得到了最优解，但是，这个算法并不能保证求解所有的实例时都能得到最优解。

e.输出竞争决策结果。

Vmax={v2，v3，v4，v5}，最优，其代表的图如图2 所示。

图2 最大团的图Fig.2 Graph of maximum clique

5 数值计算及分析

为了对算法的有效性进行验证，用Java 语言在PC 机上进行计算实验。运用本算法对DIMACS(The Center for Discrete Mathematics and Theoretical Computer Scinence)的基准图进行求解，并与目前最好的结果进行比较，如表1 所示，相关的测试实例可以登录http://iridia.ulb.ac.be/~fmascia/maximum_clique/DIMACS-benchmark#detDSJC1000_5 下载。

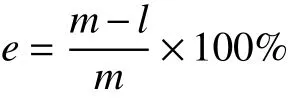
式中：e 为误差率；m 为目前最好解；l 为本文解。

最大团问题是NP 难解问题，除非能够证明所有NP 问题都可以转化为具有多项式算法的判定问题，否则不存在多项式时间的精确算法。精确算法能够求出最优解，但是，求解时间随着问题规模的增大而呈指数增长，时间复杂度较高。启发式算法求解速度快，但是，一般情况下不能找到最优解，只能找到近似解或者局部最优解。本文的竞争决策算法是启发式算法，利用本文算法对基准图进行计算求解，在Eclipse 软件上运行，从表1 中可以看出，利用CDA 求得的解，和最优解之间的误差率基本保持在10%以内。有些示例可以取得与目前最好的结果相同的解，如示例hamming8−4 和示例p_hat300−2，有些示例可以取得与目前最好结果极其相近的解，如示例C125.9，MANN_a27，MANN_a45。作 为 比 较，Belachew 等[11]用秩为1 的对称非负矩阵逼近算法求解DIMACS 中的示例， 求解示例C500.9，MANN_a27，p_hat1500−2，p_hat1500−3 得到的最好解分别为50，123，61，92，而本文的求解结果分别为52，125，59，85。文献[16]还将求解结果与其他2 个启发式算法的求解结果进行比较，结果显示，启发式算法在求解的36 个案例中，只有 3个案例得到了与该算法相近的解。

表1 CDA 算法结果与目前最好结果的比较Tab.1 Comparison between the results of CAD algorithum and the best results at present

6 结束语

竞争决策算法是解决组合优化问题的有效算法，该算法根据所求解的问题的数学性质设计出竞争规则、竞争力函数、决策函数以及设定初始格局就能很好地求解组合优化问题。求解最大团问题时，该算法在资源分配阶段即可形成1 个初始解，根据性质4 判断是否存在满足资源交换条件的结点，若存在则进入资源交换阶段，若不存在则舍弃该解，进入新一轮的竞争决策，同时根据推论1 删除冗余结点。初始解越接近最优解，即初始解越好，求解速度就越快，可以通过设计合理的竞争规则和竞争力函数以及决策函数来得到较好的初始解。特别是在求解稀疏图的最大团问题时，竞争决策算法可以得到较好的初始解，同时根据推论1 快速删除较多冗余结点，实现快速求解。例如，1 个度小于等于2 的图，根据性质3 可知，该图的最大团最多只有3 个结点，竞争决策算法可以在资源分配阶段就能得到最优解，同时根据推论1 删除所有结点，问题得以快速求解。竞争决策算法原理简单，目前已经应用于TSP 问题(旅行商问题)、多目标TSP 问题、0−1 背包问题、最小顶点覆盖问题等，具有普遍的适用性。