基于马尔科夫过程的时间序列动态预测

曹子龙

摘 要：为了实现对设备状态的准确预测，本文对马尔科夫过程进行了分析和研究，基于设备状态量的在线监测时间序列实现动态预测，基于马尔科夫过程的动态预测相对于传统的预测方法可以大幅提高预测准确性，为实现准确的设备状态监测提供坚实依据。

关键词：基于马尔科夫过程；时间序列；动态预测

中图分类号：TP183 文献标识码：A 文章编号：1671-2064（2018）24-0241-02

0 引言

随着社会的经济社会的飞速发展，对各种工业设备、民用设备以及智能设备运行稳定性的要求越来越高，为了解决传统人工监测方法耗时长、准确性不高的问题，大量的在线监测传感器被应用到设备的状态监测中，利用在线监测传感器可以对设备的关键状态量（如：温度、压力、速度等）进行实时、准确的监测，进一步的，基于关键状态量可以实现设备状态的准确评价以及预测[1-2]。在线监测传感器在获取状态量时存在一个监测周期（如天、小时、秒等），在该监测周期内，获取实时数据，形成一个随着时间变化的状态量监测数列，该数列称为时间序列。现有的研究中，基于阈值比较方法，即将在线监测获取到的状态量数值与预设的阈值进行比较，通过判断是否超过阈值，来确定设备的状态[3]。另一方面，根据时间序列，通过挖掘时间序列中的内在特征和规律，预测该状态量在下一个时刻的数据，再通过阈值比较法，即可以知道下一个时刻的状态，从而实现对设备状态的预测。本文，基于马尔科夫过程挖掘设备状态量监测时间序列的特征，实现状态量的预测，并对传统方法进行改进，利用动态预测方法进一步提高预测准确率。

1.2 计算过程

对一个病例样本进行统计分析，假设样本中共有1万患者，为了治疗该病，有A和B两种药可以使用，且两种药的治疗周期就是一个月，即每患者每月用一种药，在将一种药全部用完之后再重新选择第一种或者二种药。在第一个月时，有3000患者使用A药，7000患者使用B药，而在实际使用中，使用A药的3000患者中，有60%的患者下月将继续使用A药，40%的患者将改用B要求；使用B药的7000患者中，有70%的患者下月将继续使用B药，30%的患者将改用A药。根据上述的信息可以得到A药与B药之间的转移概率矩阵为：

（7）

则，第二个月的时候分别使用A药和B药的人数为：（3000，7000）×=（3900，6100），继续预测第三个月的时候分别使用A药和B要的人数（3000，7000）××=（4170，5830），其中称为二步转移矩阵。

2 基于马尔科夫过程的时间序列预测

2.1 传统的马尔科夫预测过程

在传统的马尔科夫预测方法中，求取转移状态矩阵X，假设初始状态为P0，则下一个时刻为P1=X×P0，第n个时刻为Pn=An×P0。然而使用该种方法进行与测试，当n足够大的时候，Pn=Pn+1=Pn+2=……，造成预测不准确的问题[7-8]。

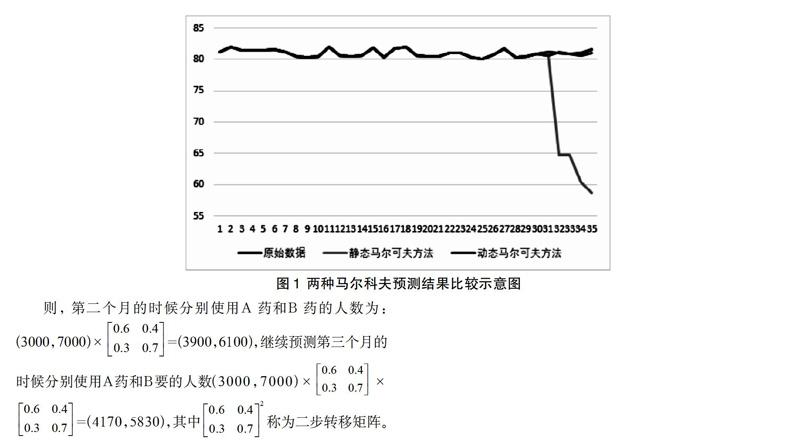
对于一个工业设备，通过监测其温度数据，可以实现设备状态的评估和预测。假设已经获取从第一天至第三十五天的数据，如图1黑色所示。采用第一种预测方法，利用前三十天的监测数据，根据马尔可夫理论，计算两两状态间的转移概率，生成状态转移矩阵。以第三十天温度所处的状态作为初始状态，进行多步状态转移，对后续五天的系统温度进行预测。预测结果如图1蓝线所示。由图中可以看出第三十一和第三十二天能够进行准确的预测，然而在第三十三到第三十五天时，预测值与实际值产生了较大的偏移。因此，使用传统的马尔科夫预测方法在进行较长时间的预测时，会出现较大的误差。

2.2 动态马尔科夫预测过程

为了改善传统马尔科夫预测过程中出现偏差较大的问题，本文提出了动态马尔科夫预测方法，以科夫传统方法的局限性。具体预测过程如下：使用第一天到第三十天的实际数据，预测第三十一天的预测数据；使用第二天到第二十九天的实际数據以及第三十一天的预测数据，预测第三十二天的预测数据；使用第二天到第二十八天的实际数据以及第三十一天和第三十二天的预测数据，预测第三十三天的预测数据。依次类推，直到预测到第三十五天的数据，预测结果如图中的红色曲线所示，由图中可以看出，基于动态马尔科夫预测方法预测的数据与真实值基本一致，准确率偏差小于3%。

3 结语

本文对马尔科夫过程进行了分析，对转移概率和转移概率矩阵进行了介绍。为了解决传统的马尔科夫过程在预测过程中的无法实现长期预测以及准确率不高的问题，本文提出了动态马尔科夫预测方法，从时间序列中动态选择样本集，利用动态迭代预测方法实现数据的预测。该方法可以广泛的应用在工业设备的在线监测中，实现对工业设备状态量的实时预测，进一步的，可以基于阈值判断法实现工业设备运行状态的判断。因为，本文所提方法具有广泛的实际意义。

参考文献

[1]胡文平，尹项根，张哲，等.电气设备在线监测技术的研究与发展[J].华北电力技术，2003（2）：23-26.

[2]张宇波.声音信号识别研究及在机械运行状态预测中的应用[D].湖南大学，2005.

[3]刘文萍，吴立德.图像分割中阈值选取方法比较研究[J].模式识别与人工智能，1997（3）：271-277.

[4]张玉芬，朱雅琳.马尔可夫性及其检验方法研究[J].价值工程，2012，31（2）：312-313.

[5]黄枫，吴纯杰.基于转移概率模型的老年人长期护理需求预测分析[J].经济研究，2012（s2）：119-130.

[6]唐小我，曾勇，曹长修.市场预测中马尔科夫链转移概率的估计[J].电子科技大学学报，1994（6）：643-648.

[7]吕颖钊，贺拴海.在役桥梁承载力模糊可靠性的马尔科夫预测[J].长安大学学报（自然科学版），2005，25（4）：39-43.

[8]严伟，钱育渝.马尔科夫预测在房地产市场营销中的应用研究[J].土木建筑与环境工程，2004，26（2）：110-115.