药学数据最优化问题的模型及算法

朱敏慧 陈娟 刘桂娟 王耀楠

摘 要：随着国家的发展与进步，医学发展越来越快，如何使得药物满足医学发展需要是目前我们要研究的重要课题。未来的药学研究逐渐倾向于多变量，非线性问题，而且研究药学数据优化的方法也越来越多，但大部分研究的结果都是不完善的。如何找到一种有效的方法求解药学数据优化模型变得越来越重要了。本文根据药学的适应性和多变性，建立了药物数据优化模型，针对模型提出了整数规划算法，进行数据实现，得到了药学数据最优值。

关键词：药物优化；最优化理论；药物费用

中图分类号：U491 文献标识码：A 文章编号：1671-2064（2018）24-0180-02

1 引言

国内外对药品的供应是不一致的，目前美国能够及时供应必须的药品，而我国正处于药学发展时期，药品供应不足，供药单位缺乏自动化制药设备，工作任务重，药品需求量大，而且药品库存量少[1-3]。医药产业风险高，费用高，收益高，新药的研发比较缓慢，虽然制药工业比较多，但是新药的制造十分有限，医药产业形式也比较严峻。这就要求我们需要努力提高新药的研发，我国药物发展自从1960年定量方法提出来以后，经过40多年的探索和努力，CADD已经成为一门先进的学科领域，提高了药物的研发过程，也为我国研制药物提供了新的思路。药物最优化研究是在20世纪40年代末[4-6]，Dantzig提出的单纯性方法，求解了一般线性规划问题，随着各种最优化问题：线性、非线性、多目标、整数规划等等各种优化方法的研究[7-8]，新方法不断出现，本文结合我国药学的发展，利用整数优化的理论，为促进药学方面的稳定发展，每种药品以整盒为单位，于是根据药学的数据特点，针对药物费用，建立了整数优化模型，并进行算法實现，提高了药品数据需求的分析。

2.1.4 拉格朗日区域割算法

初始：若x=1是不可行点，则无解，若u是可行点，则为P的最优解，停止。对原问题使用算法1得到最优解λ0和上界，求解松弛问题分别找到一个可行点和不可行点。

第一步；找一个最大的整数子箱子。

第二步：从整数子箱子中去掉可行解和非可行解所在的子集，缩小可行域的集合。并根据第一步寻求最优的可行点及不可行点代替初始的点。

第三步：若剖分后的整数箱子有更好的λ*和上界值，去掉，更新可行点及不可行点。

第四步：若整数箱子为空集，停止，找到一个最优解，否则，转第一步。

2.2 数据结果

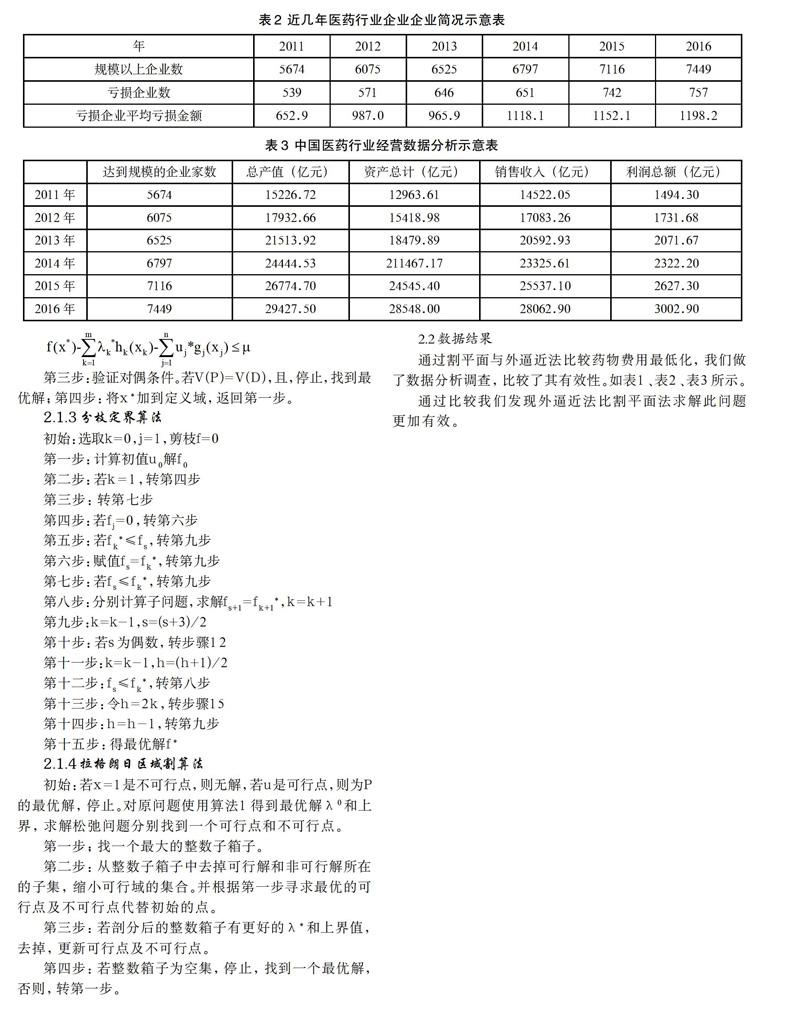
通过割平面与外逼近法比较药物费用最低化，我们做了数据分析调查，比较了其有效性。如表1、表2、表3所示。

通过比较我们发现外逼近法比割平面法求解此问题更加有效。

3 结语

当前针对药物的研究已经成为国内外的热门课题，因为药物研究的复杂性，患慢性，高费用等，使得我们必须深入对药学的学习，本课题利用整数最优化研究药物费用问题，比较全面，数据也易获取，更能节省较大的药物成本，该方法目前正广泛应用于药物数据模型中，方法相对有效。在今后的研究工作中，我们应该找到适合各种药物的最低费用模型，并对其实行完备算法，从而推动药物研究的更好发展。

参考文献

[1]许强.基本药物遴选的方法研究[D].武汉：华中科技大学，2011.

[2]郭宗儒.药物化学总论（第二版）.北京：中国医药科技出版社，2003.

[3]李春莲，王希诚，赵金城.应用改进型遗传算法进行药物分子对接设计.计算机工程与应用，2003，39（36）：31-33.

[4]Juan Chen， Guoqiang Wang. A new Primal-dual Interior-point Algorithm for CQSDO Based on A Finite Barrier.OMEE2011.2060-2063，厦门（EI收录）.

[5]陈娟，钱静静，刘常丽.多约束非线性整数规划的一种改进的算法.数学实践与认识，2011，41（23）：127-133.

[6]陈娟，刘桂娟，刘建波，冯增哲.基于整数规划的医疗卫生服务中心选址模型.数学实践与认识，2016，46（11）：292-295.

[7]农村卫生服务资源优化配置的DEA-Tobit两阶段法模型研究.数学实践与认识，45（5）：308-314.

[8]冯增哲，李晓梅，陈娟，刘建波，刘桂娟.城镇化后农村卫生服务站点选址的数学模型研究.数理医药学杂志，28（3）：317-318.