矩形隧道在抗震设计中的受力分析和计算

武好

摘 要：本文应用反应位移法，对某一矩形隧道在地震作用下的受力进行了分析，计算了矩形隧道结构周围各土层的动力弹簧刚度、地层位移，地震剪应力和结构惯性力，为隧道结构内力的有限元计算提供了输入参数，对地下结构的抗震设计具有一定的指导意义。

关键词：隧道；反应位移法；受力分析；抗震设计

中图分类号：U455.43 文献标识码：A 文章编号：1671-2064（2018）24-0096-02

0 引言

在科技快速发展、城市人口高度集中的今天，开发更大的城市空间已经成为城市可持续发展的必需条件，合理开发利用地下的空间既可以缓解地上空间资源的紧张，同时也可以加速城市结构的转型。因此，地下建筑（如地铁，地下管道，地下铁路等）在各个城市发展迅速，然而，在地下建筑兴建初期，人们对地下结构抗震防震性能的研究并未给予足够的重视。回顾近几年各国灾害案例，例如1995年日本阪神大地震时，有5个地铁车站和长约3km的隧道受到了严重的破坏，同时地铁调度系统失控，该事故造成巨大经济损失[1]。随着地下结构规模和数量逐渐增大，地下建筑的抗震设计引起了科研设计人员的高度关注。

目前，随着我国地下结构抗震设计理论的不断发展和提高，科研设计人员研究和总结出的一些实用的抗震分析方法也逐渐被纳入到规范条文中。在《地下铁道建筑结构抗震设计规范》和《城市轨道交通结构抗震设计规范》两个规范条文中就列出了多种地下结构抗震计算方法，包括惯性力法，反应位移法，反应加速度法和动力时程分析法等，其中，反应位移法是应用较为广泛的一种抗震设计方法[2]。本文使用反应位移法，针对某一矩形隧道进行抗震设计中的受力分析，以便工程人员参考。

1 隧道结构模型

某隧道为矩形的框架结构，结构宽25m，高15m。结构包括顶板，地板和侧壁。根据当地的土工资料，在地表50m时为基岩面，因此土体计算深度取50m，结构地板距离地表高度为25m，即结构顶板距离地面为10m，如图1所示。

该地区土层的物理性质如表1所示。

2 反应位移法

在进行地下结构抗震设计时，反应位移法将地下结构周围的土层用等效的弹簧来代替，土层位移直接施加在弹簧上，然后再加上结构所受到的惯性力和剪切力，进而进行结构的抗震计算。为此，需要确定动力弹簧刚度，底层位移，地震剪应力和结构惯性力四个参数。

2.1 动力弹簧刚度

动力弹簧刚度k（KN/m）计算公式为： （1）

式中，K为动力弹簧系数（KN/m3），L为不同土層弹簧间距（m），d为土层沿隧道与地下车站纵向的计算长度（m）。其中动力弹簧系数K根据日本铁路抗震设计规范进行求解[3]：

（1）顶板及底板，竖直弹簧系数和剪切弹簧系数按下式计算： （2）

（2）侧壁，水平弹簧系数和剪切弹簧系数按下式计算： （3）

式中，为土层动变形模量，为底板宽度，为侧墙高度。

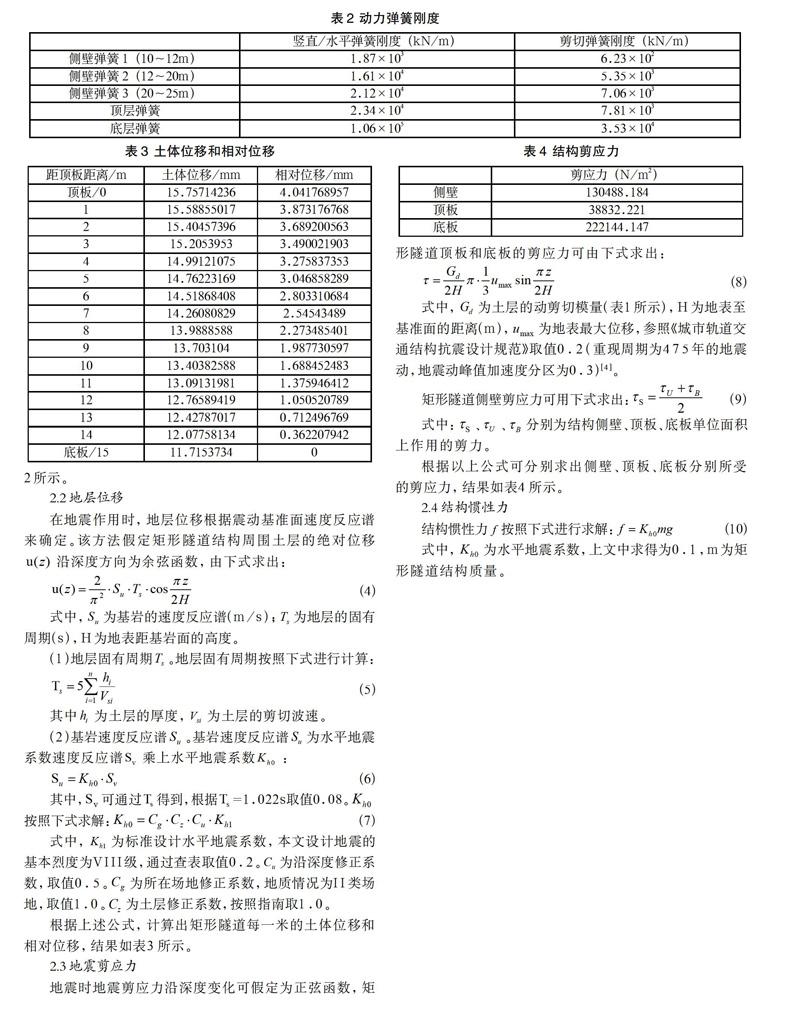
根据以上公式，该矩形隧道的五个动力弹簧刚度如表2所示。

2.2 地层位移

在地震作用时，地层位移根据震动基准面速度反应谱来确定。该方法假定矩形隧道结构周围土层的绝对位移沿深度方向为余弦函数，由下式求出：

（4）

式中，为基岩的速度反应谱（m/s）；为地层的固有周期（s），H为地表距基岩面的高度。

（1）地层固有周期。地层固有周期按照下式进行计算：

（5）

其中为土层的厚度，为土层的剪切波速。

（2）基岩速度反应谱。基岩速度反应谱为水平地震系数速度反应谱乘上水平地震系数：

（6）

其中，可通过得到，根据=1.022s取值0.08。按照下式求解： （7）

式中，为标准设计水平地震系数，本文设计地震的基本烈度为VIII级，通过查表取值0.2。为沿深度修正系数，取值0.5。为所在场地修正系数，地质情况为II类场地，取值1.0。为土层修正系数，按照指南取1.0。

根据上述公式，计算出矩形隧道每一米的土体位移和相对位移，结果如表3所示。

2.3 地震剪应力

地震时地震剪应力沿深度变化可假定为正弦函数，矩形隧道顶板和底板的剪应力可由下式求出：

（8）

式中，为土层的动剪切模量（表1所示），H为地表至基准面的距离（m），为地表最大位移，参照《城市轨道交通结构抗震设计规范》取值0.2（重现周期为475年的地震动，地震动峰值加速度分区为0.3）[4]。

矩形隧道侧壁剪应力可用下式求出： （9）

式中：、、分别为结构侧壁、顶板、底板单位面积上作用的剪力。

根据以上公式可分别求出侧壁、顶板、底板分别所受的剪应力，结果如表4所示。

2.4 结构惯性力

结构惯性力按照下式进行求解： （10）

式中，为水平地震系数，上文中求得为0.1，m为矩形隧道结构质量。

3 结语

本文以矩形结构的隧道为研究对象，采用反应位移法这一地下结构抗震设计的基本方法，对该结构在地震动荷载作用下的受力情况进行了分析，求解了各土层的动力弹簧刚度、结构各位置的地层位移、地震剪应力及整体结构的惯性力。在此基础上，相关设计人员可通过这些参数选择隧道结构的材料，进而进行有限元计算，求出结构所受的内力。由于本文将地下土层简化为规则分布的均匀土层，未来可以针对混合土层下矩形隧道的受力进行进一步分析和研究。

参考文献

[1]邓宇洁，梁发云.地下结构地震反应规范计算方法的对比分析[J].地震工程学报，2018，40（5）：996-1003.

[2]郑学涛.基于反应位移法某地铁车站抗震研究[D].石家庄铁道大学，2015.

[3]施有志，华建兵，李秀芳，林树枝.反应位移法在地下综合管廊抗震设计中的应用[J].吉林大学学报（地球科学版），2018，48（6）：1785-1796.

[4]GB50909-2014.城市轨道交通结构抗震设计规范[S].北京：中国计划出版社，2014.