关于一类多目标半无限分式规划的最优性条件
2018-02-21严建军李江荣
严建军,李 钰,李江荣,杨 帆
(1.延安职业技术学院, 陕西 延安 716000; 2.延安大学 数学与计算机科学学院,陕西 延安 716000)
随着多目标最优化和半无限规划的研究发展,凸性理论逐步被广泛地应用到各个研究范畴中,且取得了许多有意义的重要成果。文献[1]引入了(F,α,ρ,d)-凸函数,文献[2]对之推广,得到了(C,α,ρ,d)-凸函数,并研究了涉及这类凸性的最优性条件和对偶结果。文献[3-7]对于涉及(C,α,ρ,d)-凸性的多目标规划、多目标分式规划等问题的最优性和对偶理论进行了研究。受此启发,结合局部Lipschitz函数、局部渐近锥K、K-方向导数和K-次微分,提出了一类广义(C,α,ρ,d)K,θ-凸函数等凸性概念,并在新的广义凸性下,研究了一类多目标半无限分式规划的最优性条件。
1 基本概念
本文均假设X⊂Rn且非空。
定义1 称函数f∶X→R是局部Lipschitz的,若∀z∈Rn,∃k>0与U(z),对∀x,y∈U(z),有
|f(x)-f(y)|≤k||x-y||
定义2[2]称函数C∶X×X×Rn→R在Rn上关于第3个变元是凸的,若∀(x,x0)∈X×X,∀y1,y2∈Rn,有
C(x,x0)(λy1+(1-λ)y2)≤λC(x,x0)(y1)+
(1-λ)C(x,x0)(y2),∀λ∈(0,1)
本文均假设∀(x,x0)∈X×X,有C(x,x0)(0)=0。
定义3[2]设函数f∶X→R是局部Lipschitz函数,若∃α∶X×X→R+{0},ρ∈R,d∶X×X→R+,如果对∀x∈X,有
[f(x)-f(x0)]/α(x,x0)≥C(x,x0)(ξ)+
ρd(x,x0)/α(x,x0), ∀ξ∈∂f(x0)
则称函数f在x0处是(C,α,ρ,d)-凸函数。

bi(x,x0)φ[fi(x)-fi(x0)]≥αi(x,x0)C(x,x0)(ξi)+
ρid2(θi(x,x0)), ∀ξi∈∂Kfi(x0)
则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-凸函数。
如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-凸函数,则称f在X上是广义(C,α,ρ,d)K,θ-凸函数。

bi(x,x0)φ[fi(x)-fi(x0)]<0⟹αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))<0,∀ξi∈∂Kfi(x0)
则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-伪凸函数。
如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-伪凸函数,则称f在X上是广义(C,α,ρ,d)K,θ-伪凸函数。
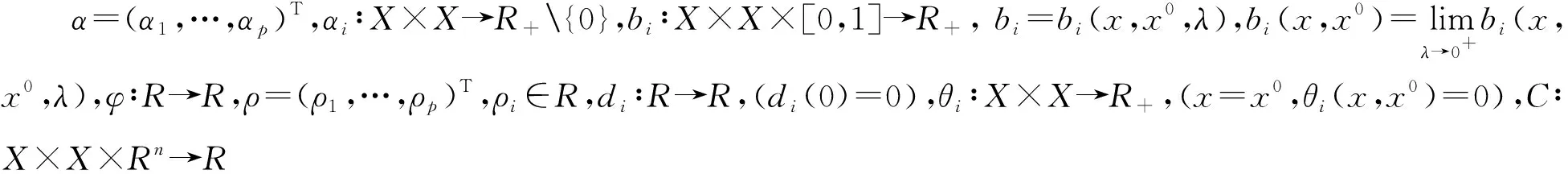
bi(x,x0)φ[fi(x)-fi(x0)]≤0⟹
αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))<0,
∀ξi∈∂Kfi(x0),
则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-严格伪凸函数。
如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-严格伪凸函数,则称f在X上是广义(C,α,ρ,d)K,θ-严格伪凸函数。
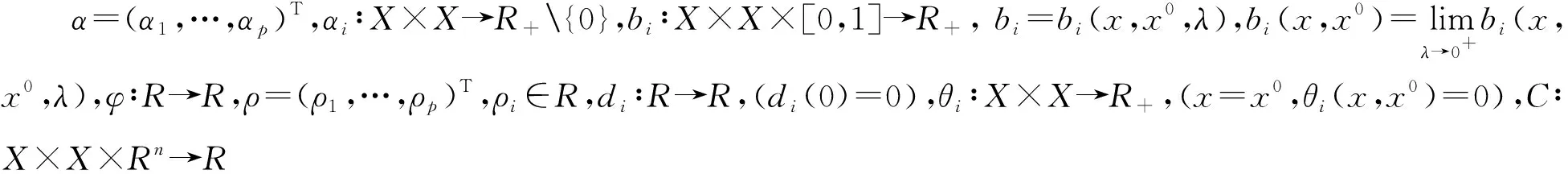
bi(x,x0)φ[fi(x)-fi(x0)]≤0⟹
αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))≤0,
∀ξi∈∂Kfi(x0)
则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-拟凸函数。
如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-拟凸函数,则称f在X上是广义(C,α,ρ,d)K,θ-拟凸函数。
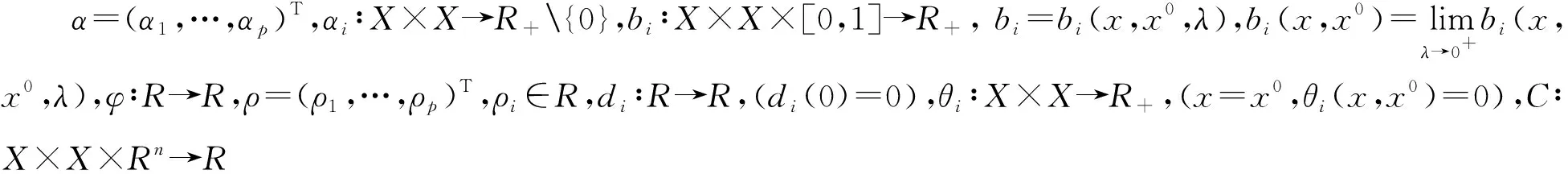
bi(x,x0)φ[fi(x)-fi(x0)]<0⟹
αi(x,x0)C(x,x0)(ξi)+ρid2(θi(x,x0))≤0,
∀ξi∈∂Kfi(x0),
则称函数f=(f1,…,fp)在x0∈X处是广义(C,α,ρ,d)K,θ-弱拟凸函数。
如果函数f在X上每一点处为广义(C,α,ρ,d)K,θ-弱拟凸函数,则称f在X上是广义(C,α,ρ,d)K,θ-弱拟凸函数。
注1 若K取Clarke切锥,设C(x,x0)(ξ)=F(x,x0;ξ),α(x,x0)=1,ρ=0,则在本文中提出的广义(C,α,ρ,d)K,θ-凸函数等即为文献[13]中的一致Fb-凸函数等。
注2 若K-次微分取通常意义下梯度,设d2(θ(x,x0))=d(x,x0),φ(a)=a,b(x,x0)=1,则本文提出的广义(C,α,ρ,d)K,θ-凸函数即为定义3。
2 主要结果
考虑多目标半无限分式规划:
本文均记:



注3 每个有效解是弱有效解,反之不成立。

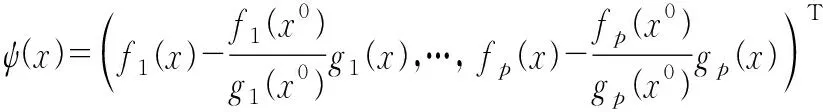
②h(x)在x0处是广义(C,β,ρ2,d)K,θ-拟凸函数;

④α1=…=αp=β1=…=β(J)=δ;
⑤b1(x,x0)>0,b2(x,x0)>0;
若a≤0,则φ1(a)≤0;若a≤0,则φ2(a)≤0;

则x0是(MSFP)的有效解。
证明若x0不是(MSFP)的有效解,则∃x∈X,使得
ψ(x)≤ψ(x0)
至少存在一个k,1≤k≤p,有
ψk(x)<ψk(x0)
由条件(v)和(i)知对i=1,…,p有
b1i(x,x0)φ1(ψi(x)-ψi(x0))≤0⟹
αi(x,x0)C(x,x0)(ξi)+ρ1id2(θi(x,x0))<0,
∀ξi∈∂Kψi(x0)
因λ0∈Λ+,则有
(1)
由hj(x)≤0,hj(x0)=0,j∈J(x0)知
hj(x)≤0=hj(x0)
由条件②和⑤,有
b2j(x,x0)φ2(hj(x)-hj(x0))≤0⟹
βj(x,x0)C(x,x0)(ζj)+ρ2jd2(θj(x,x0))≤0,
∀ζj∈∂Khj(x0)

∀ζj∈∂Khj(x0)
(2)
因此
(3)
而式(1)与式(2)相加,并利用函数C的凸性和条件④,有
由条件⑥,有
上式与式(3)矛盾,故x0是(MSFP)的有效解。

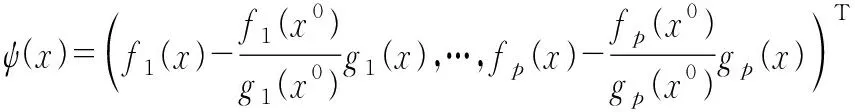
②h(x)在x0处是广义(C,β,ρ2,d)K,θ-拟凸函数;
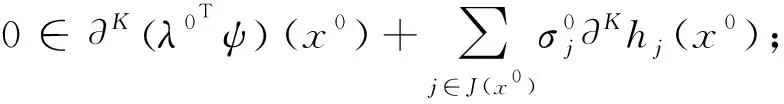
④α1=…=αp=β1=…=β(J)=δ;
⑤b1(x,x0)>0,b2(x,x0)>0;
若a<0,则φ1(a)<0,且φ1(0)=0; 若a≤0,则φ2(a)≤0;

则x0是(MSFP)的弱有效解。
证明若x0不是(MSFP)的弱有效解,则∃x∈X,使得
ψ(x)<ψ(x0)
由条件①和⑤知对于i=1,…,p,有
b1i(x,x0)φ1(ψi(x)-ψi(x0))<0⟹
αi(x,x0)C(x,x0)(ξi)+ρ1id2(θi(x,x0))<0,
∀ξi∈∂Kψi(x0)
因λ0∈Λ,则有
(4)
由hj(x)≤0,hj(x0)=0,j∈J(x0)知
hj(x)≤0=hj(x0)
由条件⑤,有
b2j(x,x0)φ2(hj(x)-hj(x0))≤0⟹
βj(x,x0)C(x,x0)(ζj)+ρ2jd2(θj(x,x0))≤0,
∀ζj∈∂Khj(x0)

∀ζj∈∂Khj(x0)
(5)
因此
(6)
而式(4)与式(5)相加,并利用函数C的凸性和条件④,有
由条件⑥,有
上式与式(6)矛盾,故x0是(MSFP)的弱有效解。
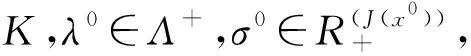
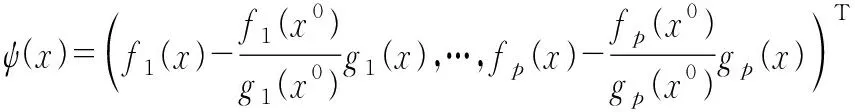
②h(x)在x0处是广义(C,β,ρ2,d)K,θ-严格伪凸函数;

④α1=…=αp=β1=…=β(J)=δ;
⑤b1(x,x0)>0,b2(x,x0)>0;
若a≤0,则φ1(a)≤0; 若a≤0,则φ2(a)≤0;

则x0是(MSFP)的。
证明与定理1的证明类似。
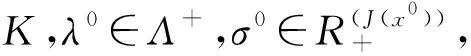
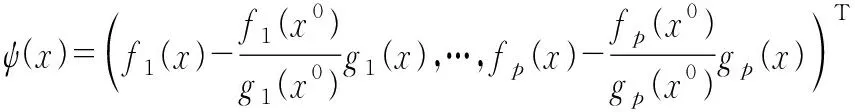
②h(x)在x0处是广义(C,β,ρ2,d)K,θ-严格伪凸函数;
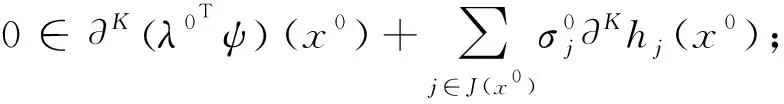
④α1=…=αp=β1=…=β(J)=δ;
⑤b1(x,x0)>0,b2(x,x0)>0;
若a<0,则φ1(a)<0,且φ1(0)=0; 若a≤0,则φ2(a)≤0;

则x0是(MSFP)的弱有效解。
证明与定理2的证明类似。
类似可得以下定理:
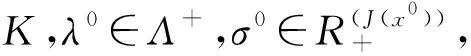

②h(x)在x0处是广义(C,β,ρ2,d)K,θ-拟凸函数;
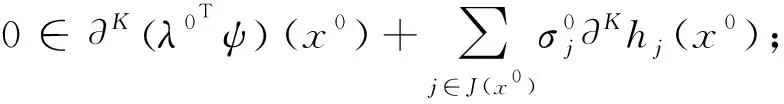
④α1=…=αp=β1=…=β(J)=δ;
⑤b1(x,x0)>0,b2(x,x0)>0;
若a<0,则φ1(a)<0,且φ1(0)=0; 若a≤0,则φ2(a)≤0;

则x0是(MSFP)的有效解。
3 结束语
本文提出一类新的广义凸函数概念,研究了涉及这些新广义凸性的一类多目标半无限规划的最优性,所得结果从理论上对已有凸性进行了推广,充实了广义凸性和多目标半无限规划的相关理论,可进一步深入研究与之相关的对偶性、鞍点等内容。
