基于MAHP的作战油料调运优化模型及应用
2018-02-21郁鹏飞周庆忠
郁鹏飞,周庆忠,熊 彪,孙 涛
(中国人民解放军陆军勤务学院, 重庆 401311)
油料调拨运输是作战油料保障的一个重要环节,其效率的高低将直接影响保障效果。战时油料前送保障通常要保障多个方向、多个地域、多个地点,战场环境的复杂性决定必须将油料保障力量小型化、模块化分组,按照“合成、混编、超常”的要求,编成若干功能完善、机动性强的油料保障分队,利用发达的交通网,对各作战部队实施快速、灵活、精确的前送支援保障[1]。战时一旦多个作战部队同时提出补给需求,如何在短时间内制定油料调拨运输方案,作出最佳保障策略,对油料保障行动起着至关重要的作用。
油料调拨运输优化的方法有很多,赖伟等[2]提出将熵权法应用于对作战油料公路运输路线的优化选择;苏涛等[3]利用改进的最短路径算法对最安全运输路线进行求解;闫华等[4]采用粒子群算法对带有时间窗约束下的油料调拨运输进行优化求解;李开红等[5]利用匈牙利算法对油料调度进行优化研究;王耀等[6]建立双层规划模型对油料运输网络进行优化,选择最优运输路径。上述模型和方法从不同方面分别研究了战时油料保障的各个环节,但对于前送保障这种末端保障没有综合考虑安全性、时效性等多目标优化,对于运输影响因素权重的确定也多是根据经验确定,缺乏一套科学的理论方法。本文旨在基于改进层次分析法的科学理论方法,合理地确定各运输影响因素的权重值,对油料运输中路径寻优和任务指派的多目标优化问题进行建模分析,从而得出运输最优路线及任务指派方案,为后勤指挥员提供可靠的参考方案,起到辅助决策的作用。
1 油料运输路径优化模型的构建
油料运输“成本”在不同部门、时期、情况下其影响因素及权重有所不同,这些因素往往是模糊抽象的,不易准确把握,而不同影响因素权重的科学、合理确定通常决定了运输模型的优化能力。本文借助于改进的层次分析法(MAHP)来确定各因素的指标权重,以提高指标权重的可信度,为建立有效的路径优化模型奠定基础。
1.1 改进层次分析法(MAHP)
传统的层次分析法(AHP)在确定指标权重时,需要由专家对每一个指标两两进行1~9的比例标度量化,这种方法需要消耗大量时间,同时在战时情况下油料输送中各指标的相关量化标度不确定性较大[7],而且也不需要对指标对比如此精确,各指标之间的相对量化优先值往往是最贴合实际的数据。因此,本文结合运输实际情况提出的改进层次分析法(MAHP),通过建立优先关系矩阵的方式,对比得出各因素之间的相对量化层次,用以替代1~9比例标度量化方法,进而实现决策由定性向定量的转化,不仅能够准确地反映决策因素的不确定性,同时又能避免标度量化的繁琐细节,提高决策的效率和决策结果的可信度。
假设油料运输影响因素集为X,有
X={x1,x2,…,xn}
其中xj为第j个指标,j=1,2,…,n为影响因素个数。
1) 建立优先关系矩阵X=(xij)n×m,
式中g(i)和g(j)分别表示指标xi和xj的相对重要程度。
2) 将优先关系矩阵X转化为模糊一致矩阵R
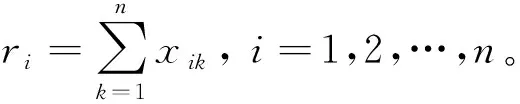

经过这种方法建立的判断矩阵可以保证模糊一致性。
3) 指标权重计算
对模糊一致判断矩阵每行元素求和:
不含对角线元素之和:
由于li表示指标i相对于上层目标的重要程度,因此对其归一化可得各指标权重:
Wi=li/∑li=2l/n(n-1)
1.2 实例应用
假设油料运输“成本”影响因素主要包括运输费用x1、安全x2、时间x3、距离x4等因素[8]。下面根据对各指标的要求,用MAHP确定其在路径优选模型中的权重。建立关系矩阵X=(xij)4×4n=4(见表1),将X转变为模糊一致矩阵R=(rij)4×4(见表2),计算得出各指标权重值,见表3。
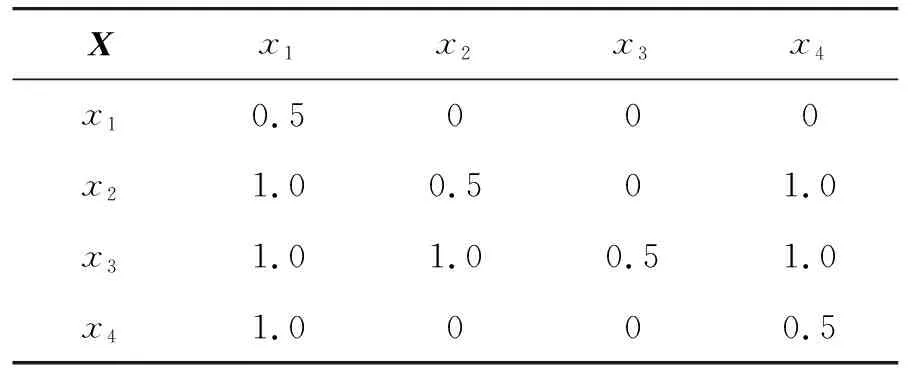
表1 优先关系矩阵X
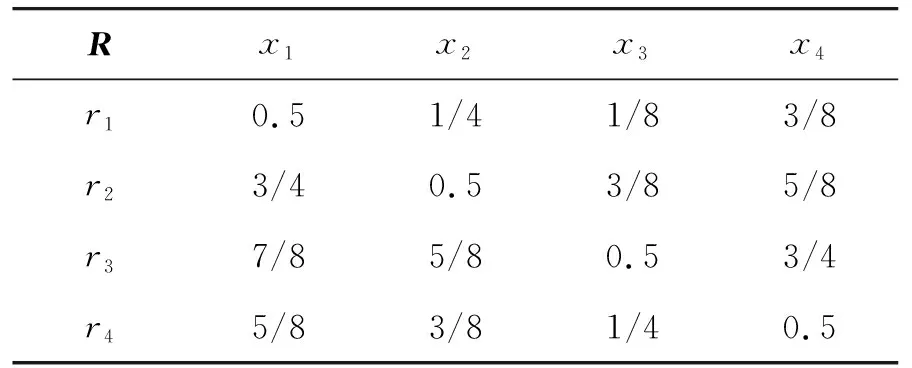
表2 模糊一致矩阵R

表3 各指标权重分配表
运用上述方法,各级指挥员能够在短时间内按照任务要求对各影响因素进行直观的分析,能快速建立优先关系矩阵,进而求出客观、有效的各指标权重值,最大限度地保证作战油料保障的时效性。
1.3 油料运输路径寻优模型构建
1) 道路权值计算
据上述分析可知,运输影响因素的参数矩阵:
Xij=[(xk)1×n]ij,k=1,2,3,…,n
各因素权重矩阵:
Wij=[(wk)n×1]ij,k=1,2,3,…,n
道路节点i和j之间的运输“成本”Cij可表示为:
Cij=Xij×Wij
2) 模型构建
引入0~1变量xij,X={xij|(i,j)∈V)}代表一条保障路径。

约束方程:

2 油料运输任务指派优化模型
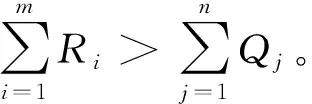
1) 目标函数
涉及整体的调度问题时,应考虑单条路径的油料运输量以及方案整体的最优化。假设每辆运油装备容量h都相同,各需求点的需求量Qj以运油车数量D表示,则模型目标方程可表示为:
式中:Gij表示保障点i到需求点j最优路线的运输“成本”;Dij表示保障点i对需求点j的保障数量。
2) 约束方程
① 需求量约束,保证各需求点的需求量能够得到满足。
② 保障能力约束,保证各保障点的保障量不能超过自身储备量。
综上所述,油料运输任务指派优化模型为:

3 实例模拟仿真
在某作战地域,合成第×旅担任对×××地域的进攻作战任务,在前沿阵地编组为5个攻击群进行作战。勤务支援营在后勤配置地域开设战术野战油库对各攻击群进行油料前送保障,联勤保障力量在相应地域开设战役野战油库,并抽组形成3个油料保障分队对旅战术野战油库、各攻击群进行支援保障,具体战场油料保障模式如图1所示。
考虑运输时间、运输安全、运输距离作为运输“成本”的影响因素,将道路交通网络转化为数学网络模型,如图2所示。
图2中:点1、2、3代表战役油料保障分队;6代表旅战术野战油库;11、12、13、14、15代表攻击群;其余各点表示道路中转点;每条线路上的数值分别代表连接两个端点路线的运输距离S、安全通过率差值(1-P)、运输时间T。已知各保障分队及油库的保障能力及各个攻击群的油料需求量。决策人员根据现地情况及要求,对3类指标按照GAHP法确定权重为W=[0.25,0.4,0.35]。
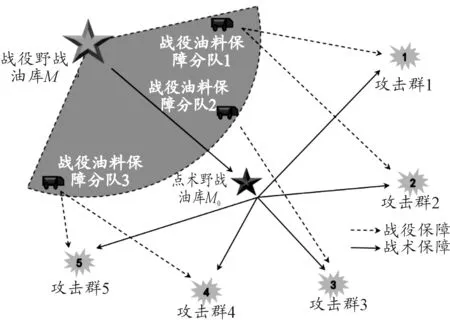
图1 合成旅战场油料保障模式
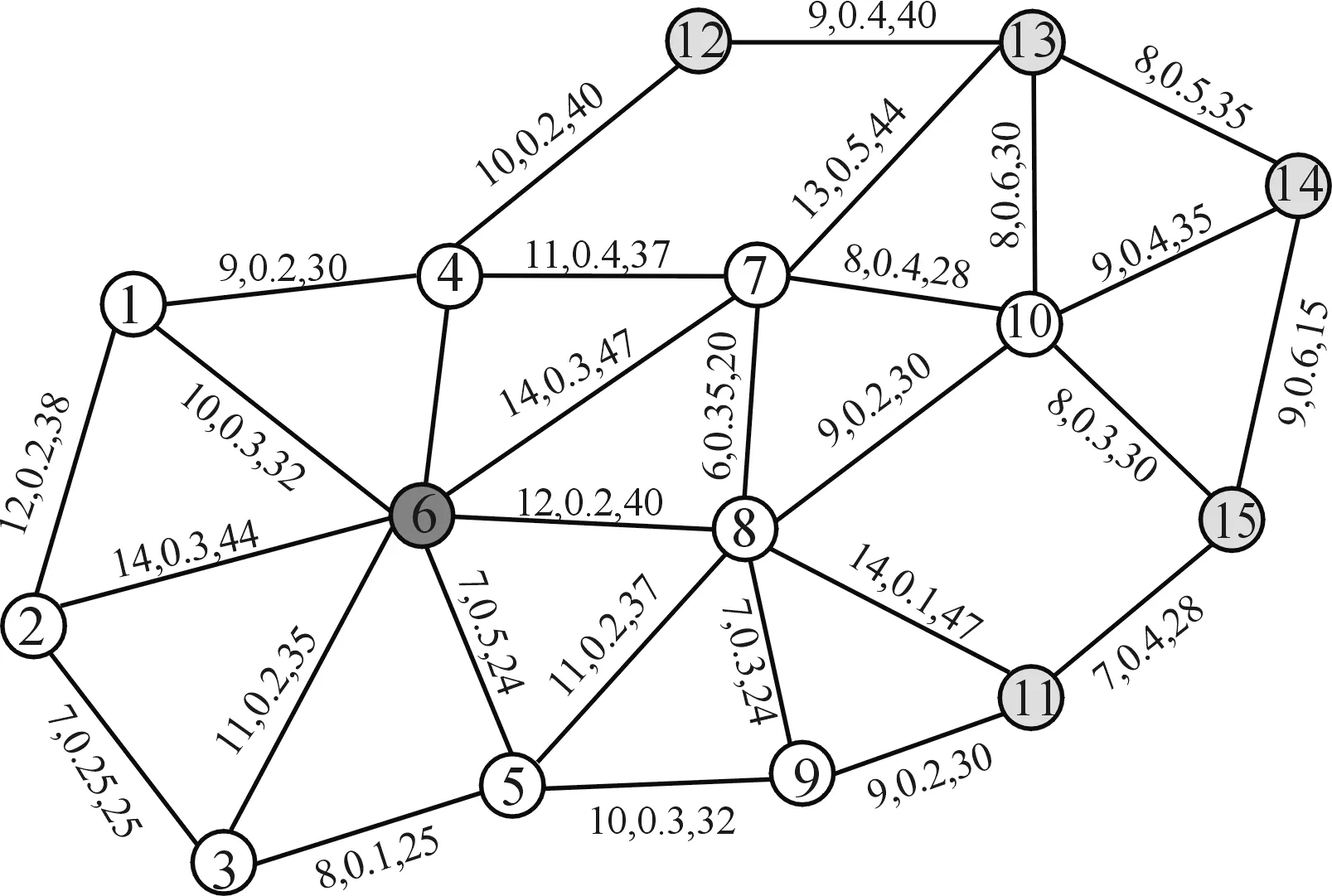
图2 作战区域交通网络模型
首先,从图2得到补给点和油料需求点之间道路连通情况,并用矩阵X表示连通的道路情况,其中元素的下标表示道路连接点标号。
由图2网络图中数据可知:任意两个端点路线的运输距离S最大值为14,安全通过率差值(1-P)最大为1,运输时间T最大值为47。因此,令S=MAX{Sij}=14,C=MAX{Tij}=47,对矩阵X进行归一化处理,得到X′,进而得出“成本”系数矩阵C为
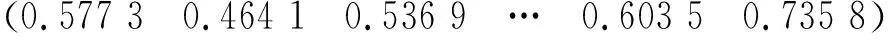
其次,根据“成本”系数矩阵C,将原交通网络模型简化,如图3所示。
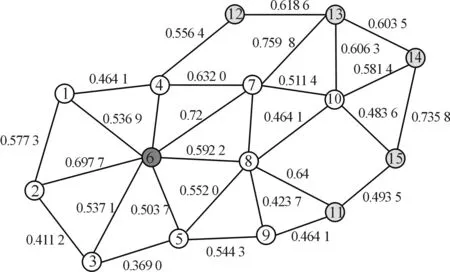
图3 道路运输“成本”系数示意图
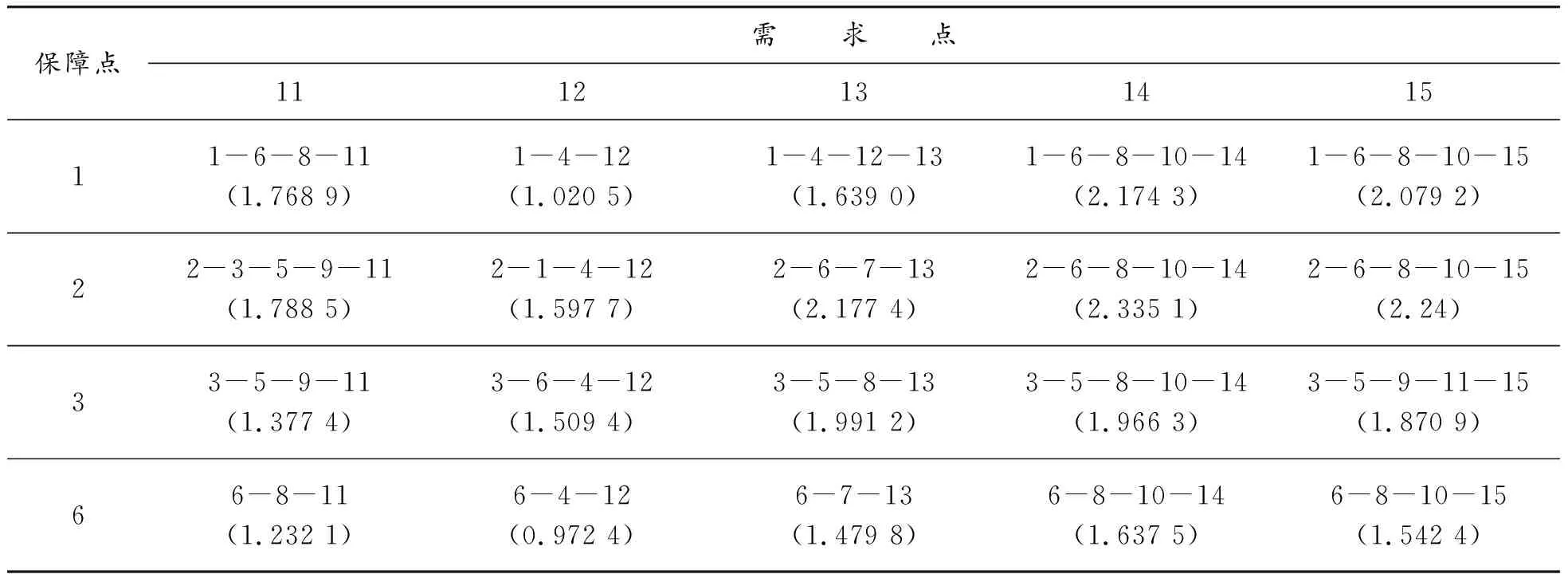
再次,根据图3各条道路运输“成本”系数,采用D算法,借助于Matlab软件进行编程求解[9],得到各个油库补给点到各攻击群的最优化线路,如图4及表1所示。
关键程序代码:
S=[数据];E=[数据];W=[数据];
G=sparse(S,E,W);
G(15,15)=0;
P=biograph(G,[],′ShowWeights′,′on′);
H=view(P);
[Dist,Path]=graphshortestpath(G,1,15,′Method′,′Dijkstra′)
set(H.Nodes(Path),′Color′,[1 0.4 0.4]);
edges=getedgesbynodeid(H,get(H.Nodes(Path),′ID′));
set(edges,′LineColor′,[1 0 0]);
set(edges,′LineWidth′,2.0);
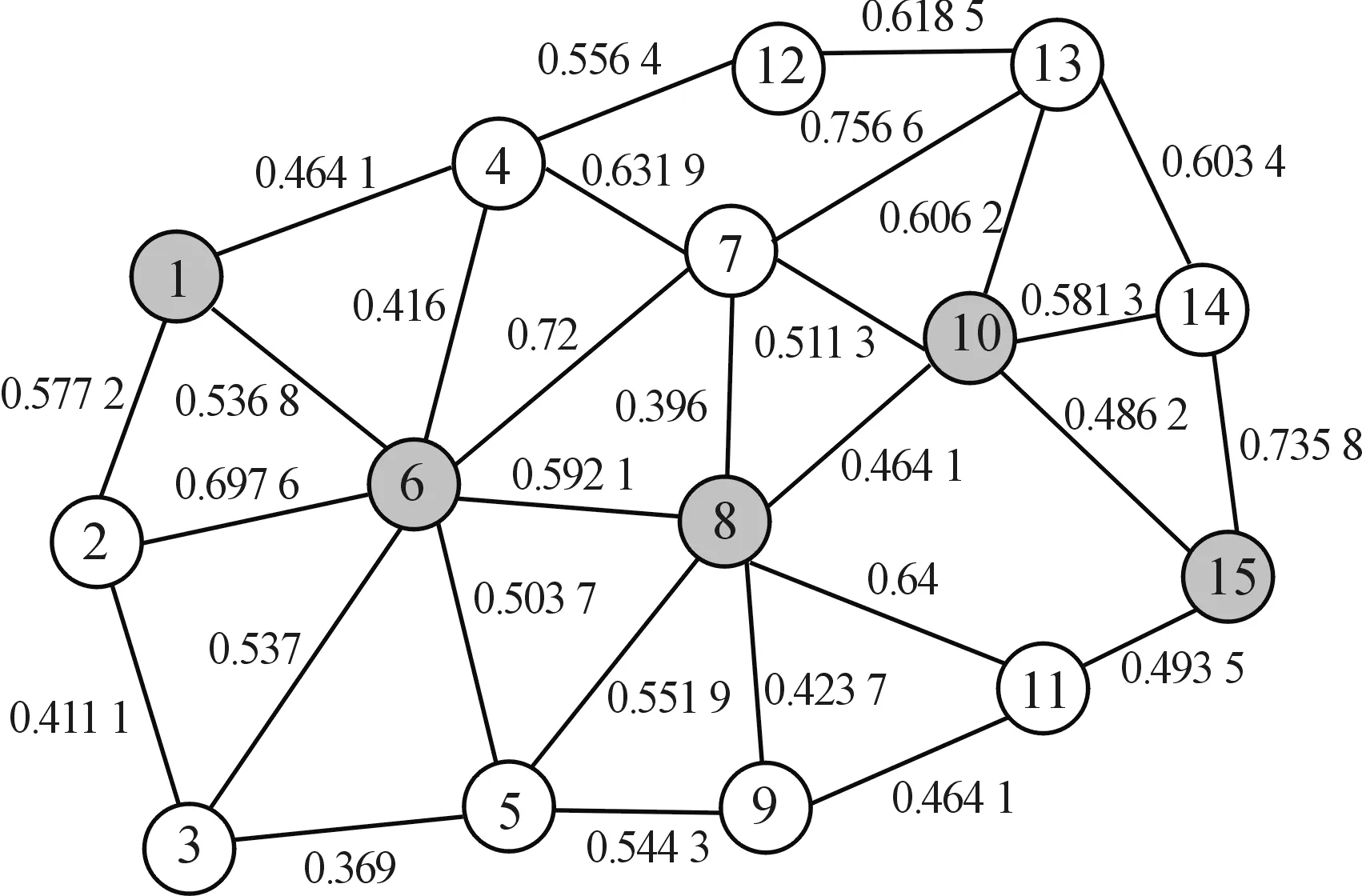
图4 求解最优路线
保障点需 求 点111213141511-6-8-11(1.768 9)1-4-12(1.020 5)1-4-12-13(1.639 0)1-6-8-10-14(2.174 3)1-6-8-10-15(2.079 2)22-3-5-9-11(1.788 5)2-1-4-12(1.597 7)2-6-7-13(2.177 4)2-6-8-10-14(2.335 1)2-6-8-10-15(2.24)33-5-9-11(1.377 4)3-6-4-12(1.509 4)3-5-8-13(1.991 2)3-5-8-10-14(1.966 3)3-5-9-11-15(1.870 9)66-8-11(1.232 1)6-4-12(0.972 4)6-7-13(1.479 8)6-8-10-14(1.637 5)6-8-10-15(1.542 4)
最后,假设各油料保障分队保障能力及各攻击群需求量见表2;采用匈牙利算法[10]借助Matlab进行编程求解可快速得出任务指派优化方案,见表3。
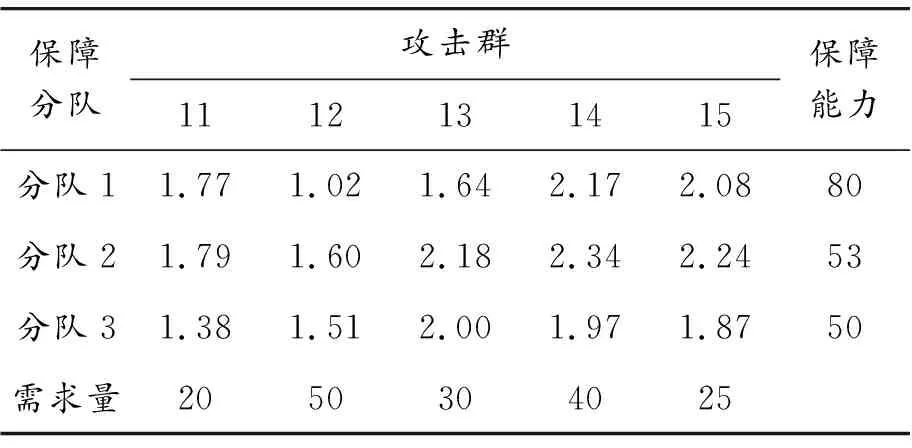
表2 各保障分队保障能力与攻击群需求数据

表3 任务指派优化方案
根据表3制定出油料保障任务优化方案为:保障分队1对攻击群12、13分别保障50、30 t油料;保障分队2对攻击群14保障35 t油料;保障分队3对攻击群11、14、15分别保障20、5、25 t油料,达到在保障成本最小、各保障分队保障能力范围内,各攻击群需求量均得到满足的目的。
4 结束语
本文对油料保障环节中的运输路径和任务指派优化问题进行了建模分析。引入改进的层次分析法(MAHP)建立优先关系矩阵,确定影响运输“成本”各因素的权重,将多目标运输优化问题转化为类似于单一“成本”因素的最短路径问题,并建立路径优化模型和任务指派优化模型。对模型进行实例模拟仿真并借助Matlab求解验证。结果表明:所建模型能快速、准确地确定最佳运输路径,形成科学合理的任务派遣方案,对辅助作战油料保障决策具有较高的参考价值。
