谈试卷评讲课中一题多解与一题多问多变的重要性

广东省英德市英德中学 郭建国

考试是数学教学的一个重要组成部分，是评价的重要工具之一，是检测教学效果的有效手段，也是学生阶段性查漏补缺的一次好机会。考试目的的最终价值体现在于学生对数学系统知识体系的“悟”，学生的“悟”很大程度上离不开教师的“评”。

试卷评讲是教学中的一个不容忽视的重要环节，其教学技术含量甚至高于对新课的讲授，故试卷评讲课务必有策略地进行。一张试卷该如何评讲，不同的教师会采用不同的方法，即使是同一个教师也会因为题型、错因、试题的难度、考情等的不同而会采取不同的方式和方法。但是，怎样才能收到更好的效果？针对此困惑，我做了一些尝试。

我毕业参加工作的前三年里，试卷评讲课上基本上是对整张试卷逐题讲解，但没有做针对性分析，没有进行归纳总结，最终发现这样的试卷评讲课其实效果不好，一周后，重新考类似的题，甚至考一样题，当时做错的学生中大部分人还会再次做错，因为这部分学生还是没有对此部分的数学知识体系进行系统的建构好，即学生的思维意识形态里只是有这部分数学知识的碎片而已，似曾相识却又不知从何做起，从而一错再错。 由此，我认真备课，力求面面俱到，将考试中考察的知识点逐一讲透，事实上，时间是不允许的，再者，教师一手包办的填鸭式教学方式培养出来的学生还是不能自主灵活地解决复杂多变的数学问题。 基于以上尝试和考虑，我认为试卷评讲课中，包括复习课，应突出重点，细讲难点，通过一题多解、一题多问多变的教学手段，以点带面，把重点、主干知识完整系统地讲清，让学生悟透。

下面通过举例来说明：

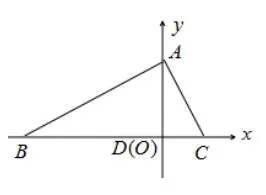
例1,如图，在ΔABC中,AB=BC= 3,∠ABC= 3 0°,AD是BC边上的高,则的值等于.

方法一：(线性运算)

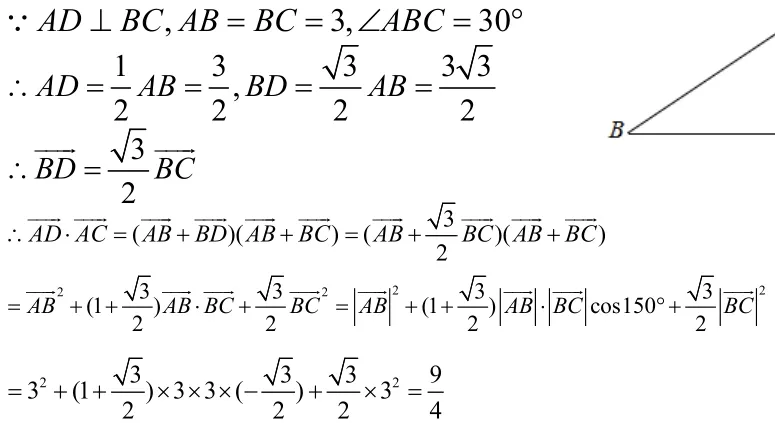
方法二：(向量投影的妙用)

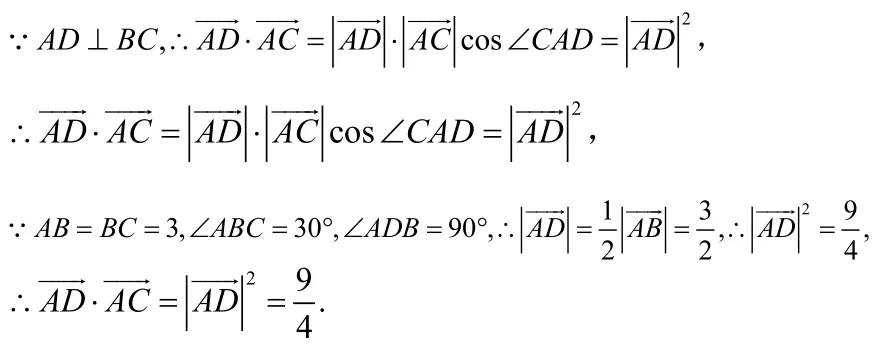
方法三：(向量的坐标法)

如右图所示，以D为原点建立平面直角坐标系O-xy，

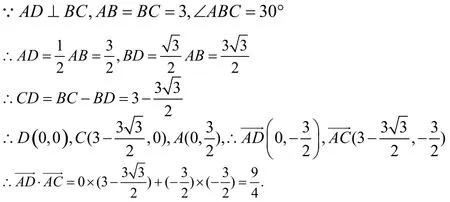
例2，已知x、y≥0且x+y=1,求x2+y2的取值范围.

方法一：换元法(三角换元)

∴当cos4α=-1时，取x2+y2最小值为,当cos4α =1时，x2+y2取最大值为1.

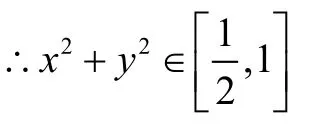
方法二：换元法(对称换元)

解：∵x、y≥0且 1,x+y=∴设其中∴ 当t=0时 ，x2+y2取最小值为,当t=±时，x2+y2取最大值为1.

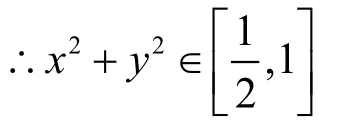
方法三：函数法

解 ： ∵x、y≥0 且∴x对称轴

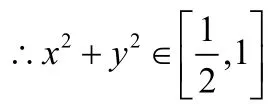
方法四：几何法

解：∵x、y≥0且x+y= 1 ,∴设点p(x,y)到原点的距离为

当OC⊥AB取得最小值，

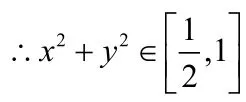
方法五：不等式法

解：∵x、y≥0且 1,x+y=∴当xy=0时，取得x2+y2最大值为1，时，取得最小值为

当

通过“一题多解”的教学活动激励学生“联想、猜想”方面讨论来逐步培养学生数学的发散性思维，对于一道题的分析，因考虑的角度不同，而得到不同的解法及解题依据，这是一题多解的特点，从而对基础知识有效地复习，在解题过程中激发思维火花，培养了学生探索和解决问题的能力。但是一题多解的最终目的是要寻找一种最优、最简便的方法，也就是说一题多解的目的是为了拓广思维力度，还能起到一个复习各种知识，事半功倍地提高解题能力的目的，同时，从上两例中我们可以看到数学思想方法的多样性。

从对“一题多解”的探讨，我们还可联想到教学中的一题多问和一题多变。一题多问的主要目的是培养学生全面地看待问题，而一题多变的主要目的是帮助学生对新的数学知识点形成一个共同的认知体系。下面通过举例来进一步说明：

(1).求a1+a2+··+a6+a7的值.

(2).求a0+a2+a3+a4+a5+a6+a7的值.

变式2：

(1).求a0+a1+a2+···+a10的值.

(2).求a1+a2+···+a10的值.

例4，已知a＞0,b＞0,a+b=2,则的最小值是______．

变式1：已知a＞ 0 ,b＞ 0 ,a+ 2b= 1 ,则2a+ 4b的最小值是______．

变式2：已知a2+2b2= 5 ,则的最大值是_____

变式3：已知a+b= 2 ,b＞ 0 ,则当a= _ ___时,取得最小值.

一题多问多变是通过提供问题的背景，对题目进行引申、变化和发散，进而归纳总结一类甚至几类问题间的逻辑关系。经过学生讨论、交流，教师点拨，让学生发现：改变题目的条件会导出什么结论，保留题目的条件，改变问题又应该如何处理，条件做类似变换，结论能否扩大到一般等等，像这样富有创造性的全方位思考，常常是学生对新的数学知识体系进行有效建构的突破口。

随着素质教育的层层深入，众所周知，培养学生分析问题、解决问题的能力尤为重要，而能力的提高必须依靠重要的方式方法来达成，数学题“源于课本，高于课本”，“题海战术”的教学方式很难将学生的思维能力提升到更高的层次，故试卷讲评课中要善于以典型题目为原型，广泛寻求多种解法或导出同类的题型，把它们集中在一起，对其题目的立意、关键词、解题思路、解题策略和易产生的误区等点评、归纳和总结，让学生知其然，更知其所以然，培养他们的应变能力和发散思维，增强他们面对新问题敢于联想、分析和创新的意识，最终使每位学生都能感受到学习数学的乐趣和成就感。