数学学习的好助手——几何直观

安徽省合肥市马岗实验小学 李 婧

一、妙用几何直观，弄清题意

小学生的数学问题多以文字形式呈现，常常容易读不懂题意。根据其年龄特点，让学生自己在纸上涂一涂、画一画，借助线段图或实物图把抽象的数学问题具体化，还原问题的本来面目。画图策略是通过各种图形帮助学生把抽象问题具体化、直观化，从而使学生能从图中理解题意和分析数量关系，搜寻到解决问题的突破口。

图1

苏教版三年级上册有这样一道思考题（如图1）。这道题的数量关系比较复杂抽象，从字面上不易理解，容易混淆，而用图形表示它们的数量关系则一目了然。所以教学时，可以引导学生画出以下线段图（如图2）：

图2

有了这个线段图的支撑，学生很容易就能看出小芳比妈妈小的岁数就是小芳年龄的三倍，就可以用算式27÷3=9（岁）算出小芳的年龄，然后再根据已知条件算出妈妈的年龄。在这里，虽然有的学生画的图还很稚嫩，但是这种“数形结合”的策略，将有利于学生找准难点，化复杂为简单，化抽象为具体，化生疏为熟悉，从而理清题目中的数量关系，顺利解决问题。

二、妙用几何直观，理解算理

在小学数学的计算教学中，教师不仅要让学生明确算理，还要指导学生掌握算法，让学生体会数学计算从直观到抽象的变化，从而更好地对算理有深刻的认识和理解。算理是算法的理论依据，算法是算理的提炼和概括，它们是相辅相成的。从心理学角度来说，小学阶段学生的思维正处于由具体形象思维为主向抽象逻辑思维为主的过度阶段，所以在加、减、乘、除四则运算教学时教师不妨将几何直观落实到位，发挥几何直观对理解算理的作用。

三、妙用几何直观，化解难点

数形结合，其实质是将抽象的数学语言与直观的图形联系起来，使抽象思维和形象思维结合起来，通过对图形的处理，发挥直观对抽象的支柱作用，揭示数和形之间的内在联系，实现抽象概念和具体形象、表象之间的转化，发展学生的思维。

在教学单位换算时，我发现通过反反复复的练习，学生在课堂上能总结出单位换算的规律，但是在实际运用中，还是会出现这样那样的错误，究其原因，学生对单位换算的规律掌握不够牢固。在有一次的个别辅导中，受到学生想法的启发，我用数形结合的方式帮助学生深刻理解并记忆了大单位变小单位乘进率，小单位变大单位要除以进率的方法。

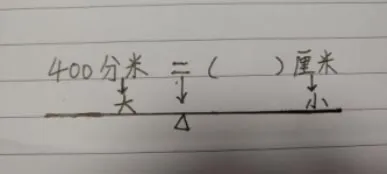
图3

比如，400分米=（ ）厘米，“=”就相当于天平的中心（见图3），两边的单位和数字就相当于天平两边的砝码，先让学生比较两个单位的大小，左边分米的单位大，右边厘米的单位小，为了使两边能保持平衡，那么左边的数字400就要小，右边需要填写的数字就要大。换算400分米=（ ）厘米时，要乘进率，等于4000厘米（见图4）。

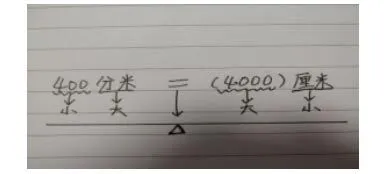
图4

利用天平的平衡原理进行解释，学生们轻而易举就掌握了单位换算的方法和窍门，做题时准确率也大大提高了。

四、妙用几何直观，探索概念。

许多数学知识的形成不一定依赖于论证和推理，通过直观地感知便能揭示出来。

例如，乘法分配律的教学历来是老师们关注的焦点，因为乘法分配律上课讲起来简单，但是一旦让学生进行简算就会出错。学生缺少亲身经历，对乘法分配律印象不深，做题时单凭死记硬背。我们不妨尝试新的学习方式，让学生借助直观图形参与到实验中，通过归纳推理、概括总结，得出结论，用起来才得心应手。

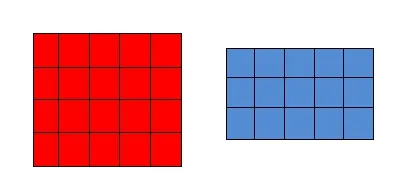
图5

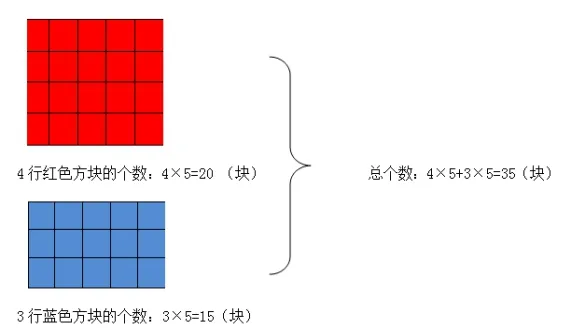
图6

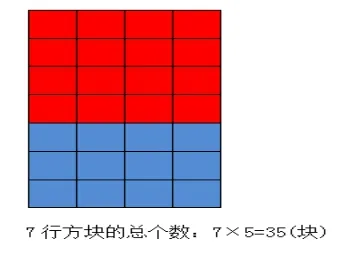
图7

教学《乘法分配律》时出示上图（如图5），让学生列综合算式计算图中方块的总个数。学生思考后得到两个算式“3×5+4×5”和“（3+4）×5”。让学生说说这两种方法先求什么，再求什么？根据学生的回答出示后面的图6和图7。教师相机总结，虽然算式的形式不同但是表示的意思相同，都表示7个5块。左右相等就可以用等号把两个算式连起来，那么也就是3×5+4×5=（3+4）×5。通过几何直观，唤醒了学生的生活经验，学生的两种算法让他们发现了算式间的关系，得到了乘法分配律研究的雏形，让学生理解规律的模型。

借助几何直观可以把复杂的数学问题变得简明、形象、促进数学的理解；通过图形进行观察，有利于信息回忆和方法的促成；根据直观认识来研究图形的性质和相关问题有助于数学问题结构的揭示。可以说，几何直观不仅解决“图形与几何”的学习中存在的问题，并且贯穿在整个数学学习过程中。因此，教师在教学中要准确地把握和深入地挖掘教材，适时运用几何直观，学生的核心素养就会得到进一步的发展，课堂的教学效率也能得以提高。