电力系统不良数据的检测与辨识算法研究

周嘉伦 刘可一 刘晓伟

摘要：以电力系统状态估计为背景，运用模糊聚类方法构建基于IEEE33含光伏系统仿真计算模型，采用模糊等价矩阵的聚类分析方法编写相关程序，对照仿真结果与理论结果，总结模糊聚类法对不良数据的辨识能力，为电力系统稳定运行提供参考。

关键词：状态估计;不良数据辨识;模糊聚类法;模糊等价矩阵

中图分类号：TM711    文献标识码：A    文章编号：1674-1161（2018）05-0013-04

近年来，电力系统的结构趋于复杂，普通的自动控制装置已无法满足要求，需构建联通系统设备和数据的总调度机构，集中进行监控、分析和决策，以及处理事故。电力系统存在大量变化的数据，其质量决定电力系统的稳定性。不良数据的产生原因主要有不合理布局、通讯传输不畅、人为误操作不当等。不良数据的检测与辨识是状态估计的重要内容之一，修正不良数据对于电力系统稳定运行具有重要意义。

1 电力系统不良数据的检测与辨识算法

1.1 残差方程

要获取残差值，需在完成每一次电力系统状态估计后，借助量测方程获得的新数据，与迭代的上一次数据作差。残差值处理可辨识电力系统中的不良数据。

如果系统状态可以检测，由式（1）可发现向量Z和X的关系，但数据没有被完全利用。然而，Z会提供一个冗余信息K（K=m-n）作为局部测量误差，K被称为“测量冗余”。任意一个本地测量错误K或者不良数据可能不会被检测或辨识。通过式（4）估计多个不良数据。

1.2 模糊等价矩阵聚类分析

1.2.1 量测数据标准化获取 对U进行量测，构建特征指标矩阵，并采用数据标准化方法（欧式距离法）对U*进行处理。特征指标矩阵U*的第j列：

即能得到标准残差RN和量测差值ΔZ的平均值和标准差，然后进行变换：

能够使规格化矩阵U0服从标准正态分布。

1.2.2 构建模糊相似矩阵 分析ui和uj的相似度，可用最大最小法：

得到相似系数rij，构成模糊关系矩阵R=（rij）n*n。

1.2.3 构建模糊等价矩阵 矩阵R只具有自反性和对称性，还需满足传递性，可引用传递闭包法得到传递闭包t（R）。

RE=R2ks=Rks·Rks=Rks=t（R）             （10）

在[0，1]范围内适当选取阈值λ，求出t（R）的λ截矩阵t（R）λ，并依据如下原则对其聚类，设t（R）λ=（rij）n*n，则：

rij（λ）=1 rij≥λ0 rij<λ               （11）

λ的范围在0～1中从1按步长逐次递减，可以得到不同的系统动态聚类的结果。

理想状态中，对可疑数据的辨识结果为部分良数据，其余部分为不良数据，那么聚类数为2。但实践证明，如果多个不良数据互相作用产生偏差，辨识的准确度大大下降。

根据上述状况，选择最佳阈值λ是聚类分析的关键环节。阈值越大，辨识精度越高，聚类个数越多，误判的可能性越大;阈值越小，辨识精度越低，聚类个数越少，漏检的概率越大。所以要同时考虑辨识精确度和判别的正确度，协调分类阈值λ和聚类数k的变化率。

式中：i为λ从小到大的聚类次数;ki和ki+1分别为第i次和第i+1次聚类数;λi和λi+1分别为第i次和第i+1次聚类时的阈值。

如果：

λ=max（λi）Ci=min（Cj）                   （13）

则认为第i次聚类的阈值λ为最佳阈值。

通过式（13）协调辨识精确度和系统判别准确度的关系，得到较好的聚类分析结果，使其成为最佳聚类结果。

2 基于IEEE33含光伏系统的仿真计算参数

运用MATLAB仿真模拟33节点的电力系统，假设其能实时获取电力系统真实的潮流数据。在算例分析中，先正向进行3个时间点的电力系统状态估计，利用标准残差法与模糊矩阵对测量进行动态分类，并确定最佳分类，分成良数据和不良数据两类，以便后续对不良数据进行修正。然后，人为设置不良数据，反向试验已知存在的不良数据能否被检测出来。当不良数据数量较多且互相影响较大时，会发生残差淹没和残差污染的现象，仅采用残差检测会导致正确性偏低，而标准残差法和模糊聚类相结合的方法，可以大大提高不良数据检测与辨识的可靠性。

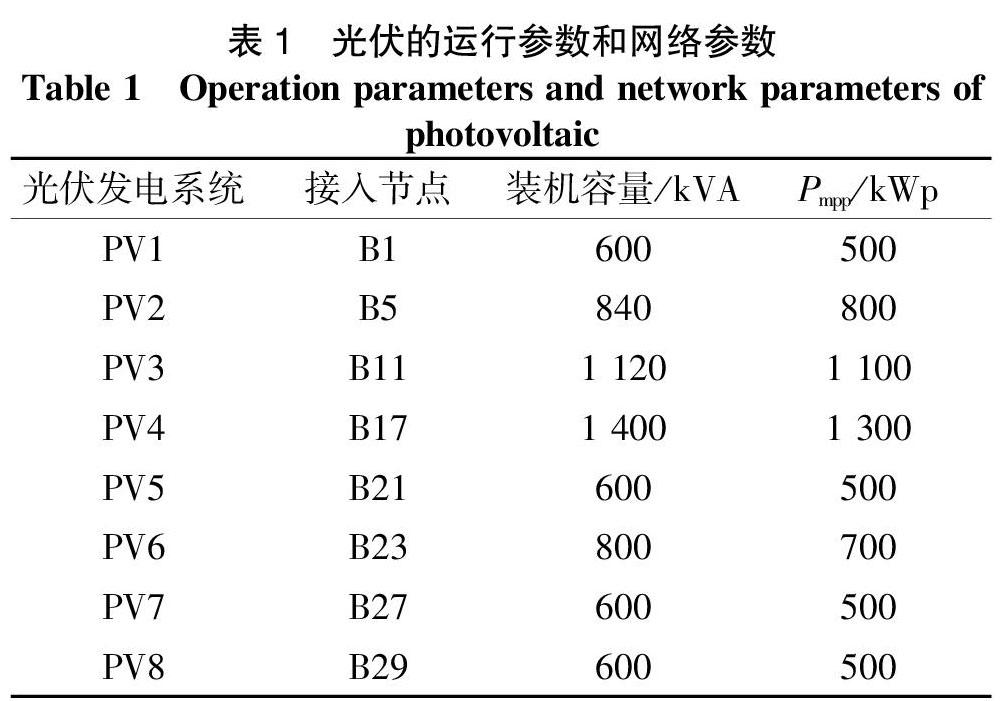
该网络中的负荷为恒功率PQ节点，整个系统的有功功率3 715 kW、无功功率2 300 kvar。在1，5，11，17，21，23，27，29节点分别添加光伏发电系统，光伏发电的运行参数及网络参数见表1，出力数据见表2。设置系统钟采集数据频率为每分钟。IEEE33节点的系统参数见表3，网络拓撲图如图1所示。

网中有32条支路、5条联络开关支路、1个电源网络，首端基准电压12.66 kV，三相功率准值取10 MVA，网络总负荷5 084.26+j2547.32 kVA。

3 不良数据的辨识与方法验证

3.1 不良数据的辨识

辨识不良数据时，取8，9，10时采集的数据，表示方法为：节点注入功率用Pi表示，支路有功功率用Pij表示，电压模值用Vi表示。选取8，9，10时刻的标准残差和残差协方差矩阵部分分类数（见表4和表5）。

首先，計算出在8时和9时，λ=0.85;在10时，λ=0.90。该系统可以得到最佳聚类的分区方式。假设在这种分区方式中，所有的量测量均为一类。而在结果中，8时在分区外出现了残差越限现象，原因可能是仿真运算过程中的近似计算导致的误差，可能发生残差污染;在9时和10时，系统存在不良数据，成功地被检测出来，没有出现残差淹没的现象。用虚拟量代替系统中的不良数据后，再一次进行状态估计计算，直至满足要求。

3.2 不良数据的辨识方法验证

为进一步验证标准残差检测对不良数据的检测和辨识效果，讨论系统在8时是否会存在残差污染和残差淹没现象，人为地加入一些不良数据。

在P9-10添加50%的不良数据，残差法和模糊聚类法均监测到测点42的不良数据。当系统存在单一不良数据时，根据检测结果可知，标准残差检测法和状态估计法能有效辨识出不良数据。

在Q9-10添加-50%的不良数据，在Q30添加+25%的不良数据，残差法和模糊聚类法均监测到测点30和42的不良数据。当系统存在少量不良数据且相互影响较小时，标准残差检测法和状态估计法均能有效辨识。

在P9-10添加50%的不良数据，在Q9-10添加-50%的不良数据，在Q30添加+25%的不良数据，残差法仅能检测到测点42，模糊聚类能检测到测点30和42。当系统中存在3个不良数据，且有可能互相影响且影响较大时，仅通过残差检测无法检测出测点30的不良数据，需进行下一步状态估计。由于有功和无功量测量均在测点42，所以模糊聚类辨识结果中只显示2个不同测点的结果，结果相同的测点未完全显示。

由上述验证可知，当系统中存在的不良数据数量较少且相互影响较小时，利用标准残差方法检测与辨识不良数据的效果较好;而当系统中出现的不良数据数量较多或者相互之间影响较大时，仅通过标准残差方法可能会出现残差淹没现象，导致部分不良数据不能被辨识。遇到此种情况时，要结合模糊矩阵的聚类方法。在较为复杂的系统中，相比其他不良数据辨识方法，利用该聚类方法可有效避免残差污染和残差淹没，为不良数据的修正奠定良好基础。

参考文献

[1] 周小宝.电力系统状态估计不良数据检测与辨识方法研究与应用[D].长沙：湖南大学，2013.

[2] 陈波.电力系统不良数据辨识的研究[D].广州：华南理工大学，2010.

[3] 刘辉舟，周开乐，胡小建.基于模糊负荷聚类的不良负荷数据辨识与修正[J].中国电力，2013（10）：29-34.

Study on Detection and Identification Algorithms of Power System Bad Data

——Based on IEEE33 including Photovoltaic System Simulation Calculation

ZHOU Jialun1，2， LIU Keyi1，3， LIU Xiaowei4

（1. College of Information and Electrical Engineering， Shenyang Agricultural University， Shenyang 110161， China; 2. State Grid Shenyang Electric Power Supply Company， Shenyang 110000， China; 3. Measurement Center， State Grid Liaoning Electric Power Supply Company， Shenyang 110000， China; 4. Dalian Rural Power Supply Service Co.， Ltd.， Dalian Liaoning 116001， China）

Abstract： Against the background of power system state estimation， the fuzzy clustering method based on IEEE33 including photovoltaic system simulation model was constructed. The fuzzy equivalent matrix clustering analysis method is used to write the related program to contrast the simulation results and theoretical results， summarizes the fuzzy clustering method for bad data identification ability， in order toprovide reference for stable operation of power system.

Key words： state estimation; bad data identification; fuzzy clustering method; fuzzy equivalent matrix