基于FFT和聚类分析的信号特征降噪算法

罗仕乐，郭星东

（韶关学院 数学与统计学院，广东韶关512005）

Fourier变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用［1-4］.数字信号处理是Fourier变换众多应用中比较重要的一类，运用Fourier变换，可以得到周期性数字信号的时域和频域，从而提取信号特征［5］.快速Fourier变换(Fast Fourier Transform，简称FFT)是20世纪的十大算法之一，FFT运用二分技术改进了Fourier变换在计算机上实现的效率，已成为目前流行的Fourier变换快速算法［6-7］.

由于实际应用中的数字信号往往含有噪声，运用FFT对数字信号进行处理的结果会有一定程度的误差，影响计算结果的有效性.为了尽可能减小误差的影响，本文结合FFT和聚类分析方法建立信号特征降噪算法，并通过数值试验展示算法的有效性.

在后续讨论中，用i表示虚数单位.

1 算法建立

考虑正弦波的叠加情形：

其中：t为时间变量，Ak,hk(k=1,2,…,N)分别表示第k个信号的振幅和频率，带有随机噪声的函数¯f(t)=f(t)+ε其中ε为随机噪声.

数字信号通过Fourier变换，可以转换到频域上进行研究.函数f(t)在N个点{}上的最小二乘离散Fourier变换为：

为了避免受到Fourier变换结果误差的影响，对Fourier变换结果进行聚类分析［8］，期待通过聚类过程能把由随机噪声造成的无关频率过滤，从而留下真实的频率信息.聚类分析是经典的多元统计分析方法，其应用的难点在于聚类数的确定.计算Fourier系数的误差可得：

式（1）表明，Fourier变换所得到的频域向量的误差与初始噪声ε是线性关系.这意味着利用初始随机噪声的方差上界来给出聚类数量的上界，会是一个较好的准则.综合以上讨论，给出信号特征降噪算法如下：

第1步：对信号函数进行FFT，得到频域分布向量和振幅向量；

第2步：对频域分布向量进行聚类，根据聚类结果去除噪声，得到更新的频域分布向量；

第3步：利用振幅和频域分布向量还原得到原数字信号.

注 算法第2步的聚类过程，可采用经典的K-Means聚类方法，根据式(1)，参数K的选择可结合输入信号的噪声方差水平来设定，可见数值试验的细节.

2 数值试验

通过MATLAB数值试验展示数字信号降噪算法的有效性.

考虑由两个正弦波叠加得到的如下数字信号：

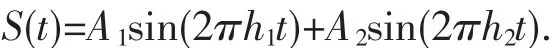
给上述信号加上随机噪声：

其中ε表示服从一维标准正态分布的随机变量，κ是给定的参数，用于控制误差的变化幅度.从t=0开始，以0.001为间隔，取50个时间节点用于FFT的计算.

在后续试验中，取A1=0.8,A2=1,h1=80,h2=120，ε使用MATLAB的randn函数随机生成，借助MATLAB的聚类函数clusterdata，聚类算法链接生成的层次树中保持的最大簇数设置为3，分别令κ=1,2,3,4,5,6，上节算法的运行结果分别如图1、图2和表1所示.

图1 信号恢复对比图(κ=1,2,3)

图2 信号恢复对比图(κ=4,5,6)

表1 不同情形下聚类降噪后所得频率结果

由计算结果可见，当κ=1,2,3,4时，经过聚类降噪处理后，FFT结果信号恢复的效果较好，振幅和频率都跟真实值吻合；而当κ=5,6时，信号恢复效果较差，第二个正弦波的频率估计结果都出现了误差.

由于该信号的噪声方差为κ2，当κ=5,6时，该信号的方差已远远超过了该信号函数的最大理论振幅值2≈2.56，因此，频率的估计出现误差是正常的.注意到，在κ=3,4时，本文的算法仍然得到了很好的信号还原效果，这表明了引入聚类分析所建立算法的有效性.

3 结语

本文利用FFT和聚类分析构建了信号特征降噪算法，结合高效的FFT方法，聚类方法的引入可以过滤原数字信号的噪声，数值试验展示了新算法的有效性.本文的分析方法和数值试验思路可以推广到其他类型的数字信号应用中.