基于模拟退火算法的FPSO系泊系统数值计算与仿真

2018-02-15纪柯柯姬艳伟盛进路

实验科学与技术 2018年6期

纪柯柯，姬艳伟，叶鑫，盛进路

(1.重庆交通大学交通运输学院，重庆南岸区 400074；2.重庆交通大学国际学院，重庆南岸区 400074)

E-mail:forwardlulu@163.com

随着海洋资源的开发和浮游平台作业的需要，系泊系统设计的重要性越来越引起人们的关注。FPSO作为一种浮标生产储卸油平台，被广泛使用于近浅海油田中。在近浅海水域，由于水浅，为防止锚的提升力，需要较长的系泊链，系泊系统将覆盖较大的海域，增加海域使用费[1]。根据海域的实际状况，设计完成海域作用范围小，设备精确度高的系泊系统，就显得尤为重要[2]。

锚泊系统优化受多种变量的影响，包括锚链型号、锚链倾斜角以及浮标的吃水深度等，国内外学者对系泊系统优化问题有着不同方法。采用神经网络和遗传算法对系泊线长度参数进行优化，有效地证明了该优化算法的可行性[3]，但只达到局部收敛，难以实现全局最优；神经网络算法可以对锚链方位角和锚链距离进行优化设计[4]，但变量参数不容易考虑全面；只对某单一成分的锚链长度和浮角优化，采用遗传算法优化结果较为准确[5]，但处理时间较长；针对深水多成分条件下，多目标锚泊系统优化模型，考虑因素较为全面，对问题的解决较为有效[6]，但忽略了FPSO的动力响应效应。

本文利用模拟退火算法的全局最优功能，分别以使浮标吃水深度最小、浮标平台的游动区域最小和钢桶倾角最小为目标函数，以浮标的吃水深度和钢桶倾斜角度为约束条件，对不同目标函数下的系泊系统进行分析仿真，再通过模拟退火算法的全局最优功能，求解出系泊系统的运行状态值。

1 基于模拟退火算法的优化模型构建

1.1模拟退火算法思想

模拟退火算法即是通过对当前解重复进行“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步缩减控制参数的值，退火终止时的解即为系统最优解。该方法可在局部最优解情况下，概率性地跳出并最终趋于全局最优。目前很多人选择遗传算法求解组合优化问题，但会出现收敛于局部最优的现象，而达不到全局最优，会导致计算时间加长，复杂程度加大[7]。

1.2模型的建立

实际的锚泊系统中，锚泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成，如图1所示。系泊系统的优化设计就是使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。

图1 传输节点示意图

本文算法的主要思想是在未知不可预见的环境下，假设锚链由若干相同链环连接而成，且不考虑各连接点之间的摩擦力作用，仅受水流力和风速的影响，采用静态分析方法计算锚链惯性力和拖拽力[8]，求解出不同锚链型号在该环境下的钢桶倾角、游动半径和吃水深度的计算数值[9]，以便选择合适的系泊系统作业，以使浮标吃水深度最小、浮标平台的游动区域最小和钢桶倾角最小为目标函数，以浮标的吃水深度和钢桶倾斜角度为约束限制条件。根据上述假设和分析，目标方程可表述为：

min(k1h,k2R,k3θ)

(1)

约束条件为：

式中,h、R、θ分别为吃水深度、浮动半径以及钢桶倾角；k1、k2、k3仅为优化系数，无具体含义。

锚链静平衡方程为：

(2)

(3)

式中，T为锚链拉力，Fx为单位长度上切向流拽力，Fy为单位长度上的法向流拽力，w为锚链单位长度的质量，ε为锚链单位长度的延伸。

钢桶倾角方程为：

(4)

式中，F=Fw+Fh，

G=Ga-4G1-Gf-G2/2

式中，θi为钢桶倾角，G为所求目标以下物体的总质量，Ga为系统的总质量，G1为钢管的质量，Gf为浮标的质量，G2为目标质量，Fw为近海水流，Sw为物体在水流速度法平面的投影面积，Vh为水流速度，Fh为近海风载荷，Sh为在风向平面的投影面积，Vh为风速，l为每节链环长度。

浮标浮动范围方程为：

(5)

浮标吃水深度方程为：

(6)

先对整个系统进行受力分析，通过相互之间的平衡关系，建立方程[10]；然后分别以每根钢管、每根锚链为单位，考虑系泊系统所处的外部环境，以及波浪力、风力等的影响，对其进行静力分析；分别以浮标吃水、游动半径、钢管倾角最小为目标函数，建立求解方程；并运用MATLAB软件编程，在模拟退火算法全局优化的状态下，计算得出钢管倾角、浮标吃水深度和游动半径[11]。在给定的锚链型号参数范围内，选择最优系泊系统，以便在不同环境下适用。

2 系泊系统模型设计

2.1 锚链参数

将浮标系统视为底面直径2m，高2m的圆柱体，浮标质量为1000kg。锚质量为600kg,锚链采用无挡普通链环，近浅海锚链型号和参数如表1所示。钢管共4节，每节长度1m，直径为50mm，每节重量为10kg。

表1 锚链型号和参数表

2.2 环境参数

在近浅海环境下，由于潮汐等因素的影响，风、浪、流等环境因素的作用方向同向，布防海域深度为16～20m，海水表面流速为1.5m/s、风速为36m/s。

2.3 计算算法

算法包括以下6个步骤[12]。

1)初始化操作。令当前温度T=T0，即开始退火的初始温度，此时初始解状态为S0，并计算相应的目标函数值E(T0)。

2)令T等于冷却进度表的下一个值Ti。

3)根据当前解Si进行扰动，产生一个新解Sj，计算相应的目标函数值E(Sj)，得到ΔE=E(Si)-E(Sj)。

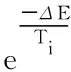
5)在温度Ti下，重复N次扰动和接受过程(N为Markov链的长度)，即执行步骤3)和步骤4)。

6)判断温度T是否等于Ti，是则终止算法；否则转到步骤2)继续执行。

3 计算结果与仿真

以最小浮动范围为目标函数的系泊方案布置如表2所示。表2中，计算求解得到在5种不同锚链型号下的倾斜角度、浮动区域半径和吃水深度等若干因素下的结果。由于限制浮标的吃水最大为2m，因此型号Ⅲ、Ⅳ、Ⅴ都不符合限制要求。在符合限制条件的情况下，锚链Ⅰ的游动范围最大在26m左右，可达海水深度为8～9m，中间设有配重球；此时锚链Ⅱ的游动范围在32m，可达海水深度为14～15m。型号Ⅰ的浮动区域半径相对最小，但锚链Ⅱ可到海底深度优于锚链Ⅰ。因此，在近浅海深度小于8m时选用锚链Ⅰ较优，深度在8～14m内选用锚链Ⅱ较优。

以最小钢桶倾角模型求解的结果如表3所示。由表3可知，锚链Ⅰ和锚链Ⅱ吃水深度均在2m以下，且两者的浮动区域半径不大，但锚链Ⅱ的可达深度大于锚链Ⅰ，因此，锚链Ⅱ具有较好的适用性。

以最小吃水深度为模型求解的结果如表4所示，5种型号的锚链均满足限制要求。锚链Ⅰ浮动区域半径在25m左右，且吃水深度最小。因此，当海水深度在9m内时，锚链Ⅰ较优。

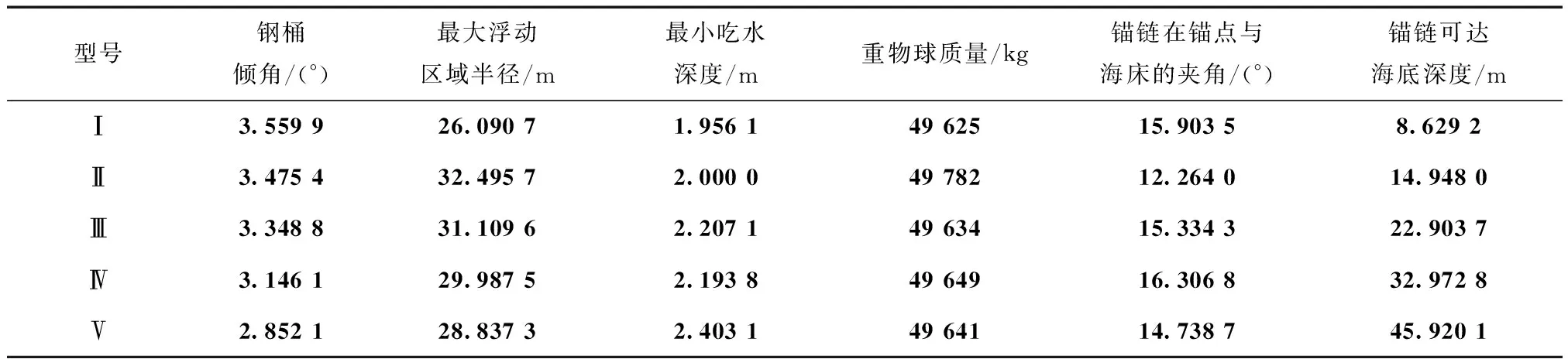
表2 最小浮动范围下模型各指标状态数据

表3 最小钢桶倾角下模型状态各指标数据

表4 最小吃水深度下模型状态各指标数据

为了验证计算结果的可靠性和推广实用性，分别以最小浮标游动半径、最小钢桶倾角和最小吃水深度为目标建立求解方程。基于MATLAB仿真模拟，在最小浮标移动半径目标条件下，仿真图如图2所示，每种状态下锚链可达海水深度以及浮标浮动区域均不相同，其中转折点以下部分为锚链游动状态仿真图。

图2 最小浮动范围下仿真图

由以上仿真结果分析可知在近浅海区域内，采用每节锚链长度较短、单位质量长度较轻的锚链型号，有利于提高整体系泊系统工作效果，并且节约经济成本。由不同模型数据对比可得，随着锚链长度和质量的不断增加，锚链摆动幅度逐渐增大，与纵断面的夹角也逐渐增大，但钢桶倾角的变化不大，对系泊系统的实际工作无较大影响。通过以上分析，可知为了提高系泊系统的工作状况，可以将浮标制作成流线型，以减小其受到的水流力冲击，并根据系泊系统布置位置的不同，合理选择锚链型号。