基于遗传算法的PC构件工厂排产研究

(1.中建三局绿色产业投资有限公司，武汉 430074；2.湖北工业大学计算机学院，武汉 430068； 3.湖北工业大学土木建筑与环境学院，武汉 430068)

引言

随着装配式建筑项目的持续深入推进，近几年建筑产业化基地在全国各地相继落成，PC构件工厂纷纷拔地而起。由于装配式建筑项目的规模和数量不断增加，客观上要求PC构件工厂生产效率不断提高，生产产能持续增长。排产是生产中的一种匹配方式，不同的排产模式对应不同的匹配方案，目的使生产产能最大化和各生产线负载实现均衡[1]。一方面，由于建筑工程体量大、建筑结构复杂，构件具有数量众多、类型复杂的特点，造成构件设计标准化程度低，不利于构件的批量生产；另一方面，构件工厂的数字化管理水平不高，还处于手工或半自动化生产方式，生产自动化程度低。以上两个因素造成现有PC构件工厂排产调度系统性差，未达预期设计生产能力。研究构件排产调度方案，提高构件生产产能，降低生产成本，具有重大的应用价值和现实意义。

由于排产调度是一个典型的NP问题，国内外在寻求最优解方面取得了一定成果。如武韶敏等提出一种面向订单多目标排产问题的改进遗传算法[2]。一些文献通过引入启发规则，研究多任务组成订单的排产模式[3-4]。目前，装配式建筑项目尚处于起步阶段，PC构件排产调度方案依靠人工制定，其准确性和客观性较差。目前国内学者对PC构件生产线排产有一定研究成果，但对于工厂级排产研究尚不多见[1]。

本文在对PC构件厂排产问题进行分析和数学建模，结合遗传算法提出工厂级的排产方法。实验表明，本文提出的方法能够提高多条生产线的生产效率，实现产能最大化。

1 问题分析和数学建模

通常，PC构件工厂车间布局多条混凝土预制构件自动化流水线，按流水生产线模块分为外墙生产线、内墙生产线、固定模台生产线和其他生产线，形成多构件多线体生产模式。预制构件排产是一个多流水线、多工序的离散的复杂生产过程[5]。由于外墙生产线能够生产内墙生产线的产品，且固定模台生产线用来生产复杂异型构件，本文研究对象是多条外墙生产线下工厂产能最优排产算法。外墙生产流水线上的工位包括清扫、喷涂、钢筋模板装配、预埋件安装、浇筑振捣、上层板放置、挤塑板安装、拉结件安装、网片安装、二次浇筑、振动赶平、预养护、抹面、养护、拆模、翻板吊运。适合生产的主要预制构件有内墙板、叠合板、隔墙梁、外墙板(单)、外墙三明治板。排产调度受PC构件类型规格、生产线数量、工序时间及次序关系等因素的影响。

问题分析 假设某个PC构件工厂配置L条外墙生产线，每一条生产线K个工序。现有类型M，数量N个构件构成生产任务单，不同类型构件的工序作业不同，求出生产任务单最优的排产方案，保证产能最大。

根据现场生产情况，本文对工厂排产过程进行建模，其约束条件如下：

(1)模台沿设定轨道顺工序向前移动，在该固定的工位上完成相应的作业；模台空间和时间约束关系具有传递性。

(2)每一条外墙生产线按照固定节拍排产模式进行生产。

(3)多条外墙生产线相互独立、工位配置一致。

(4)人工、物料、机械设备能够满足各工位的作业要求，所有生产能够按时完成。

N为构件数量，L为生产流水线总数，i为构件ID编号(i=1,2,…,n)；j为生产线编号(j=1,2,…,l)；Ri为每一个构件的类型，表示编号为i的构件工序数量；由于采用固定节拍，Ti表示类型为Mi构件的作业时间。Ki是一个长度K的序列，表示构件在生产线上的加工序列。

Pml是一个二维矩阵，表示编号为Mi构件需要在对应编号Lj生产线上加工，即构件生产线加工路线；Tml是一个二维矩阵，表示编号为Mi的构件在Pml对应的生产线上所需的加工时间。通过多条生产线负载均衡，让后续构件进入当前生产效率较高的生产线，对应最快完工时间的那个排产顺次就是排产结果。即

Tmin=min(∑Tml)

(1)

2 改进的遗传算法

本文结合生产情况和问题分析，提出基于改进的遗传算法的工厂级构件调度算法。遗传算法是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法，属于自适应寻优算法。

2.1 个体编码

采用一个 N×K的矩阵来表示遗传算法中的个体， 即一种生产任务单排产的解决方案，矩阵采用实数编码如下所示:

矩阵 A 的每一行代表一个构件，共有N个构件；矩阵每列对应的生产线的加工工序，也就是一个构件生产流程。 矩阵中元素的行标i表示第i个构件，列标j表示第j个工序。由于本文每道工序采用固定节拍时间，因此aij的取值是[T,nT]的整数，表示构件i的第j个工序进行加工，T为一个流水节拍作业时间。

2.2 初始种群的产生

初始种群的个体是按行产生的。为了满足构件生产约束条件，每个构件作业任务从第一道工艺流程开始随机产生加工时间at1∈[T,nT]，接着为第二道工艺流程分配加工时间at2∈[T,nT]， 以此类推完成单个构件的所有工艺流程的排产，进而完成所有构件的排产。

2.3 交叉算子

在遗传算法中交叉具有重要作用，当交叉概率偏大时，增强了遗传算法对新空间的搜索能力，但优秀基因遭到破坏的可能性也变大，算法收敛速度和稳定性下降；当交叉概率偏小时，遗传算法的搜索会有滞后性。随机在父代中选择交叉点盲目性很大，算法性能会严重下降，因此本文不考虑父代基因随机交换。由于构件按固定节拍生产，构件类型决定了构件作业时间，按照构件的类型把父代基因划分为若干个小段，同时针对工序相同作业时间的构件划分到一个基因段，划分完成后在父代中按作业时间顺序选取相同基因段组成一个子代。父代基因段适应度越高，被选作子代基因段的可能性越大。本文具体实现方法为：在杂交过程中,对父代中两个个体对应位上的值相加后采用模运算求余,从而得到子代个体。

2.4 变异操作

传统遗传算法的任务调度易陷入局部最优解,在改进的遗传算法中引入起辅助作用的变异算子并对其进行改进,以期增加种群多样性,从而实现改进算法所得解达到全局最优。考虑该变异算子作为辅助算子应具有简单易行的特点,本算法将传统变异算子作以下简单优化,改进为一个均匀变异算子,即可满足要求。设k=(k1,k2,…,kn)为参加变异操作的父代个体。具体实现方法如下：①以均匀概率选取随机数xi∈[1,q],(i∈N,i∈[1,n]),i从1至n依次取值；②以xi替换ki；③返回步骤①直至i=n 结束。从而得到新个体x=(x1,x2,…,xn)为变异后的子代个体。

2.5 适应值函数

遗传算法的适应度函数用来判断群体中的个体的优劣程度，它根据所求问题的目标函数来进行评估。

构件排产问题是求解加工耗费总时间的最小值，这需要让适应度值最大化，所以适应度函数定义为：

(2)

其中，tij为第i个构件第j道流水线的作业时间；Ki是加工第i个构件所需的最大工序数；n是构件数。

2.5 终止条件

当迭代次数超过给定值后，算法停止运行，此时得到的最优解就是排产调度所需的相对最优排产方式。

3 改进的遗传算法具体流程

本文的排产算法将贪心算法和遗传算法相结合，利用遗传算法进行子代繁衍，适应度应用局部贪心算法选择，保证时间复杂度和空间复杂度尽可能小的情况下来获取一种尽可能接近于最优的排产算法。改进的遗传算法操作步骤：

1)输入构件的种类、加工工序数和对应工序的作业时间；

2)设定算法的群体规模和结束的循环代数，设定算法的初始交叉概率和变异概率。设定初始解集作为初始染色体；

3)计算当前染色体适应度值，把函数适应度值最大的个体设定为当前一代的最佳解；

4)检验是否满足算法收敛准则，若满足，则转步骤7)，否则进行步骤5)；

5)对染色体当前的交叉概率和变异概率进行动态的自适应调整，以调整后的交叉概率进行改进的交叉操作，以调整后的变异概率进行变异操作；

6)对染色体进行选择操作，把经过遗传操作的染色体作为当前染色体。转步骤3)；

7)得到最佳个体，输出结果。

该算法的流程图如图1所示。

图1 改进的遗传算法流程图

4 排产仿真与结果分析

4.1 生产流水线建模

AnyLogic仿真软件作为一种创建真实动态模型的可视化工具，具有较强的设计离散、系统动力学、多智能体和混合系统的建模和仿真能力[1]。大量实际应用表明，借助AnyLogic工具，便于分析和挖掘带有动态发展结构及组件间关联关系，适合创建对象的动态模型[6-7]。PC构件厂排产是一个典型的多工序生产、多运输平台的离散和连续相结合的复杂生产过程，其生产流程具有工序多、人工干扰大、原料不稳定、各工位作业时间波动大等复杂系统的特性，生产组织和运行难度较大。由于外墙生产线可以替代内墙生产线生产，本文以外墙生产作为仿真对象，其生产线各工位之间的内部逻辑如图2所示。

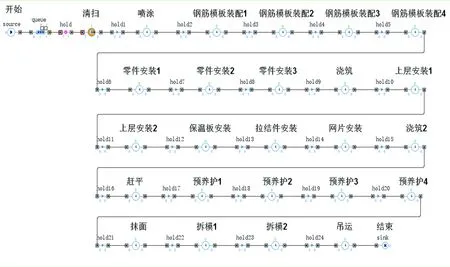
图2 外墙生产线内部工位关系

图3 外墙流水线生产流程模型图

建模约束条件包括：

1)外墙流水线包含16个工位，根据不同工位作业复杂程度，可扩展为25个子工位；

2)采用固定节拍排产模式；

3)养护窑工位的时间相对固定，按40个工位，每个15分钟计算；

本文使用Anylogic 7.0.2 professional创建PC构件外墙生产流水线模型，进行内部逻辑编程、运行仿真和数据统计等工作。按照上述工艺流程、生产逻辑搭建模型，模型图如图3所示。

4.2 实验数据

为了分析外墙流水线生产产能的影响，本文选取含窗构件、含门构件、含门窗构件和普通单墙等四种不同类型的PC预制外墙构件，每种类型构件数量均为75件。四种不同类型的PC预制外墙构件按工序不同可扩展为25个子工位。外墙流水线的数量为3条。由于不同类型构件的外观尺寸、体积、结构复杂程度等不一致，工序相同的构件作业时间不同，因此各个工序时间取决于构件类型。比如，外叶墙浇筑作业时间与构件类型有关，同时与构件形状、面积、体积有关；抹平时间与构件类型、面积有关；拆模时间与螺丝数量成一定比例关系；网片安装时间既取决于网片安装的面积，又受到出筋数量的影响等等。综合考虑上述多种因素，实验所用的4种不同类型外墙构件作业时间如表1所示。表1的数据全部来源于某构件工厂外墙流水线实际生产过程，是构件多批次多时段统计的结果。

表1 不同构件在各工位上的作业时间

4.3 仿真流程实现

本文基于某PC构件工厂进行建模，该工厂生产线有25个工位。按照图2所示构件实际的工艺流程，设计构件生产仿真过程，主要使用以下五种库模块，如表2所示：

表2 库模块及其功能

具体实施步骤如下：

(1) source模块生成Module构件类，并赋值该构件ID，同时创建时间集合；

(2) Module构件类进入queue队列模块排队，并从excel电子表格中获取各个工位的时间数据；

(3) Module产品类进入delay工位模块，锁上hold模块，防止其它产品在进来；

(4) 在deley工位模块加工该工位的时间，完成后将实际时间记录到timeList模块，之后离开该工位模块，进入下一个deley工位模块，同时解开hold锁模块，让下一个产品进来；

(5) Module构件类依次走完剩余deley工位模块，每次均记录工位的实际时间，开关hold锁模块；

(6) 完成所有deley工位模块的加工后，进入sink终点模块离开生产线，将每个工位记录总进行累加，求出总的时间；

(7) 后面构件同上述过程运行，最后输出所有构件的实际生产时间。

Anylogic仿真运行图，如图4所示。

4.4 实验结果分析

将标准遗传算法(SGA)[8]和本文算法应用于该PC构件工厂实际生产进行仿真对比。设定初始交叉概率0.70，变异概率0.05，种群规模M=300，进化代数T=100，分别独立运行20次取平均值。利用Anylogic仿真，得到的结果如表3所示。

表3 SGA和本文算法的排产结果

比较分析可得：本文算法波动率小，动态稳定性高，最优解为98.45，排产效果优于SGA。但由于引入贪心算法，本文算法运行时间比SGA明显缩短，运行时间减少比例为17.6%。

图4 外墙生产线仿真运行图

5 结语

结合PC构件工厂的生产实际，本文选用贪心算法和遗传算法各自优点，提出一种产能最大的排产优化方法，构建了排产优化的数学模型。引入贪心算法，设计了的改进遗传算法求解上述数学模型，提高了传统遗传算法的收敛速度。通过对算法对比，改进算法比SGA算法显著缩短了构件的加工时间，优化效果较为明显，对PC构件工厂产能提高有一定借鉴意义。