电能质量信号的KSVD NRAMP 归一化自适应稀疏重构算法

肖儿良 冯杰 简献忠 王如志

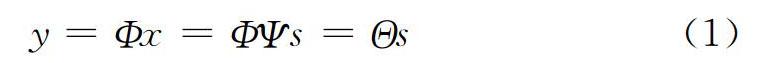
摘要：针对稀疏重构算法在电能质量重构中存在实时性差、重构精度低的问题，提出一种基于特征向量归一化的K奇异值分解（KSVD NRAMP）自适应稀疏重构算法。算法针对电能质量信号的非线性非稳态特征，采用迭代式匹配追踪得到信号稀疏特征矩阵，然后对矩阵进行归一化处理，量化特征向量，加快函数收敛速度。接着对得到的矩阵原子进行奇异值分解，改善迭代步长波动造成信号重构精度低的问题，最后构建信号的高斯随机矩阵并重构信号。当信号压缩率在50%～90%时，该算法重构信噪比其它重构算法的重构信噪比高出26dB～28dB。实验结果表明，该算法重构精度更高且计算时间短，为电能质量信号的研究提供了一种新思路。

关键词：归一化;奇异值分解;压缩感知;电能质量信号重构

KSVD NRAMP normalized adaptive sparse reconstruction

algorithm of power quality signals

XIAO Er liang1，2， FENG Jie1，2， JIAN Xian zhong1，2，WANG Ru zhi

（1.School of Optical Electrical & Computer Engineering， University of Shanghai for Science & Technology;

2.Shanghai Key Laboratory of Modern Optical System， Shanghai 200093， China;

3.College of Materials Science and Engineering， Beijing University of Technology，Beijing 100124，China）

Abstract：Due to the poor real time performance and low reconstruction accuracy of sparse reconstruction algorithm in power quality reconstruction， the author proposed an adaptive sparse reconstruction algorithm based on the normalized K singular value decomposition of eigenvector （KSVD NRAMP）. Firstly aiming at the nonlinear and unstable features of power quality signals， algorithm can obtain the sparse feature matrix of signals by adopting the iterative matching pursuit. Then the algorithm adopted the normalization processing of sparse feature matrix， quantizing eigenvector， accelerating the convergence speed of the function. Afterwards， aiming at the obtained matrix atoms， the algorithm can realize the decomposition of the singular value and improve the problem of low signal reconstruction accuracy caused by the fluctuation of iterative step. At last， the algorithm can construct the Gaussian random signals matrix and reconstruct the sparse signals. When the signal compression ratio is between 50% and 90%， the reconstruction SNR of the proposed reconstruction algorithm is 26dB ～ 28dB higher than that of other reconstruction algorithms. Experimental results show that the proposed algorithm has higher reconstruction accuracy and shorter computation time， and provides a new idea for the study of power quality signals.

Key Words：normalization; singular value decomposition; compressed sensing; power quality signals reconstruct

0 引言

電能质量信号监测[1 4]是配电网避免设备损坏、确定干扰原因的主要方法[5]，电能质量的好坏不仅关系到电网企业的产品质量，也影响到用户的安全运行。因此，对电能质量信号的检测分析具有非常重要的意义。

现有的处理方法主要包括基于短时傅里叶变换方法（STFT）[6]、小波变换（WT）[7]、希尔伯特–黄变换（HHT）[8]、S变换（ST）[9]等。但以上信号处理方法均建立在传统的奈奎斯特采样定理基础上，要求采样频率较高，导致电能质量信号分析复杂、功耗较大。为解决上述问题，学者们进行了很多研究[10 12]，如文献[12]将压缩感知理论应用于电能质量信号识别中，验证了该方法的可行性;文献[13 14]采用固定正交基稀疏分解方法，具有构造简单、实现快速、复杂度较低的特点。由于采用固定正交基进行信号分解，从而导致稀疏系数表达能力和范围有限，为解决该问题，文献[15]采用一组在过完备的离散余弦基上分解信号的方法，重构效果优于固定正交基。但由于稀疏字典生成时未充分考虑电能质量信号时频特性，且采用的基原子结构固定，不能实现信号的最优表示，由此导致稀疏字典不具有自适应性，不利于工程实际应用。因此，文献[16]提出KSVD ROMP算法，利用字典学习方式自适应地构造信号的变换基。但是该算法的稀疏特征矩阵原子差异巨大，迭代结束条件受步长波动影响较大，导致该算法应用于信号重构时存在实时性差和重构精度低的缺点。

针对该问题，本文提出一种KSVD NRAMP算法，即基于特征向量归一化的K奇异值分解自适应稀疏重构算法。首先根据电能质量信号非线性非稳态特征，采用迭代式匹配追踪得到信号的稀疏特征矩阵，然后对矩阵原子进行归一化处理，将特征量缩放，缩小特征矩阵原子差异，使其梯度下降过程更加笔直，加快函数收敛速度从而加快计算速度。接着利用训练学习的方式对得到的系数矩阵进行奇异值分解，然后从字典中选出一组和原始信号或残余最匹配的原子更新字典，以获得信号的最优展开函数，改善算法迭代结束条件受步长波动的影响。与DCT算法、KSVD ROMP算法相比较，结果显示本文算法计算时间最短，重构精度更高，可很好地用于电能质量信号重构中。

1 壓缩感知与过完备字典

压缩感知[17 19]的核 心思想为：若一个R N空间的信号x为长度N的一维信号，信号x稀疏度为k（即含k个非零值），或在某个正交基Ψ上具有稀疏性，那么可将原始信号x通过一个与正交基Ψ不相关的测量矩阵ΦMXN（M>K，M<<N）进行非自适应线性投影，得到保持原始信号结构且远小于信号长度的测量值y（M×1）。最后通过求解数值最优化问题精确重构原始信号x。一般的自然信号x本身并不是稀疏的，需要在某种稀疏基上进行稀疏表示：x=Ψs，Ψ为稀疏基矩阵，s为稀疏系数（s只有K个是非零值（K≤N））。将原来的测量矩阵Φ变换为Θ=ΦΨ（Θ 称之为传感矩阵），压缩感知观测模型如式（1）所示。

常用的稀疏基有快速傅里叶稀疏变换基（FFT）、离散小波变换稀疏基（DWT）、离散余弦变换稀疏基（DCT）等正交变换矩阵。由于电能质量扰动信号时频变化范围较广，在上述变换基 Ψ下仍会不稀疏或不够稀疏，因此可采用适合信号本身特征的过完备字典D对信号进行稀疏表示。式（2）所示为信号在过完备字典D域下的变换过程，稀疏系数s利用字典D变换为信号X，再经过观测矩阵Φ得到压缩感知观测值Φ为随机矩阵。过完备字典D为 非正交基，可以较好满足压缩感知的非相干性，即满足RIP性质[14]：

2 KSVD NRAMP算法

2.1 KSVD NRAMP算法

在信号的稀疏表示中，选择不同的冗余字典，信号重构效果不同。常用的冗余字典包括随机字典、DCT 字典、傅里叶基字典以及小波基字典[13 15]等。为有效训练一个用于信号稀疏表示的字典，Elad&Aharon[20]提出K奇异值分解算法，可同时更新当前原子和相应的稀疏系数。通过字典学习方式得到的过完备字典能自适应地对信号进行很好的稀疏表示。本文根据信号本身非线性非稳态特征训练学习过完备字典，这类字典中的原子与训练集中的信号本身相适应。与基于正交基方法字典相比， 通过学习获得的字典原子数量更多， 形态更丰富， 能自适应地与信号本身的结构匹配， 具有更稀疏的表示。

令 n维矩阵D∈Rn×K为学习训练后的过完备字典，y∈R n及x∈R n分别代表训练样本信号和对应的稀疏表示向量，矩阵Y={y i} N i=1为N个训练信号样本组成的集合，矩阵X={x i} N i=1 表示每个信号样本所对应的稀疏解向量所组成的集合，T 0 为各稀疏表示向量中非零元素总数的上限，则KSVD NRAMP算法的学习目标可以表示为：

因为电能质量信号为一维信号，所以将信号数据 S以长度N分割得到原子，之后随机选取k个原子组成样本集合x 。

KVSD NRAMP算法关键步骤：①稀疏编码阶段。在该阶段， 根据电能质量信号的非线性非稳态特征，采用迭代式匹配追踪得到信号的稀疏特征矩阵，然后对矩阵原子进行归一化处理，将特征量缩放至[0，1]区间，缩小特征矩阵原子差异，使其梯度下降过程更加笔直从而缩小特征矩阵原子差异，加快函数收敛速度以加快计算速度，得到归一化处理后的初始稀疏系数矩阵 X;②根据训练迭代误差，利用训练学习方式，对得到的初始稀疏系数矩阵X进行奇异值分解，然后从字典中选出一组和原始信号或残余最匹配的原子更新字典，以获得信号的最优展开函数，改善算法迭代结束条件受步长波动造成的信号重构精度低的问题。将回溯思想和逐步搜索原子字典更新相结合，添加段变换和步长信息，在反复迭代过程中不断调整步长，进行残差r比较，动态探测并且逼近信号x的实际稀疏度。在每一次迭代中，S（索引集）利用式（5）获得测量矩阵Φ 的各个测量值：

本轮迭代的候选集合 C是由本轮索引集S与上一轮迭代中的稀疏系数矩阵F合并而来，而当前迭代的稀疏系数矩阵F是仅当上一轮迭代中计算出的新残差值小于原来残差值时，由当时迭代的候选集合C 赋值而来。

本文根据电能质量信号非线性非平稳特征，构建一个MXN的高斯随机矩阵作为观测矩阵，设计方法为：构造一个大小为MXN的矩阵 Φ，使Φ中的每一个元素独立服从均值为0、方差为1/M的高斯分布，如式（4） 所示。

该观测矩阵具有很强的随机性。实验证明，用本文观测矩阵观测电能质量信号样本时，其不仅满足约束等距条件，且几乎与任意稀疏信号都不相关，所需测量次数最少。通过实验分析，观测效果优于一致球测量矩阵、二值随机矩阵以及局部傅里叶矩阵。

2.2 算法流程

（1）使用MATLAB仿真得到9种电能质量扰动信号样本，将样本 随机分成S，X两部分，S部分为用于生成电能质量信号学习字典，X部分用于产生压缩感知框架 下的观测矩阵。

（2）通过 数据S得到电能质量信号初始学习字典以及待训练样本集合Q，再采用贪婪迭代匹配追踪得到初始稀疏系数矩阵F 。

（3）稀疏系数矩阵 F中的特征向量进行归一化处理，将特征量缩放至[0，1]区间，得到归一化处理后的矩阵F i 。

（4）用训练学习的思想对步骤（3）得到的矩阵原子进行奇异值分解，每次分解从字典中选出一组和原始信号或残余最匹配的原子更新字典，以获得信号的最优展开函数，并交替更新字典原子。

（5）将回溯思想和逐步搜索原子字典更新相结合，添加段变换和步长信息，在反复迭代过程中不断调整步长，比较残差 r，动态探測并且逼近信号x 的实际稀疏度。

（6）用公式（4）设计M×N维的高斯随机观测矩阵 Φ 。

（7）初始化残差 r 0=y，size=step，阶段stg=1 。

（8）若 r new/r y<sigma，则 不进入迭代，直接进入步骤（11），否则进入步骤（9）。

（9）利用式（6）计算出 u，取前最大的size个对应索引值构成索引集合S 。

（10）获得索引集合 C=S∪F，同样利用式（5）计算出F new ，利用式（7）得到新的残差。

（11）如果满足终止条件，则退出迭代，进入步骤（8），否则进入步骤（7）。

（12）如 ‖r new‖ 2≥‖r pre‖ 2，则stg=stg+1，size=stg×step，否则r pre=r new，F=F new ，进入步骤（2）。

（13）利用最小二乘法，求出最优稀疏系数 =（R TR）-1·R Ty 。

（14）得到 后，利用步骤（3）经归一化处理后的矩阵F i及步骤（5）中的观测矩阵Φ可得重构信号=ΦF i 。

3 实验

3.1 硬件环境及信号模型

为了验证本文算法的有效性及优越性，硬件环境统一采用Win7 32位操作系统，4GB内存，Intel Core i5-2410M CPU 2.30 GHz，利用Matlab 2010b生成9种电能质量信号（电压暂降、电压暂升、电压尖峰、电压缺口、电压振荡、电压谐波、电压中断、电压脉冲以及电压闪变）各1 500个样本，如图1所示，信号的采样频率为6 400Hz，电压基波频率为100Hz，信号长度N=600，测量次数M=128。

3.2 性能指标重构评估

为了客观评估分析本文KSVD NRAMP算法在电能质量信号稀疏重构应用中的性能，采用式（8）～式（11）中的均方误差百分值（MSE）、重构信噪比（SNR）、能量恢复系数（ERP）以及压缩率（CR）4项指标，对本文方法与DCT算法、KSVD ROMP算法进行重构效果评估，同时通过程序计算时间比较3种算法的实时性。

3.3 实验与分析

3.3.1 重构误差与计算时间对比

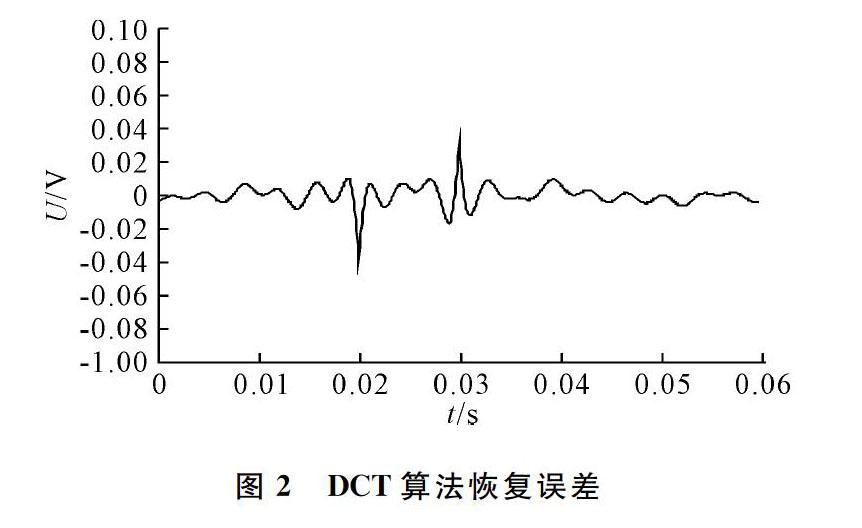
本次实验使用DCT、KSVD ROMP及KSVD NRAMP3种算法分别对电压骤降信号进行稀疏重构。图2为DCT算法恢复误差，图3为KSVD ROMP算法恢复误差，图4为KSVD NRAMP算法恢复误差。表1为3种算法对电压骤降信号稀疏重构200次的平均运行时间。由图2、图3可知，在扰动信号出现和结束时，DCT与KSVD ROMP两种算法由于生成的稀疏特征矩阵原子差异过大，迭代结束条件受步长波动影响较大，导致重构信号时出现丢失信号时变特征情况，同时由于重构步长非自适应造成运行时间过长。表1中DCT算法与KSVD ROMP算法重构信号平均运行时间为13.83s和10.28s。

而本文算法将稀疏系数矩阵中的特征向量进行归一化处理，将特征量缩放至[0，1]区间，将矩阵内所有特征系数归一化为同一数量级，简化了计算，从而提高运行速度。同时不断调整步长，改善算法迭代结束条件以提高信号重构精度。

3.3.2 压缩率与鲁棒性实验

为了验证本文KSVD NRAMP算法在不同压缩率下的有效性和鲁棒性，在不同压缩率下分别使用3种算法进行电能质量信号稀疏重构。选取重构信噪比（SNR）、均方误差百分值（MSE）作为评价指标进行对比分析。

图5为电能质量信号在压缩率为50%～90%时，3种算法的重构信噪比（SNR）曲线，图6为压缩率为50%～90%时，3种算法的均方误差百分值（MSE）曲线。

图5 不同CR下的重构SNR曲线

图6 不同CR下的重构MSE曲线

由图5、图6可知，对于电能质量信号，当压缩率（CR）在50%～90%时，本文所提算法与DCT算法和KSVD ROMP算法比较，重构信噪比（SNR）高出26～28dB，且均方误差（MSE）也明显小于其它两种算法。由此可知，本文所提算法在保持高压缩率状况下，不仅很好地保留了电能质量信号特征，改善了信号重构性能，完全满足电能质量信号分析要求，还可保证强鲁棒性。

3.3.3 实验结果对比分析

为更好验证本文算法的有效性及普适性，针对9种常见电能质量扰动信号各进行200次实验，取平均实验结果如表2所示。

由表2可知，當使用本文算法重构电能质量信号时，9种重构信号的信噪比SNR均在50dB以上，能量恢复系数EPR稳定高于99.89%，很好地保留了原始信号绝大部分能量，且均方误差MSE极小，进一步验证了本次实验的有效性和正确性。

4 结语

本文提出的KSVD NRAMP稀疏重构算法通过归一化稀疏矩阵原子，将特征向量缩放，缩小稀疏矩阵原子差异，加快函数收敛速度，提高了算法重构精度，减少了算法运行时间，可以很好地用于电能质量信号重构。该算法在迭代过程中，根据信号特征不断调整步长，保证了算法在高压缩率下的鲁棒性。同时利用奇异值分解不断更新字典，保留型号特征，避免了算法迭代残差计算时造成的误差。由实验可知，当压缩率（CR）在50%～90%时，本文所提算法重构信噪比（SNR）高达54dB～81dB，鲁棒性强。将该算法与电能质量信号识别结合，为电能质量信号检测与分析提供了一种新思路。

参考文献：

[1] UTKARSH S， SHYAM N S. Detection and classification of power quality disturbances based on time frequency scale transform[J]. IET Science， Measurement & Technology， 2017，11（6）：802 810.

[2] 祁兵，张丽坤，杨秋霞.一种新的电能质量自适应滤波方法[J].计算机应用研究，2008，25（1）：306 308.

[3] 张逸，林焱，吴丹岳.电能质量监测系统研究现状及发展趋势[J].电力系统保护与控制，2015，43（2）：138 147.

[4] 贾清泉，于连富，王宁，等.原子稀疏分解算法在电力系统扰动信号分析中的应用[J].电力系统保护与控制，2010，38（19）：17 21.

[5] WANG X， TIAN L， GAO Y X， et al. Analysis of power quality disturbance signal based on improved compressed sensing reconstruction algorithm[C].2017 IEEE Transportation Electrification Conference and Expo， Asia Pacific （ITEC Asia Pacific）， 2017：1 5.

[6] 黄建明，瞿合祚，李晓明.基于短时傅里叶变换及其谱峭度的电能质量混合扰动分类[J].电网技术，2016，40（10）：3184 3191.

[7] SANGEETA L M， VINAYAK N S. Comparative analysis of power quality using wavelets for real time implementation[C]. 2016 IEEE 7th Power India International Conference （PIICON）， 2016：1 4.

[8] 田振果，傅成华，吴浩，等.基于HHT的电能质量扰动定位与分类[J].电力系统保护与控制，2015，43（16）：36 42.

[9] KAVITA K， ATUL K D， OM P M. Detection of power quality disturbances in the utility grid with solar energy using S transform[C].2016 IEEE 7th Power India International Conference （PIICON）， 2016：1 6.

[10] ZAKARYA O ， VINCENT C ， YASSINE A， et al. Disturbances classification based on a model order selection method for power quality monitoring[J]. IEEE Transactions on Industrial Electronics， 2017，64（12）：9421 9432.

[11] SAQIB M A， SALEEM A Z. Power quality issues and the need for reactive power compensation in the grid integration of wind power[J]. Renewable and Sustainable Energy Reviews. 2015，43（1）：51 64.

[12] BU YAN， TIAN LIJUN， GAO YUNXING， et al. Load modeling based on power quality monitoring system applied compressed sensing[C].2017 IEEE Transportation Electrification Conference and Expo， Asia Pacific （ITEC Asia Pacific）， 2017：1 6.

[13] MANIKANDAN， SABARIMALAI M， SAMANTARAY， et al. Simultaneous denoising and compression of power system disturbances using sparse representation on overcomplete hybrid dictionaries[J]. IET Generation Transmission & Distribution， 2015，9（11）：1077 1088.

[14] 曲正偉，郝婉茹，王宁.原子分解快速算法在电能质量扰动分析中的应用[J].电力自动化设备，2015，35（10）：145 150.

[15] MANIKANDAN M S， SAMANTARAY S R， KAMWA I. Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries[J]. IEEE Transactions On Instrumentation & Measurement， 2015，64（1）：27 38.

[16] 高周亚同，王丽莉，蒲青山.压缩感知框架下基于K 奇异值分解字典学习的地震数据重建[J].石油地球物理勘探，2014，49（4）：652 660.

[17] DONOHO D I. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52（4）：1289 1306.

[18] 高悦，臧明相，郭馥英.基于小波变换和压缩感知的语音信号压缩研究[J].计算机应用研究，2017，34（12）：3672 3674.

[19] 尹宏鹏，刘兆栋，柴毅，等.压缩感知综述[J].控制与决策，2013，28（10）：1441 1445.

[20] ELAD M，AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing，2006，15（12）：3736 3745.