改进ANFIS ABC算法研究
2018-02-12张涛张轩雄
张涛 张轩雄


摘要:模糊规则提取和隶属度函数学习是模糊推理系统设计过程中重要而困难的问题。针对该问题,提出一种基于人工蜂群算法(ABC算法)训练自适应神经模糊推理系统(ANFIS)的新方法。神经网络采用5层ANFIS网络结构,并且描述了基本思想和算法实现过程。在ANFIS中引入ABC算法进行参数训练和优化,该方法适用于非线性系统辨识。实验结果表明,加入ABC算法之后,ANFIS训练和参数优化等取得了良好效果。
关键词:人工蜂群算法;群体智能;自适应神经模糊推理系统;均方根误差
Research on ANFIS Based on Artificial Bee Colony Algorithm
ZHANG Tao, ZHANG Xuan xiong
(School of Optical Electrical and Computer Engineering,
University of Shanghai for Science and Technology, Shanghai 200093,China)
Abstract:The extraction of fuzzy rules and the study of membership function are important and difficult problems in the design process of fuzzy inference system. To solve this problem, a new method of training adaptive neural fuzzy inference system (ANFIS) is introduced, which is a branch of swarm intelligence: artificial bee colony algorithm. The neural network adopts five layers of ANFIS network structure, and explains the basic idea and the realization process of the algorithm. In the adaptive neural fuzzy inference system, artificial bee colony algorithm is introduced to carry out parameter training and optimization. The proposed method is suitable for nonlinear system identification. The experimental results show that after the ABC algorithm is added, good results are obtained for ANFIS training and parameter optimization.
Key Words:artificial bee colony; swarm intelligence; ANFIS; RMSE
0 引言
自適应神经模糊推理系统(Adaptive Network Fuzzy Inference System,ANFIS)是一种将模糊系统与神经网络结合起来的新型模糊推理系统结构。它建立在模糊推理系统基本模型基础上,混合最小二乘法以及反向传播算法进行参数调整,并且能够自动产生if-then规则。一直以来,ANFIS参数的更新和训练都是重要难题之一。
近年来,许多新方法被用于优化隶属度函数。Shoorehdeli等[1]提出用于ANFIS训练的不同混合方法,结合粒子群算法、递归最小二乘法和扩展卡尔曼滤波用于其训练。Chatterjee等[2]描述了Takagi-Sugeno型模糊神经系统的发展过程,并将其用粒子群优化之后用于机器人动态建模。Chen[3]介绍了一种用于商业问题预测的混合ANFIS模型,结合粒子群算法与减法聚类。Turki等[4]提出一种用粒子群算法优化模糊神经系统的参数,通过使用粒子群算法调整与优化前提参数以及结论参数。Zangench等[5]提出一种用差分进化算法训练ANFIS的新方法。Catalao等[6]介绍了一种混合小波、粒子群优化以及ANFIS的方法用于短期电费预测。Gunesekaran 等[7]整合人工免疫算法和ANFIS,预测了印度国家证券交易所的预期指标值。Lin等[8]提出一种基于模糊熵聚类、改进粒子群算法以及递归奇异值分解的新的混合学习算法。
粒子群算法的局部寻优能力较差,需要较长的计算时间,而且容易陷入局部最优,不能绝对保证搜索到全局最优解,容易陷入局部最优解,稳定性较差。DE算法对参数设置的依赖性过强,设置不当会加长寻优时间,并容易陷入局部最优解。而人工蜂群算法参数较少,对于初始值的设置无特殊要求,算法适应性更强,可以采用串行和并行等多种方式实现,能够更好地与实际问题相结合。因此,本文提出一种利用人工蜂群算法训练ANFIS的新方法。该方法可以将ANFIS的参数训练过程近似转换为人工蜂群算法寻找最优解过程,通过人工蜂群算法调整训练参数,使ANFIS训练达到更好效果。该方法被应用于非线性系统辨识中,并且使ANFIS训练取得了良好效果。
1 自适应神经模糊推理系统
自适应神经模糊推理系统(ANFIS)是Jang[9]在1993年提出的。在复杂系统建模和控制方面,ANFIS效果相当不错,目前在许多方面已经有了成功应用,如函数拟合、控制系统辨识、模式识别、自适应噪声消除等。如谢苗等[10]介绍了一种基于改进型ANFIS的矿用空压机故障诊断系统,蒋磊磊等[11]介绍了一种基于Sugeno模糊模型的ANFIS应用于手势识别中。
1.1 表示形式
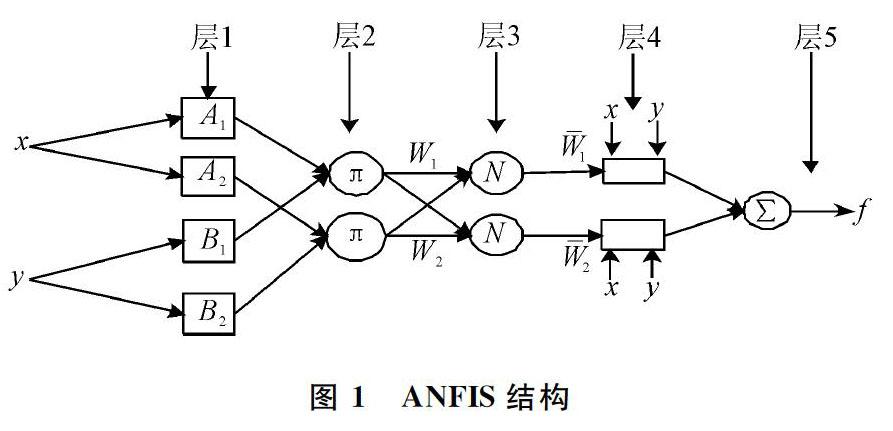
在模糊系统中,模糊模型的表示主要有两种:①模糊规则的后件是输出量的某一模糊集合,称为模糊系统的标准模型,即Mamdani模型;②模糊规则的后件是输入语言变量函数,典型情况是输入变量的线性组合,称为模糊系统的Takagi Sugeno模型。与Mamdani型相比,Takagi Sugeno型模糊推理具有利于分析、计算简单的优点,且容易与PID控制方法以及自适应方法结合,从而实现具有优化与自适应能力的控制器或模糊建模工具。Takagi Sugeno模糊模型主要由两部分组成:前提部分和结论部分,两部分彼此之间通过模糊规则相互联系。ANFIS的训练和更新主要针对该两部分。ANFIS结构由5部分组成,假设所考虑的模糊推理系统有2个输入和1个输出,则模糊规则形式为:
规则1:如 果x是A 1并且y是A 2,那么f 1=p ix+q 1y+r 1。
规则2:如果x是A 2并且y是B 2,那么f 2=p 2x+q 2y+r 2 。
1.2 模型结构
该模型的等效结构如图1所示。
第一层为模糊化层,它为每一个输入产生隶属度函数。隶属度函数可以是高斯函数或三角形函数等类型,如果为高斯函数,隶属度函数的两个可调参数分别为MF的中心c和宽度σ。该层的可调参数被称为前提参数。高斯函数公式如式(1)所示。
第二层为规则层,可以取任意的模糊T范式函数,一般情况下取所有输入信号的乘积。具体如式(2)所示。
第三层为归一化层。具体如式(3)所示。
第四层为去模糊化层,每一个节点是一个有节点函数的自适应节点,参数被称为结论参数。具体如式(4)所示。
第五层为输出层,计算所有输入信号的和。具体如式(5)所示。
总输出=∑w if i(5)
2 人工蜂群算法
2.1 算法简介
近年来,随着群体智能的发展,遗传算法、粒子群算法等相关算法被广泛用于解决各类问题,并进入许多学者的研究领域。人工蜂群算法(Artificial Bee Colony Algorithm,ABC算法)是Karaboga[12]在2005年根据蜜蜂觅食行为提出的优化算法,具有自适应、自组织、自学习等特征,并且被应用于函数优化[13-16]、组合优化、神经网络训练等多个领域。人工蜂群算法的提出和改进,为其进一步发展和使用發挥了十分关键的作用。宁爱平等[17]利用随机过程理论,给出ABC算法的Markov链模型定义等相关理论,并根据随机算法的收敛准则,验证了人工蜂群算法的全局收敛性。很多群体智能算法开始提出时,理论基础薄弱,因此从理论上分析和证明群体智能算法的收敛性是至关重要的,也有利于更好地推进算法改进和后续进一步提高性能。
自然界中的蜂群有雇佣蜂和非雇佣蜂两种,雇佣蜂也被称为采蜜蜂,而非雇佣蜂可以分为侦察蜂和跟随蜂。雇佣蜂和跟随蜂的主要任务是开采食物源,而侦察蜂的主要任务是寻找新的食物源。人工蜂群算法是根据自然界中不同蜂群的功能及其相互转换关系设计的一种新型群体智能迭代算法。在蜂群算法中,采蜜蜂数量是群体总量的一半,另一半是观察蜂。每一处食物源对应一个采蜜蜂,即采蜜蜂与食物源的数量相等。
ABC算法中的每一个循环搜索过程都有以下3个步骤:①将采蜜蜂、观察蜂和蜜源一一对应,并计算蜜源的丰富程度;②确定侦察蜂;③蜜蜂根据自身或者外界信息搜索蜜源。
种群参数有以下3个:①蜜蜂总数N(一般定义采蜜蜂和观察蜂的数量相等,即都为N/2);②最大迭代次数maxCycle(每次迭代中都有一次全局搜索和局部搜索);③蜜源停留最大限制搜索次数Limit(局部搜索Limit次,蜜源未更新,则采蜜蜂、观察蜂转化为侦察蜂)。
2.2 算法流程
(1)初始化。
(2)重复以下过程:①将采蜜蜂与蜜源一一对应,并且确定蜜源的花蜜量;②观察蜂根据采蜜蜂所提供的信息选择蜜源,同时确定蜜源的花蜜量;③确定侦察蜂,然后搜索新的蜜源;④记忆到目前为止最好的蜜源。
(3)判断条件是否成立。
在初始化阶段,食物源是根据每个给定边界范围的参数随机产生的。侦察蜂搜索新蜜源的操作如式(6)所示。
其中, k为不同于i的蜜源,j为随机选择的下标, ij为[-1,1]之间的随机数,它控制着x ij邻域内蜜源的随机位置,称之为人工蜂群算法的搜索方程。在算法的每一次迭代过程中,每一个采蜜蜂通过式(6)选 出与目前食物源位置最近的食物源,并且从原蜜源位置产生一个新的候选位置。
在某只采蜜蜂的位置周围,当搜索次数达到一定阈值Limit且还没找到更好的位置时,就会重新随机初始化采蜜蜂位置。随机初始化公式如式(7)所示。
式(7)中, i=1…SN,j=1…PN。SN是食物源的数量,PN是优 化参数的数量。
观察蜂主要根据适应度函数值的大小选择蜜源,适应度函数如式(8)所示。
当前蜜源位置经过采蜜蜂和观察蜂多次循环搜索之后,若没有提高效率,就会被蜜蜂放弃。此时,采蜜蜂就会转换为侦察蜂,然后随机搜索一个新的蜜源替换原来的蜜源。ABC算法主要包含4个过程:①观察蜂根据一定的选择概率选择蜜源,称为全局选择过程;②采蜜蜂与观察蜂结合局部信息在邻域搜索并产生候选位置,称为局部选择过程;③所有人工蜂对于新旧两种蜜源进行对比,保存优质蜜源;④侦察蜂搜索新蜜源,称为随机选择过程。
3 基于ABC算法的ANFIS
ANFIS有兩种类型参数:前提参数和结论参数。其中,前提参数属于隶属度函数参数,其总参数是所有隶属度函数的参数总和;结论参数用的是ANFIS的解模糊化层参数。
在ABC算法中,蜜源位置就是优化问题的一个可能解,每个解是一个D维向量,D是优化问题参数的个数。也就是说,每一个食物源的变量个数依赖于每一个输入输出的隶属度函数参数个数。其中,双边高斯型隶属度函数用于输入层,线性隶属度函数用于输出层。当使用ABC算法对这些参数进行训练时,采用均方根误差作为训练效果的评价指标。基于ABC算法的ANFIS要求其结构的均方根误差最小。均方根误差计算如式(9)所示。
其中, y 1i是模糊模型的预测值,y 2i是观测值,s是输 入训练数据对数。基于ABC算法的ANFIS模型如图2所示。
4 实验仿真及结果
在ABC算法控制参数的选取上:种群规模大小为20,食物源数量等于种群规模大小的一半,也就是10。Limit设置为100,也就是说,若某个雇佣蜂采蜜的食物源位置经过100次迭代后都没有进行更新获得改进,即该花蜜处的食物源花蜜数量都未获得改善,此时雇佣蜂放弃当前食物源,并且变成侦察蜂重新搜索新的食物源。将最大循环迭代次数设置为2 000。在本文中,采用单输入单输出训练数据集进行ANFIS ABC算法的数据处理及仿真,并且验证算法的可行性。训练数据集由式(10)定义,定义输入变量 x 的取值范围为[-1,1],并且随机产生50组训练数据集和50组检验数据集。
ABC算法应用于5个隶属度函数,5个隶属度函数都采用双边高斯型隶属度函数。经过ANFIS ABC算法进行2 000次迭代训练之后,均方根误差(RMSE)的变化趋势如图3所示,训练数据和检验数据在输入空间上进行均匀采样的输出曲线如图4所示。
本文利用ANFIS ABC算法对输入输出数据集进行训练,以RMSE作为评价标准,ANFIS ABC把训练过程转化为寻找最优解的过程。使用ANFIS ABC的RMSE训练结果为0.000 879,而使用ANFIS的RMSE训练结果为0.001 786。使用ANFIS ABC的RMSE预测结果为0.000 853,而ANFIS的RMSE预测结果为0.001 705。均方根误差显著减小,表明ABC算法在对ANFIS优化中的拟合能力和预测能力有显著提高,而加入ABC算法之后ANFIS在时间效率上低于ANFIS,如何提高效率是算法改进的重点。
5 结语
本文将人工蜂群算法用于自适应神经模糊推理系统参数的训练和更新。结合模糊推理系统及神经网络各自属性的自适应神经模糊推理系统在智能预测以及参数优化等方面有着广泛应用。为了解决模糊规则提取和隶属函数学习难题,引入人工蜂群算法在优化以及训练方面的优点。通过基础理论分析以及仿真实现验证,成功地将人工蜂群算法用于自适应神经模糊推理系统,并且取得了良好效果,充分证明了ANFIS ABC算法的可行性及有效性。
参考文献:
[1]
SHOOREHDELI M A, TESHNEHLABM,SEDIGH AK. Training ANFIS as an identifier with intelligent hybrid stable learning algorithm based on particle swarm optimization and extended Kalman filter [J]. Fuzzy Sets and Systems, 2009,160:922 948.
[2] CHATTERJEE A,WATANABE K. An optimized Takagi Sugeno type neuro fuzzy system for modeling robot manipulators [J]. Neural Computing & Applications, 2006,15(1):55 61.
[3] CHEN M Y. A hybrid ANFIS model for business failure predictionutilizing particle swarm optimization and subtractive clustering [J]. Information Sciences, 2013(220):180 195.
[4] TURKI M, BOUZAIDA S, SAKLY A, et al. Adaptive control of nonlinear system using neuro fuzzy learning by PSO algorithm[C]. 2012 16th IEEE Mediterranean, 2012:519 523.
[5] ZANGENCH A Z, MANSOURI M, TESHNEHLAB M, et al. Training ANFIS system with DE algorithm [C]. IEEE 2011 Fourth International Workshop, 2011:308 314.
[6] CATALAO J P S, POUSINHO H M I, MENDES V M F. Hybrid wavelet PSO ANFIS approach for short term electricity prices forecasting [J]. IEEE Transactions on Power Systems, 2011,26(1):137 144.
[7] GUNASEKARAN M, RAMASWAMI K S. A fusion model integrating ANFIS and artificial immune algorithm for forecasting indian stock market [J]. Journal of Applied Sciences, 2011,11:3028 3033.
[8] LIN C J, HONG S J. The design of neuro fuzzy networks using particle swarm optimization and recursive singular value decomposition[J]. Neurocomputing, 2007,71(1):297 310.
[9] JANG JSR. ANFIS adaptive network based fuzzy inference system[J]. IEEE Trans on Smc, 1993,23(3):665 685.
[10] 谢苗,刘治翔,毛君.基本改进型ANFIS的矿用空压机故障诊断系统[J].电子测量与仪器学报,2015(4):500 507.
[11] 蒋磊磊,秦丽娟,李武举.基于Sugeno模糊模型的ANFIS在手势识别中的应用[J].微型机与应用,2016(24):50 53.
[12] KARABOGA D. An idea based on honey bee swarm for numerical optimization [R]. Kayseri, Turkey: Erciyes University, 2005.
[13] KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm [J]. Journal of Global Optimization, 2007,39(3):459 471.
[14] KARABOGA D, BASTURK B. A comparative study of artificial bee colony algorithm [J]. Applied Mathematics and Computation, 2009,214(1):108 132.
[15] KARABOGA D, AKAY B. Artificial bee colony (ABC), harmony search and bees algorithms on numerical optimization [C]. Proc of Innovative Production Machines and System Virtual Conference,2009.
[16] KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm [J]. Applied Soft Computing, 2010,8(1):687 697.
[17] 寧爱平,张雪英.人工蜂群算法的收敛性分析[J].控制与决策,2013(10):1554 1558.
