反思“追及与相遇问题”的课堂教学

黄海亮

摘要：长期处于背、套公式的物理解题模式中的初中生，进入高中后随即暴露出初中方法习惯与高中物理学习之间的矛盾，这在学习直线运动的“追及与相遇问题”显得尤为突出。本文笔者将从两个简单、基础的直线运动追及相遇案例分析学生对这类问题难懂、妥协、放弃的原因，并根据本校老师的课堂效果谈谈个人感受，力争从高一开始就解决“病根”，而不是等到高三再亡羊补牢。

关键词：高中物理;追及;相遇

一、“追及与相遇问题”的解题思路

“追及与相遇问题”是匀变速直线运动中的难点，不少同行和各种资料也都各自总结了该问题的处理方法，大致可以概括如下：

（1）一个切入点：速度相等，它是追赶者能否追上或两者距离最大、最小的临界条件。

（2）两个等量关系：时间关系和位移关系，通过画草图找出两物体的时间关系和位移关系是解题的突破口。

（3）根据两者的时间关系和运动形 式，建立运动速度和运动距离两个方程，然后再看题中是否还能建立其它限制类方程。

（4）最后解方程，作必要分析。

一般情况下，我们也是按上述方法引导学生处理“追及相遇问题”，即“一个切入点和两个关系”;但很多学生没理解“一个切入点和两个关系”的具体含义，只知其一不知其二，此类题只要稍微拔高，学生就会望题生畏。究其根源，笔者认为是学生对基本、简单的追及运动情景分析、理解不够。针对这一个难点，我们在新授课上就必须引起足够的重视，以便帮助学生分析“追及相遇问题”的运动情景。下面以两个案例对该难点进行剖析和突破。

二、案例分析

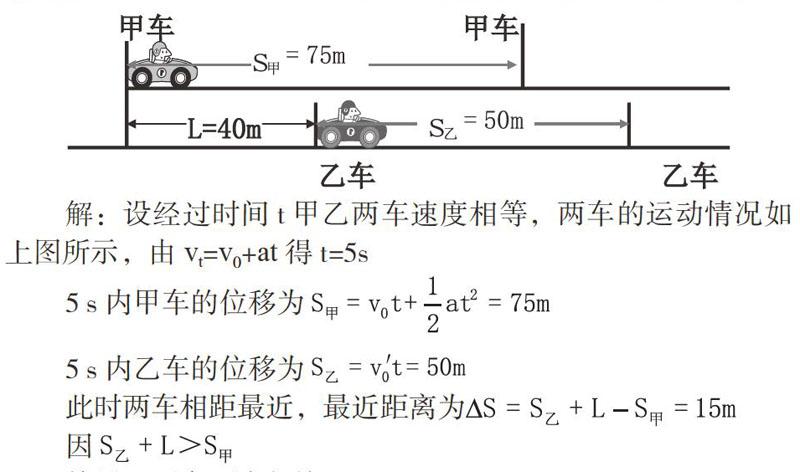
案例1：甲车以20m/s的速度在平直公路上运动，发现前方40m处有乙车以10m/s的速度同方向匀速行驶，便立即刹车，加速度大小为2m/s2，问：甲乙两车是否会相撞？若不会相撞，它们什么时候相距最远或最近？此时距离是多少？

这是典型的匀减速追匀速，因为学生初次接触，先不要着急解决题目后面的问题，我们需要设置一些问题或者画运动草图来详细地引导学生逐步分析运动情景，加深对此类问题的理解，特别是关于“切入点”的理解。下面引导学生分步处理该题：

第一步：讨论与交流

问题1：若甲车以5m/s的速度匀速行驶，则两车的间距____;（变大、不变、变小）

问题2：若甲车以10m/s的速度匀速行驶，则两车的间距____;（变大、不变、变小）

问题3：甲车以20m/s的速度匀速行驶，则两车的间距____;（变大、不变、变小）

这一步抛开题设，思考不同的速度差会导致甲乙的距离如何变化，发散学生思维，起到入门效果。

第二步：独立分析

由题意可知甲乙两车的间距逐渐____，关于是否相撞，可分以下情况讨论：

（1）若甲车的速度降至与乙车速度相等时，甲车仍未追上乙车，则甲乙两车____

思考：此种情况下，以后还会不会相撞？为什么？

（2）若甲车的速度降至与乙车速度相等时，甲车恰好追上乙车，则甲乙两车____

（3）若甲车的速度降至与乙车速度相等时，甲车已超过乙车，则甲乙两车____

该步是建立在第一步的基础上提问的，让学生理解怎样才会相撞，分析问题（1）和（3）背后所隐藏的运动情景，自然地得出相撞的临界条件，即我们的解题的切入点。

第三步：建立解题模型

（1）关于两车是否相撞的问题，解题的切入点是________

（2）当两车速度相等时，根据两车的运动类型和题设条件，找出两车从开始到速度相等时的时间关系和位移关系，并画出此过程的运动示意图。

（3）根据示意图判断当两车等速时，是否已经相撞或者刚好相撞？若未相撞，此时两车的距离最远（近）？距离是多少？

解：设经过时间t甲乙两车速度相等，两车的运动情况如上图所示，由vt=v0+at得t=5s

5 s内甲车的位移为

5 s内乙车的位移为

此时两车相距最近，最近距离为

因

故甲乙两车不会相撞

这里还可以让学生尝试用图象求解，利用图象求解追及相遇问题往往显得更加简洁。当然本文的关注点是高一新生如何更好地建立追及相遇问题的运动情景、理解我们解题常用的“一个切入点和两个关系式”，所以对于图象解法这里不再赘述。

第四步：总结归纳（巩固学习、方便记忆）

匀减速追匀速，当两车速度相等时，两车______。

案例2：一辆红色出租车10m/s的速度闯红灯，停在路口的警车发现后便以5m/s2的加速度追赶，问：（1）追上前辆车何时相距最远，最远距离是多少？（2）何时警车追上出租车，此时警车速度是多少？

第一步《思考与分析》

①开始时，两车速度谁比较大？说明开始一段时间内两车的间距在变大、变小还是不变？

②随着警车不断加速，当两车等速时，两车相距最远还是最近？

③在②之后，誰的速度更大？此后两车的间距在不断的变大、变小还是不变？

④当警车追上出租车时，两车的位移是何关系？

在案例1的基础上设置四个问题让学生独立分析另一种追及相遇模型，分析方法与案例1类似，通过递进式问题来强化学生对此类问题的运动情景理解，然后画出运动过程示意图，找到“一个切入点、两个关系式”进行求解。

解：

（1）设经过时间t两车速度相等，由得t=2 s

2 s内警车的位移

2 s内出租车的位移

此时两车间距最大，最大间距为

（2）设进过时间t'警车追上出租车，此时两车的位移相等

代入数据解得 （舍去）

此时警车的速度为

此处同样可以让学生尝试用图象法求解，感受不同方法的优缺点。

第二步：总结归纳

匀加速追匀速，当两车速度相等时，两车______。

在所有追赶运动中，当两车速度相等时，两车______。

这一步让学生自我总结提升，得到上述结论，然后引导学生归纳“追及相遇问题”的解题思路和方法：

（1）紧抓“一图三式”：过程示意图，时间关系式、速度关系式（切入点）和位移关系式。

（2）审题应抓住题设的关键字，充分挖掘题设隐含条件，如“刚好”、“恰好”等，找到临界条件，明确临界状态。

三、小结

由于篇幅原因，本文仅以两种最简单的追及相遇类型为例介绍了如何引导学生逐步建立此类问题的运动模型、理解“一个切入点和两个关系式”，还有诸如运动时间不等、二次相遇等更难的追及相遇问题并未罗列分析;但是笔者认为，若学生能独立分析基础、简单的“追及相遇问题”，理解“一个切入点和两个关系式”的具体含义，以后不管面对何种类型的追及相遇问题，学生都将能快速找到解题的突破口;而不是事倍功半的照搬解题套路，我们要力争从根源上突破难点，改变学生望题生畏和一遇新题望而却步的局面。最后，本文的各种看法和观点都是基于对本校学生情况提出的，如有不当之处敬请批评指正。