丝杆移动型爬杆机器人的机构设计与分析

张兆龙，孙金风，胡亮



丝杆移动型爬杆机器人的机构设计与分析

张兆龙，孙金风*，胡亮

（湖北工业大学 机械工程学院，湖北 武汉 430068）

夹持式机器人已成为主要的攀爬机器人，其两端手臂对攀爬对象夹持的安全性与可靠性是机器人重要的前提条件。丝杆移动型爬杆机器人的攀爬过程分为手臂台升降、身体复位和绕杆检测三个阶段。首先对机器人前两个阶段的丝杆进行受力分析，确定整机设计参数；再通过ADAMS对机械臂与杆的夹持过程进行动力学分析，根据机械手加速度曲线优选最佳受力时间，进一步分析各杆的角加速度，确定整机的可靠性；最后将机械臂简化为梁单元，进行有限元非线性屈曲分析，验证梁的安全性，并对携带传感器的机械臂进行优化，减轻重量。

爬杆机器人；丝杆；动力学分析；有限元分析

随着社会的发展，高空作业成为越来越普遍的工作。各种杆或管体在人们生活中的应用越来越广泛，如水、天然气管道和电线、路灯杆等[1]。当前需要一种能够在杆上爬行的机器人来代替人工攀爬来完成高空作业。其一方面，可以提高工作效率；另一方面，也使人们从危险、恶劣的工作环境中解脱出来。现在已有一些爬杆设备是通过气或液压传动来提供动力[7]，但两者都需要控制线路来传递动力，受到工作条件和能源输送的极大限制。随着机器人技术的发展，设计一款能在各种杆件上实现上杆、抱杆固定、下杆运动且能对杆壁进行检测、维修的机器人是十分迫切的[5-6]。

1 爬杆机器人的结构

现有机器人的运动方式中，腿式机器人越障能力强，承载能力大，机动性好，具有很强的壁面适应能力[8-9]，但其同样有结构复杂的缺点。如图1所示，研究设计出的一种丝杆移动型爬杆机器人通过丝杆传动来实现机器人的各个腿部间歇移动，完成往复爬杆的功能，且结构十分简单。

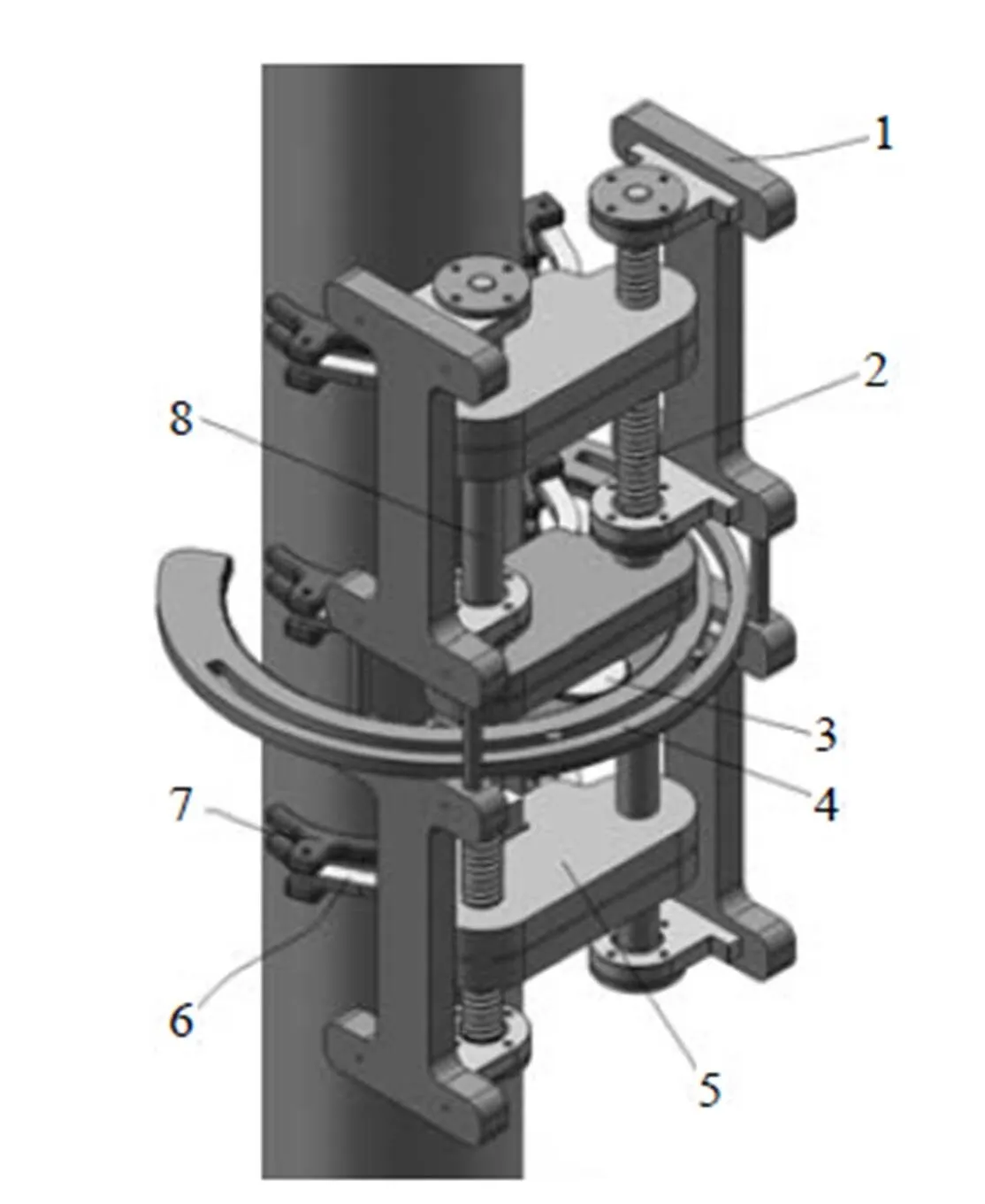
1.支撑架 2.丝杆 3.外齿轮 4.内齿轮 5.手臂台 6.机械臂组 7.机械手 8.光杆

本结构采用模块化设计，分为上中下三个模块，各模块之间具有自身的独立性，而且更换方便，降低了维修成本，保证了模块的经济性。三个模块之间共同协作，确保了机器人稳定的工作。

机器人上下模块都包含左右两个支撑架1，支撑架的轴承座上分别安装丝杆2和光杆8，手臂台5通过直线轴承和丝杆螺母分别安装在两杆上，机械臂组6由连杆连接齿轮臂和机械手7，调节杆一端安装在手臂台上另一端固定在连杆上，且中间滑槽上安装滑杆，滑杆另外一端连接机械手7。机器人的上、下两个模块采用左右交错安装，三个模块都含有手臂台，且中间模块放置主控和内啮合齿轮的检测装置。

机器人放置在杆上时，电机控制不完全齿轮的传动，使中间和下部模块的手臂抱紧杆壁，这时主控驱动上部电机带动丝杆旋转，上部模块的手臂台在另一端光杆的导向作用下实现稳定向上平动，当上升至最高行程点时，上部手臂台抱紧杆壁，然后下部模块的手臂台通过相同的方式向上移动。当上下模块的手臂台分别到达最高的行程点且抱紧杆壁时，中间模块的机械臂张开，通过上、下两电机反向旋转，使机器人身体复位（相对手臂台回到起初位置），行成一个向上爬行的运动周期。在上述反向控制下同理完成机器人的反向爬行。

机器人在运动阶段可以通过中间模块的外齿轮带动啮合的内齿轮转动，内齿轮上的传感器绕杆实现圆周检测，通过主控将数据传回操作者计算机。

2 爬杆机器人设计分析

机器人运动行程＝130 mm，为了更好地实现手臂台的移动，避免工况下外界的干扰[3]，增加抗压能力15%，则整体机器人的质量为＝10 kg，其中手臂台的质量0＝2.1 kg。机器人工作时手臂台在丝杆上运动，丝杆副受到轴向载荷作用，在丝杆公称直径0处产生螺纹力矩M。当机械手臂台中丝杆螺母无预紧情况下，即有：

式中：0为丝杆受到总力矩，N·m；M为在丝杆公称直径0处产生螺纹力矩，N·m；0为丝杆公称直径，mm；F为丝杆副受到的轴向载荷，N；0为丝杆导程，mm；为螺纹传动效率。

图2 丝杆与工作台受力图

由式（1）可知，电机对丝杆产生的扭矩转化到手臂台上的力1，得：

根据螺纹副的计算，图2（a）和（b）两种方式分别是螺母A对丝杆B的压力和丝杆B对螺母A的压力。两物体之间摩擦系数相同，则ρ1＝ρ2。

机器人运动的主动力为电机驱动丝杆转动，当丝杆顺时针运动时，螺母相对于丝杆有向上运动的趋势，其受力为式（2）。而当身体上升时，丝杆则与螺母上端面接触，产生压力，由式（3）可知，其产生的轴向力相对于前者，需要产生的驱动力更大，即需要的转动扭矩更大。手臂台作用到丝杆的力F为：

由受力分析确定整机尺寸为325×260×520 mm，结合式（1），1＜2，由后架总重量选择电机为57步进电机。而电机运动时，丝杆对手臂台承载的作用力分解为水平分力和竖直分力，电机驱动丝杆，对手臂台产生的水平分力是对系统有害的分力，则采用光杆作为导向，和丝杆的配合，使手臂台平稳地上升。

3 手臂台工作的运动分析

为满足机器人在杆上稳定地升降运动，机械手对杆壁的夹持力满足其在杆上产生的摩擦力与机器人身体重力相互平衡[4]。因此需要在机械手弧面上添加一层橡胶，增大机械手与杆壁面之间的摩擦因数，进而增大摩擦力。防止机器人在攀爬过程中受到倾覆作用，设计的三组机械手臂台在每个工作阶段都有两组夹持杆臂，实现手臂台和机器人身体交替式上下移动。

3.1 机械手臂的优化

机器人对杆壁面产生的作用力为机械手对杆的挤压力，因而两者都会产生一定的变形，这种形变根据ADAMS进行优化分析得到最优值[2]，以实现机器人对杆壁施加不破坏两者之间的压力，且满足机器人在杆壁上爬行的作用。基于拉格朗日方程式对机械手的各个零件运算得到各自的运动曲线。

式中：＝－，为拉格朗日函数；为系统总动能；为系统总势能；q为广义坐标；Q为广义坐标下对应q的惯性力，N。

机械手对壁面产生力的方向，集中指向杆截面圆的圆心时，对壁面的夹持力为最佳范围，如图3，但不同时刻产生的形变是不同的。如图4，通过ADAMS实验仿真多个不同时刻，来确定加速度得到机械手不同受力情况，求解得到产生的作用影响最小，即确定机械手产生夹持力最佳的情况。

1.杆 2.机械手 3.连接杆 4.调节杆 5.滑杆 6.齿轮臂 7.机械手臂台

图4 不同时刻机械手加速度变化曲线

由图数据可知，当齿轮臂产生1.5 rad/s的转速，机械手臂的加速度变化，由多个时刻的动力学测试，得到6.08 s时壁面产生的压力为最合适值，其上下浮动值都会产生过大的加速度，发生显著振动，影响机器人整体的运行。

根据上述的最优解，测量齿轮臂的角加速度，如图5所示，其中起伏较大的两处为开始接触杆壁和对杆壁施加最大作用力时候的状态，两者中间的部分产生的平稳波动为机械手靠近杆的状态，其切向加速度由于在接触过程中，产生阻碍机械手运动的作用反力，随着机械手与壁面的接触面逐渐增大，因而表现波动。其前后两个状态的最大值不超过1.5×10-7rad/s2，运动缓慢，确保了机器人夹持杆的安全性。

结合图6，滑杆为了适应机械手靠近杆时的加速度，与调节杆产生相对运动，将其传递给手臂台，降低机械手夹持杆的挤压力。开始阶段，滑杆推动机械手靠近杆，表现为正方向；而在结束阶段约束滑杆，产生作用反力，作用在调节杆上，则其加速度曲线上表现出一正一反两个方向的加速度。且整个分析过程中各零件加速度曲线浮动稳定，无过大受力波动，满足实际要求。

图5 齿轮臂运动的角加速度变化曲线

图6 调节杆的加速度变化曲线

3.2 机械手臂的校核

每个机械臂含有上下叠加的两个机械手，且每次工作有两组机械手夹持杆壁。考虑到机械手与杆之间采用面接触,夹持产生的摩擦力需要支撑机器人身体的重力，即有：

手臂台移动时，电机的输出功需克服手臂台与丝杆的摩擦损耗和机器人身体的重力势能。

结合式（4），电动机驱动丝杆，使机器人到达预定位置所需的时间＝13 s；摩擦耗为w，J；电动机的功率为0，W；转矩为0，N·m；为移动的高度，mm。则有：

结合式（5）～式（8）计算得到需要驱动丝杆运动的电极转矩0＝6 kg·cm。

4 机械手结构的有限元分析

上述手臂台的动力学分析满足机器人正常工作，能够承载对壁面施加一定的力，本节整体分析机器人的夹持后的状态，来验算机械臂对整体的支撑。

4.1 机械手非线性屈曲分析

机器人在运行过程中一直存在机械臂与杆接触状态，当机器人夹持杆件准备运动时受力最大，且连接臂变形量最大，运用有限元分析软件ANSYS对此进行承载受力分析[5]，根据得到的机械臂变形的挠度判断合理性。

从机构所能容纳的空间考虑，机械臂在除了沿着手臂的方向，其他方向上的变化很小，可以将其简化为一个等截面悬臂梁的受力情况。简化后，得：

1＝100，＝12，＝8

式中：1为机械臂的长度，mm；为截面的长，mm；为截面的宽，mm；I为矩形截面对轴的截面惯性矩，cm4；W为长方形截面对轴的抗弯截面系数，cm3。

弧形的机械臂是为了更加节省空间，使得机器人结构显得更加紧凑。从屈曲分析结果可知，在多个的机械臂抱紧杆壁的状态下，产生形变量十分微小。

结合式（9）、式（10）可知机械臂的端点处挠度为：

结合图7，当连接臂末端承受最大承载力＝25 N时，机械手臂处于悬臂状态，最大挠度值＝0.23181 mm，两者计算符合实际的误差范围，满足要求。

图7 机械手臂受力加载云图

非线性屈曲分析时，首先对简化梁进行静力学结构分析，通过屈曲分析得到负载因子，然后利用ANSYS中UPGEOM命令对模型施加初始缺陷，再根据零件受到的静态载荷，将其线性屈曲模态变形乘以因子0.0001后，更新机械手臂的几何形状，通过绘制力与位移的曲线，得到手臂的非线性临界载荷为0.5×104N。

4.2 机械手结构的优化设计

机器人手臂采用多个梁单元组成，为得到真实的截面应力和变形，在ANSYS中采用Beam188单元进行优化。当机械臂上携带大量传感器，增大了机械手臂的负载，因此可将其等效为一个变截面梁。

优化过程中，输入参数1、2、3分别为梁第一、二、三截面宽度，输出参数4、5、6分别为梁质量、总变形结果、等效应力。

由图8（a）可知，参数2超过17.6后，再进一步增加对5（最大应力）产生的影响较小，可知2变化范围在16.5～18 mm之间。而图8（b）中1、2和3在总变形0.128～0.145 mm之间，变形范围小，具有优化空间。

图8 参数之间的响应图

根据候选设计点，插入到设计空间后，由原来的0.15 kg，在不影响机械臂的等效应力的情况下，优化各个截面的宽度，减轻重量到0.13124 kg，而整机中安装有3组手臂台，共6个机械臂，总重量减轻了0.11256 kg，减轻手臂的重量。

5 结论

（1）机器人整体设计采用三个自主独立模块，三个模块之间交替工作，完成攀爬的三个工作状态：手臂台升降、身体复位和绕杆检测。且每个工作过程中都具有两组机械手臂台夹持杆壁，来实现稳定地攀爬过程。

（2）利用丝杆与光杆共同作用对爬杆机器人进行结构设计，并对不同阶段丝杆与机械手臂台上螺母之间进行受力分析，进而调整整机的结构，并确定设计参数。

（3）利用ADAMS对机械手臂夹持过程进行了动力学分析，确保机械手在对杆壁均匀施加压力区段内获得最大有效值，检测机械手各杆的角加速度，其结果满足整机工作要求，并存在很大的优化空间。

（4）采用ANSYS对机械臂进行非线性屈曲分析，施加初始缺陷，多次试验运算得到机械臂的临界载荷。对于复杂工况下，机械臂上携带传感器时，进行优化设计，减轻结构重量，使机械臂负载得到了优化。

[1]江励，管贻生，周雪峰，杨铁牛，苏满佳，吴鸿敏. 双爪式爬杆机器人的夹持性能分析[J]. 机械工程学报，2016（3）：34-40.

[2]李楠，纪小刚，徐凯，崔爱强. 一种适应不同导杆直径的多姿态爬杆机器人[J]. 现代制造工程，2011（9）：58-61.

[3]王才东，范国锋，王新杰，汤一明. 一种自锁式爬杆机器人的设计与分析[J]. 机械传动，2015（10）：60-63.

[4]彭力明，高志勇，陈磊，叶文亚. 一种多滚轮框架式爬索机器人的设计与分析[J]. 机械设计，2014（4）：24-26，54.

[5]杨萍，王彦云. 阶梯攀爬机器人行走机构的设计与动力学分析[J]. 机械设计与研究，2016（2）：51-53，59.

[6]段宇，侯宇. 轮式管外攀爬机器人结构设计与动力特性分析[J]. 机械设计与制造，2016（12）：17-20.

[7]王蕾，陆小龙，赵世平，曹志华，刘晓宇，梁恩志. 电力铁塔攀爬机器人直线推杆机构设计与分析[J]. 机械设计与制造，2012（3）：52-54.

[8]周克东，王进戈，柳在鑫，等. 丘区农机仿生助力腿的动力学仿真与分析[J]. 机械设计与研究，2013（4）：36-39.

[9]魏晓霞，蒲小琼，冯常. 基于水下爬行机器人的机械手结构设计[J]. 机械，2015，42（4）：77-80.

Mechanism Design and Analysis of Screw Climbing Robot

ZHANG Zhaolong，SUN Jinfeng，HU Liang

( School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China )

The clamping way has become a major climbing robot,and it is an important prerequisite for the robot to satisfy the safety and reliability of the arms when climbing. The climbing process of the screw climbing robot is divided into three stages: arm movements, body reset and detect around. Firstly, the force analysis of the screw in the robot first two stages is carried out to determine the design parameters of the whole robot. Then the kinetics analysis of the clamping process of the arm and the pipe is carried out by ADAMS, according to the acceleration. The optimal time is obtained according to the acceleration curve of the manipulator, and the angular acceleration of each rod is further analyzed to determine the reliability of the whole robot. Finally, the finite element nonlinear buckling analysis is carried out to verify the safety of the beam, and the arm carried the sensor is optimized to reduce the weight of the robot.

climbing robot；screw；dynamic analysis；finite element analysis

TP242.3

A

10.3969/j.issn.1006-0316.2018.01.014

1006－0316 (2018) 01－0066－06

2017－05－15

国家级大学生创新创业训练计划项目经费资助（201510500002）

张兆龙（1995－），男，湖北武汉人，本科，主要研究方向为机械设计及其自动化。

通讯作者：孙金风（1979－），男，湖北鄂州人，工学硕士，副教授，主要研究方向为机器人技术、机械设计及理论。