决策树法在化学事故救援兵力编组中的应用

沈同强 周华任 彭文亮 张鑫鹏 陈宪

近年来，随着化学工业的高速发展，我国危险化学品事故呈现出高发频发态势，严重危害着人民生命财产和生态环境安全[1]。化学事故发生通常比较突然，救援难度大。救援界认为，在“黄金72小时”内，灾民存活率极高[2]。军队和武警防化分队作为重要的专业救援力量，在处置化学事故中发挥了突出作用。天津港“8·12”特大火灾爆炸事故发生后，防化救援力量迅速到位、果断处置，积累了丰富经验的同时，我们也认识到，当前由于军队和武警救援分队专业人员及装备等力量相对比较薄弱且分布不均匀，指挥员必须要在事发后的短时间内作出最佳救援决策，合理安排兵力编组，才能最大限度减少伤亡，提升救援效果。

决策树法是运筹学中一个重要的理论分支,它的基本功能是用树形结构描述备选方案、自然状态和收益值之间的随机因果关系[3]。决策树法适合解决较复杂的风险型决策问题，尤其是对那些需要逐次进行决策的“多级决策问题”更为有效，具有思路清晰、形象直观、便于计算等优点[4]。军队和武警参与灾害救援过程中，可灵活运用决策树法，在确定救援兵力编组上辅助决策。

1.分兵编组与集兵编组的确定

化学事故发生一般比较突然，前期随着有毒有害物质的扩散和人员的自救互救，通常最初时段死亡人数增长较快，但随着时间推移，死亡总体人数虽仍继续上升，但增速变缓，类似于正态分布曲线。如遇事故地点或受灾群众不在一处的情况，指挥员就需要在最短的时间内定下决心作出决策，合理安排兵力编组。具体哪一种方案能使伤亡人数预期达到最小值，指挥员不能简单依靠经验或意愿，这时可以借助决策树法进行辅助验证。

例如，某化工厂因中控平台操作不当，造成相邻两个厂区（记为地点A和地点B）化工设备同时出现故障，进而剧毒气体扩散到附近居民区，伤亡人数不断上升。假定随着时间的推移人员的死亡人数预期值参考表1。武警某防化中队接到上级命令，迅速对这两个厂区实施救援。三地成三角形分布，各相距30km，预计两点间机动时间均为1h。由于救援中队兵力及配套装备极少，只能组成10个救援小组。指挥员经过慎重研究，认为可以采取2种救援方案：

方案1：将救援队分成2个分队，每个分队有5个救援小组，分别前往两个厂区实施救援；

方案2：集中全部救援力量，形成优势兵力，依次对两个厂区实施救援。

两种救援方案所对应的救援时间如表2所示。（如分兵救援，到达第二个地点时伤亡人数按照前一地点完成时间加路途时间后起算。例如，在地点A救援使用了2h，机动到地点B途中用去1h，则在地点B救援使用了1h完成救援的话，地点B伤亡人数参照4h的死亡人数。下同。）请分析确定救援中队应采取哪种救援方案才能使周边群众伤亡人数期望值达到最小。

根据以上决策问题的有关信息，可绘制决策树，如图1所示。

表1 随时间推移周边群众伤亡情况

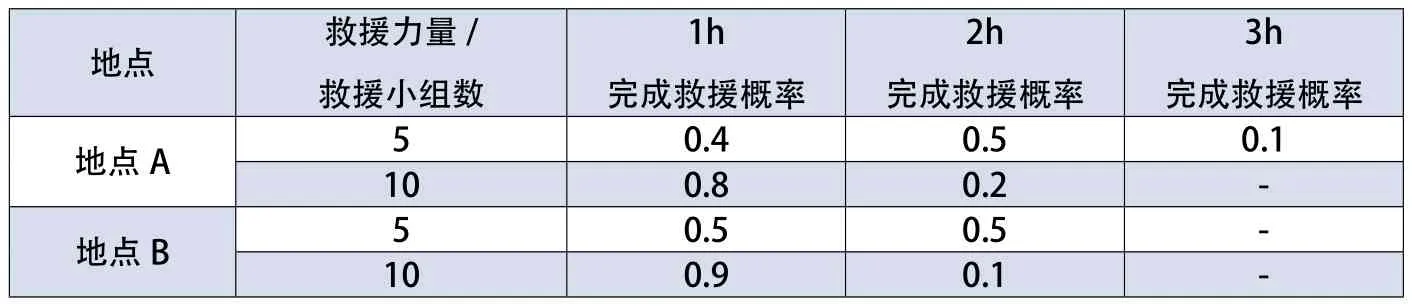
表2 完成化学事故救援任务的时间及相应概率

表3 决策树用到的三种符号

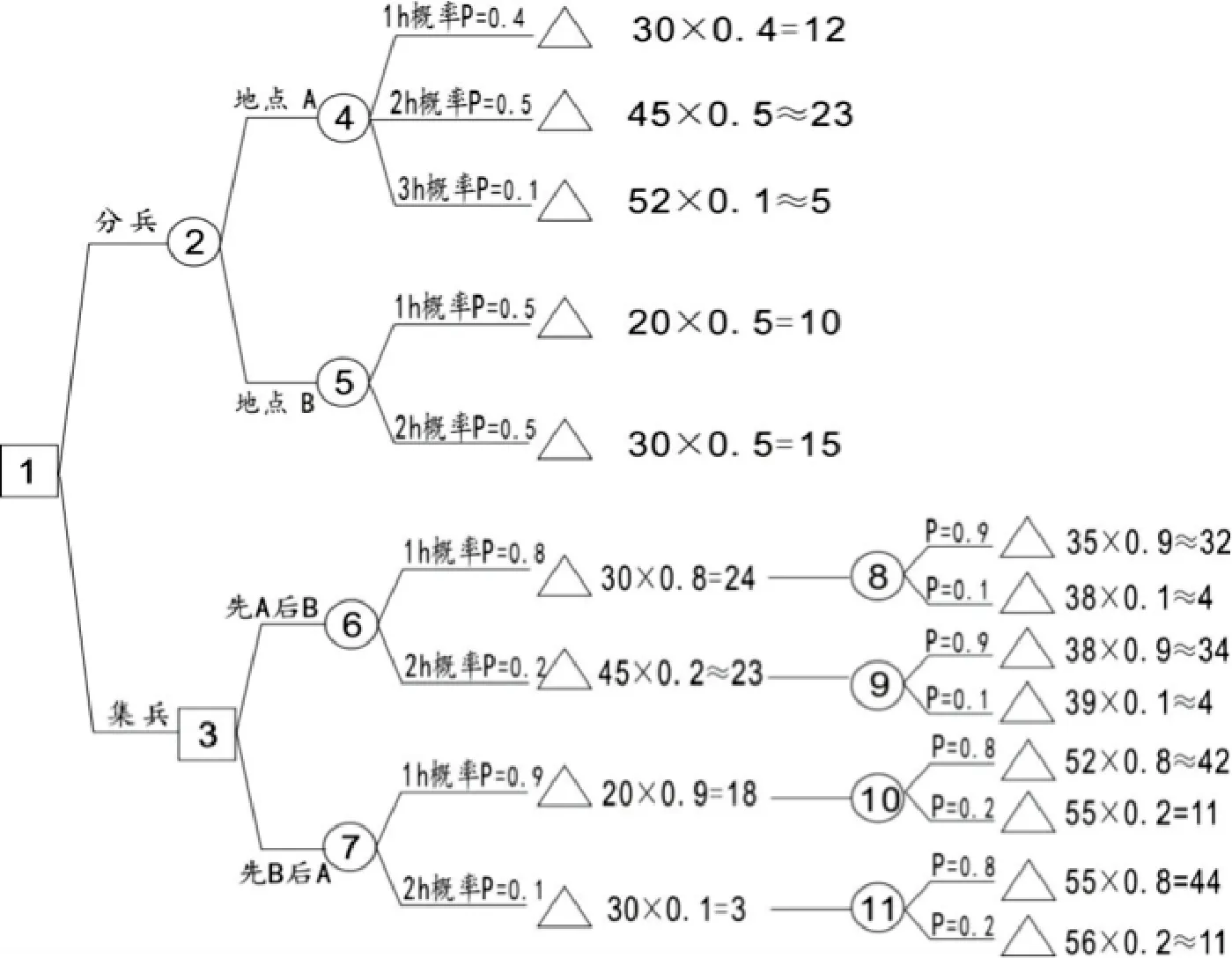
图1 合兵与分兵决策树

依据决策树，可以直观形象地计算出各节点伤亡人员期望值，进而确定最终决策方案：

据此，可得出结论，应将救援分队分兵两路，分别前往地点A和地点B实施营救，这样周边群众伤亡预期值最小，为65人。

当然，题目中所给出的例子不能代表所有情况，现实当中如果两地相距较近，救援队机动不会造成明显的时间浪费，根据“N-平方率”中关于“有效战斗力与战斗单位数的平方成正比”的规律[5]，兵力编组情况则应考虑“集中优势兵力”，救援效率才会更高。实践运用中救援队指挥员要根据现场情况灵活应对，科学决策。

2.平均编组与侧重编组的确定

在救援编组确定时，不但有“分”与“合”的区别，还涉及到具体如何分组的问题。当事故厂区周边群众人数和救援效率不同时，编组也应随之变化。例如，设地点A处于城镇，受灾人员比较多，但相对集中，救援难度较小；而地点B处于分散的乡村，受灾人员较少，且救援难度较大。这时平均分组实施救援，与侧重于地点A处适度增加的救援力量相比，死亡预期值将会相差多少呢？

假定地点A、B随时间延长伤亡人数如表4所示，完成救援任务时间及相应概率如表5所示。

方案1：将救援队平均分为2个分队，每个分队分别有5个救援小组，同时开往地点A和地点B开展救援；

方案2：将救援队分为2个分队，其中地点A处安排6个救援小组，地点B处安排4个救援小组；

根据以上决策问题的有关信息，绘制决策树，如图2所示。

依据决策树，计算出各节点伤亡人员期望值，进而确定最终决策方案：

E(4)=15+23+16=54人

E(5)=10+15+3=28人

E(2)=E(4)+E(5)=82人

E(6)=9+23+10=42人

E(7)=8+15+6=29人

E(3)=E(6)+E(7)=71人

E(1)=min｛E(2)，E(3)｝=71 人

据此，可得出结论，应将救援分队兵分两路，在受困人员相对密集且救援难度相对较小的地点A处适度增加救援力量，安排6个化学救援小组，在地点B处安排4个小组，可使泄漏厂区周边群众伤亡预期值最小，为71人，较之平均分组伤亡预期人数少了11人。

表4 随时间推移毒气泄漏造成群众伤亡情况（人）

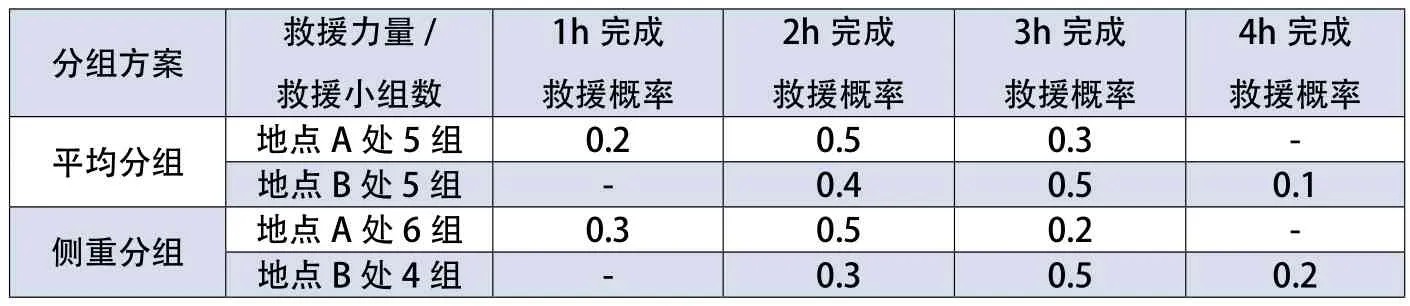
表5 完成化学事故救援任务的时间及相应概率

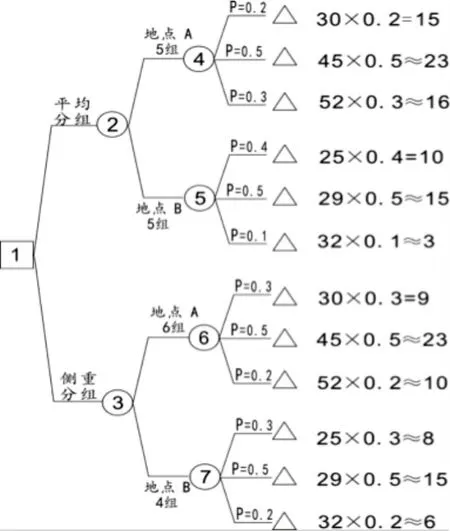
图2 平均与侧重决策树

3.结论

本文通过两个利用决策树法辅助制定兵力编组问题的例子，演示了决策树法在辅助决策时的应用过程。当然，在实际救援当中，现场情况复杂，参数给定要依托指挥员丰富的经验和准确的判断，因此，指挥员应在平时加强对事故案例的研究，一旦有任务需要，能够在最短的时间内认真分析情况、准确判断形势、借助科学方法进行兵力编组、拟定救援方案，以求在化学事故救援中，用最合理的方案实现最大的救援效益。

[1]胡建明.化学事故应急救援战术战法探讨[J].武警兵种.总第135期.2016（1-5）.

[2]黄敏东.论海上遇险黄金救援时间[J].世界海运.第37卷第233期.2014（33-35）.

[3]周华任，赵颖，周生.运筹与优化[M].清华大学出版社.2012（233）.

[4]郑国用，高春生.应用军事运筹学方法辅助决策边防指挥决策[J].武警学院学报,第30卷第3期.2014（14）.

[5]徐长山，姜延军，林学俊.自然辩证法概论[M].国防大学出版社.2005（94）.