特高压直流分层接入电网的落点选择研究

翟海保, 李兆伟, 黄 慧， 吴雪莲， 罗凯明， 庄侃沁， 罗 峰

(1. 国家电网公司华东分部，上海 200120；2. 国电南瑞科技股份有限公司，江苏 南京210003；3. 南瑞集团有限公司， 江苏 南京210003；4. 国网江苏省电力有限公司，江苏 南京210024)

0 引言

近年来，我国特高压交直流输电工程应用取得了重大突破。华东电网作为我国最大的直流受端电网，截至2016年底，共有包含4回特高压直流在内的8回直流投入运行。如此密集的直流落点为电网的规划和运行带来了诸多挑战[1]，其中直流落点的选择是电网规划中需要解决的关键问题之一。按照国家电网公司规划，至2018年底华东电网还将新建3回特高压直流，为实现特高压直流功率输送的优化，引导潮流合理分布，部分新建直流工程将采用分层接入1000 kV及500 kV电网的方式运行[2]。由于特高压直流分层接入方式存在其特殊性，因此为直流落点的选择引入了新的约束[3-10]。

直流落点选择是一个非常复杂的系统决策问题，牵扯到决策目的、系统安全、经济性、工程实施等多方面。在目前大电网规划中，通常基于电网电力平衡需求，由规划设计人员直接制定有限数量的直流落点方案，在此基础上进行安全稳定性、经济性等方面的计算分析与评估，通过结果比较确定最终直流落点规划方案。这种评估方法能够同时考虑多种因素影响，但由于每个直流落点方案安全稳定性和经济性等评估工作量大，很难对所有可能方案进行评估比较，初始方案的制定在很大程度上需要依靠规划设计人员的工作经验，缺少对所有可能方案进行大面积初步筛选的工作环节和技术手段。文献[11]从有效短路比、静态电压稳定指标和有功功率损耗3方面提出了同时兼顾稳定性和经济性的直流落点选择方法，但在稳定性方面没有考虑多直流系统之间的相互影响因素，指标的设置较为简单，操作过程中应用性不强。文献[12]围绕直流多馈入短路比，着重深入考虑新增直流与已有直流系统的交互影响，为直流落点选择提供决策支持，但根本上该方法仅基于直流短路比，未考虑其他影响因素，结果可能较为片面。

为解决特高压直流分层接入的落点选择问题，文中基于直流分层接入的特殊性，重点研究了直流分层接入的评价指标，指标涵盖了分层接入直流的运行特性、对已投运直流的影响、直流分层接入的潮流疏散特性以及系统稳定裕度。基于所提指标，采用多目标优化决策算法对不同直流分层接入方案进行决策，并以实际多直流落点规划电网为例，分析了所提决策方法的有效性，所得结论可为交直流电网规划提供方法和技术支撑。

1 特高压直流分层接入电网方式的特点

特高压直流分层接入受端电网的简化等值模型如图1所示[2]，特高压直流高端换流变、低端换流变分别接入500 kV和1000 kV网架，交流滤波器和无功补偿装置也分别接入500 kV和1000 kV交流母线。由于直流逆变侧同极的2个换流器阀组串联运行，而同一极的高、低端阀组分层接入2个不同系统参数和运行工况的交流电网，导致高、低端换流变参数(例如变比、漏抗、分接头调节步长等)完全不同，从而造成高、低端阀组的触发角、熄弧角和直流电压都有所差异。因此必须把分接头控制功能配置在阀组层，而不能放在极层中，以方便对两交流系统独立响应[3]，这客观上为各换流器功率的独立控制提供了条件，使直流分层输送到不同电压等级的功率控制更为灵活[4]。

由于直流分层接入受端电网不同电压等级落点间的电气距离一般都较小，因此某一电压等级换流站发生扰动可能会对另一个电压等级的换流站运行特性造成影响[3]。尤其是高端换流站和低端换流站之间的无功电压控制方面，某一电压等级系统的滤波器投切是否会对另一系统的滤波器投切造成扰动是关注的重点，在确定直流分层接入落点时应考虑这一因素的影响。

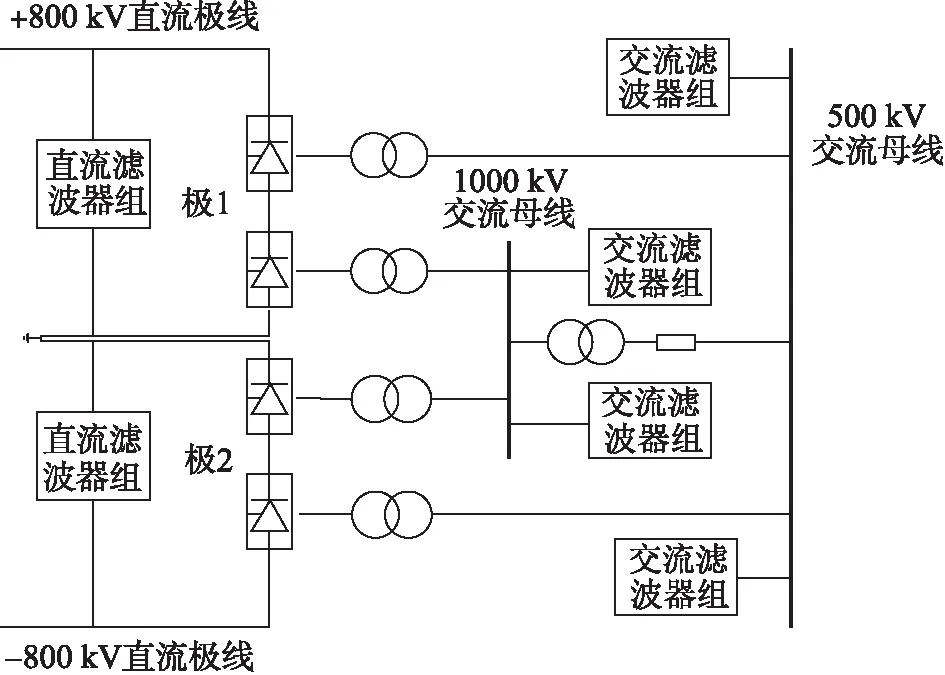
图1 特高压直流分层接入方式Fig.1 UHVDC hierarchical connection mode to AC power grid

2 特高压直流分层接入电网落点选择评价指标

现有针对多直流落点选择的研究很少。在目前交直流电网规划和直流输电工程前期论证中，通常事先根据经验预定几种直流落点方案，然后利用潮流和稳定程序对各方案进行安全稳定仿真计算，比较不同落点方案的稳定特性，在此基础上根据研究人员的经验确定满足系统稳定要求的实施方案建议，缺少定量有效的评价手段。

直流落点选择需要考虑多个不同技术领域，且各方面可能包括若干需要考虑的因素，因此在电网规划论证中，很难用数学方法描述不同方面的因素之间的关系，更难以设计一个同时兼顾上述因素的合理的决策方法。在工程实践中，比较简单的办法是首先在各专业技术领域中分别筛选出可能的合理落点方案；在此基础上，从不同领域的综合角度，比选获得最终的直流落点规划方案。文中结合特高压直流分层接入的特点，提出涵盖经济性和安全稳定性的多个评价指标，用于定量评价不同落点方案在各个方面的优劣程度，最终利用多目标决策算法从多个落点方案中选择优化的决策方案。

2.1 经济性指标

评价直流分层接入方案的经济性指标主要包括两部分。一是不同落点方案的工程造价Pbl，二是不同落点方案下系统网络损耗Ploss。工程造价方面，前文提到直流分层接入方式下某一电压等级换流站发生扰动可能会对另一个电压等级的换流站运行特性造成影响。为了降低这种影响，通常可采用适当增加分层接入点之间的电气距离的方法，这往往会造成工程造价的改变。网络损耗方面，由于直流落点不同会影响直流接入后的潮流分布特性，进而对系统网络损耗造成影响。但网络损耗与系统的运行方式密切相关，实际计算时选用多个典型方式下的平均值作为指标值。文中重点考虑电网稳定特性对特高压直流分层接入落点选择的影响，因此在后文算例分析时忽略工程造价差别。

2.2 直流分层接入短路比

直流采用分层接入方式，从系统来看，相当于将其分为2个容量一定的直流，再经换流母线分层接入1000 kV和500 kV，从短路比定义[10]的角度上其计算方式与直流单层接入方式并无区别，只不过分层接入的特高压直流需要对分层接入不同电压等级的2个换流站分别计算多馈入短路比，在形成全系统的节点导纳阵时需同时保留分层接入交流电网的1000 kV和500 kV换流站母线及其他直流换流站母线，直流分层接入的容量按实际容量计算。即分层接入直流第i层的多馈入短路比可由式(1)获得：

(1)

式中：Ri为分层接入直流第i层的多馈入短路比；Sac1为第i层换流母线交流侧的系统短路容量；UNi为第i层换流母线上的额定电压；Zeqii为等值阻抗矩阵中第i层换流母线对应的自阻抗；Zeqij为等值阻抗矩阵中第i层换流母线和第j回直流(包括直流分层接入的另一层)换流母线之间的互阻抗；Pdi为第i层直流的额定功率；Pdj为第j回直流(包括直流分层接入的另一层)的额定功率。

2.3 分层接入直流对已投运直流的影响

当电网中新投运直流时会对已投运的直流运行特性造成影响，从短路比来看会造成已投运直流的多馈入短路比下降。文献[12]在这一方面做了大量的工作，为了全面地分析新接入直流对已投运直流多馈入短路比的影响，提出了影响整体性指标、均衡性指标、干扰性指标、安全裕度指标，其基本思想是利用统计的观点从不同方面分析新接入直流对已投运直流多馈入短路比的影响。文中从“木桶理论”的角度选择直流分层接入后已投运直流的多馈入短路比最小值作为分层接入直流对已投运直流的影响指标，即为了保证系统安全稳定运行，首先应保证多馈入短路比最小的直流可以正常运行。至于其他已投运直流短路比下降对系统的影响，可通过后文中的系统稳定裕度予以考虑。假设电网中已投运直流的多馈入短路比为Mscr_n，则分层接入直流对已投运直流的影响指标F可表示为式(2)：

F=min{Mscr_n,n∈已投运直流}

(2)

2.4 直流分层接入后电网疏散能力

直流分层接入是应对特高压直流大容量接入受端电网后潮流疏散困难的有效手段，但即便分层接入大幅减少了直流注入到单一厂站的功率，若直流落点方案不合理仍可能由于多个疏散通道耦合造成特高压直流功率疏散困难。在此，疏散能力主要考虑两个指标：(1) 电网N-1故障或计及稳控策略的N-2故障约束下直流分层接入的最大能力Pmax；(2) 考虑直流额定接入输送容量下的为满足潮流疏散要求直流分层接入在不同电压等级上的功率分配比例Rd。其中直流最大输电能力要考虑直流设备的能力，如±800 kV特高压直流最大输电能力为10 000 MW。分层接入的功率分配比例方面，虽然直流分层接入采用阀组侧控制直流电流、电压和熄弧角可以灵活实现直流功率在高低端换流站的分配，但当高低端功率不相等时，必然导致同一极上高低端阀组的压降不同，若压降差别较大，可能影响直流阀组的寿命，评价疏散能力的指标Rd采用式(3)表示：

(3)

式中：PH为高低端4个阀组中输送功率最大的一个阀组功率；PL为输送功率最小的一个阀组功率，当每一极高低端输送功率相等时，Rd=1。

2.5 直流分层间交互影响程度

由于直流分层接入在受端电网的2个落点电气距离一般较小，因此在直流无功控制方面，某一层换流站的滤波器投切是否会对另一层的滤波器投切造成扰动是关注的重点，或者某一层换流站滤波器的投切会对另一层换流站的母线电压造成多大的影响，从影响的定义来看与多馈入直流相互作用因子基本一致[13]。因此，可以借鉴多直流相互作用因子定义直流分层间相互作用因子作为衡量直流分层间交互影响程度的指标Hi：当直流分层接入某一层换流母线i存在无功扰动，使其电压下降1%时，另一层换流母线j的电压变化为ΔUj，如式(4)。

(4)

式中：Ui0为换流母线i扰动前的母线电压；Zii为等值阻抗矩阵中换流母线i对应的自阻抗；Zij为等值阻抗矩阵中换流母线i和换流母线j之间的互阻抗。

2.6 系统暂态稳定裕度

直流分层接入后会对电网的安全稳定特性造成影响，不同的分层接入方案造成的影响不同。电力系统暂态安全稳定包括暂态功角稳定、暂态电压安全和暂态频率安全。暂态功角稳定裕度可基于标准的等面积扩展理论(extended equal area criterion，EEAC)计算获得；暂态电压安全包括暂态电压跌落可接受性和暂态电压稳定性；暂态频率安全裕度一般采用暂态频率跌落可接受性进行评价。这3个指标均可由集成了EEAC理论的FASTEST仿真软件通过时域仿真获得[14]。

单故障下安全稳定裕度为暂态功角稳定裕度、暂态电压安全裕度、暂态频率安全裕度中的最小值，备选方案下安全稳定裕度为所有考核故障下系统安全稳定裕度的最小值。系统稳定裕度一般通过时域仿真开展，但对所有可能存在的方案及故障进行扫描对比，工作量大，且不同方案下考核的故障往往存在差异。因此实际操作中为了提高效率及仿真对比的有效性，可将不同直流分层接入方案下系统薄弱断面输电能力作为系统稳定裕度指标η，通过比较系统薄弱断面输电能力的变化情况衡量分层接入不同方案对系统暂态稳定裕度的影响。

3 直流分层接入电网落点选择策略

直流分层接入方案优化是一个多目标决策问题，常用的多目标决策方法有目标规划法、多目标模糊决策法、逼近理想解排序法(TOPSIS法)等[15-20]。在决策的过程中，各项指标的权重有着十分重要的作用，权重是否合理直接决定了评价的科学性。权重的确定一般可以分为主观赋权法、客观赋权法以及组合赋权法3类。其中，主观赋权法包括层次分析法、德尔菲法等；客观赋权法包括熵权法、模糊聚类分析法等；组合赋权法是在综合主、客观赋权结果的基础上研究出来的复合型赋权方法，能较好地弥补主客观赋权法各自的缺点。文中利用德尔菲法与熵权法相结合的组合赋权方法确定各指标的权重，再采用基于灰色关联理论的TOPSIS法对直流分层接入方案进行决策优化。

3.1 指标权重的确定

由于每个评价指标的重要性往往不同，需要为每个评价指标确定一个权值来代表其对决策方案的影响程度，权值的科学合理性会直接影响优选的结果。德尔菲法和熵权法都是较为成熟的决策方法[16]。其中德尔菲法作为一种主观赋权法，不需要具备样本数据，主要依靠专家经验即可对评价指标的相对重要性作出判断；熵权法能较为客观地反映指标信息熵值的效用价值，但它需要样本数据，缺乏各指标之间的横向比较。

为了使权值既能反映决策者的主观愿望，又能体现决策的客观性，文中采用德尔菲法确定主观权重，熵权法确定客观权重，并以主客观加权属性值一致化为目标求取主观权重和客观权重的加权系数，进而得到组合权重。假设通过德尔菲法确定各指标的主观权重为ωDj，利用熵权法确定各指标的客观权重为ωej，利用德尔斐法与熵权法相结合的方法得到第j个指标的综合权重ωj为：

(5)

3.2 直流分层接入落点选择策略

各指标权重确认之后，通过计算不同直流分层接入方案下的指标值，即可采用基于灰色关联理论的TOPSIS法对直流分层接入方案进行决策优化。TOPSIS法的基本思想是：计算现实中的每个方案距离最佳方案和最差方案的距离，通过理想解的相对接近度作为综合评估的标准。利用灰色关联度进一步改进TOPSIS法[20]，可以更确切地表述备选方案与理想方案的贴和度，以此比较方案的优劣程度，最终提供决策依据。步骤包括：

(1) 首先计算所有备选方案的加权决策矩阵。

(6)

式中：vmn为第m个备选方案中第n个指标的标准化指标值。

(2) 根据各备选方案的指标值，确定所有备选方案的正理想解G和负理想解B。

(7)

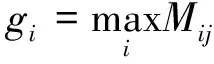
(3) 计算不同接入方案与正、负理想解的距离如下式所示。

(8)

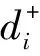
(4) 计算方案与正、负理想解的灰色关联度。

① 第i个方案与正理想解关于第j个指标的灰色关联系数为:

(9)

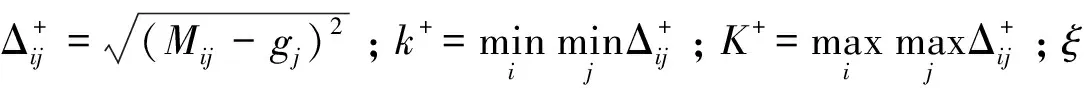
第i个方案与正理想解的灰色关联度为：

(10)

② 第i个方案与负理想解的灰色关联度计算类似，关于第j个指标的灰色关联系数为:

(11)

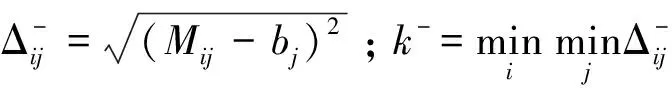
第i个方案与负理想解的灰色关联度为：

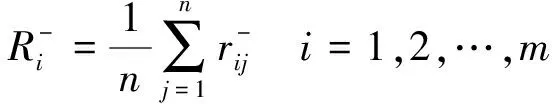
(12)

(5) 将备选方案与正、负理想解的距离和灰色关联度标准化。由于备选方案与正、负理想解的距离和灰色关联度的度量方法和数量级不同，需要进行无量纲标准化：

(13)

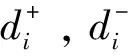
(6) 计算方案的相对贴近度。di′-和Ri′+数值越大，样本越接近理想解；di′+和Ri′-数值越大，样本越偏离理想解。综合考虑标准化的备选方案与正、负理想解的距离和灰色关联度，得到各方案与正、负理想方案的接近程度如下。

(14)

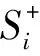
那么，各方案的相对贴近度为：

(15)

将所求的相对贴近度进行排序，贴近度越大，则方案越优。

4 算例分析

为了验证算法的有效性，基于实际电网中某规划分层接入的特高压直流开展落点选择研究。实际电网的局部简化网架如图2所示，其中实线为现有网架，共有7回单层接入的直流投运(图中局部电网仅画出一回直流，落点I变电站)，计及规划项目的可行性，规划的特高压分层接入方案有4种，通过虚线表示：当直流低端换流站接入ZZ1000 kV变电站时，直流高端换流站可通过方案1接入A、B、D 3个500 kV变电站或通过方案2接入B、C、D 3个500 kV变电站；当直流低端换流站接入YY1000 kV变电站时，直流高端换流站可通过方案3接入C、E、F 3个500 kV变电站或通过方案4接入C、E、F 3个500 kV变电站。发电厂J通过XX-YY特高压线路送出是该网架下的薄弱断面，系统稳定裕度选用XX-YY断面的输电能力。

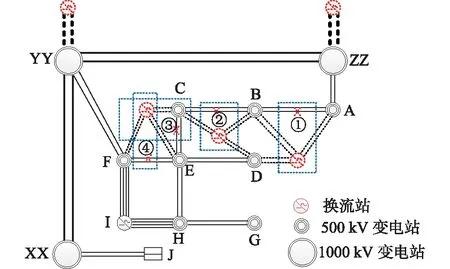
图2 某实际电网简化示意Fig. 2 Network structure diagram of scheme 1

针对上述各方案，基于实际电网的典型方式计算数据，可得各个方案下指标计算值如表1所示。根据各指标的计算值，首先运用德尔斐法、熵权法计算各指标的权重如表2所示。

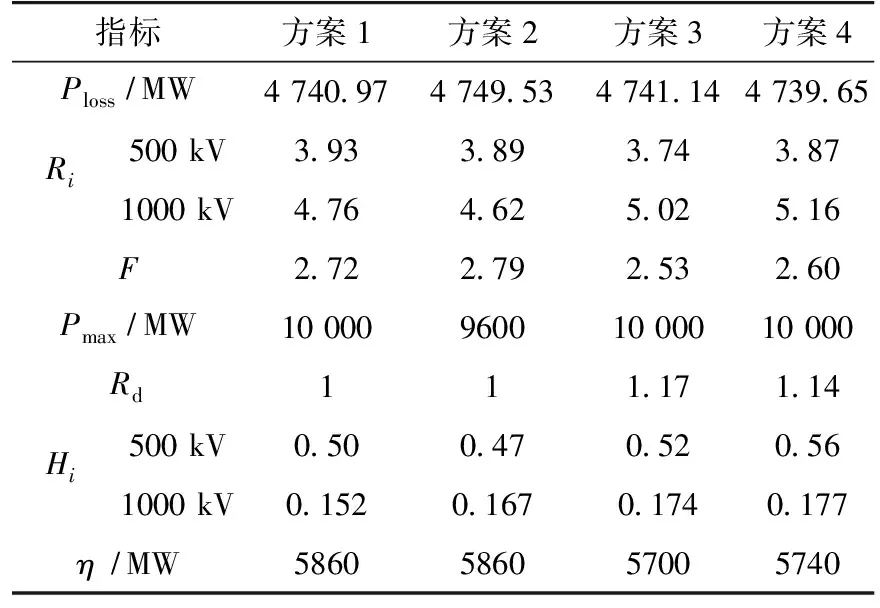
表1 各直流分层接入方案指标值Tab.1 Index value of all the schemes

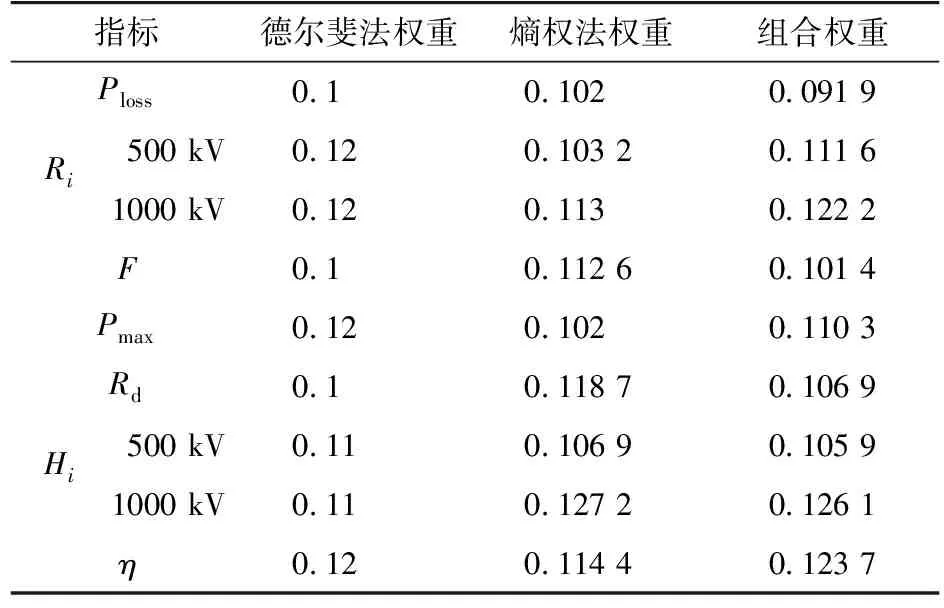
表2 各指标权重值Tab.2 Weights of all the indexes

基于灰色关联理论的TOPSIS法对4个备选方案进行决策优化。根据式(7—13)计算各备选方案与正、负理想解的标准化距离和灰色关联度，结果如表3所示。根据式(14)计算得到各备选方案与正、负理想解的接近程度如表4所示。

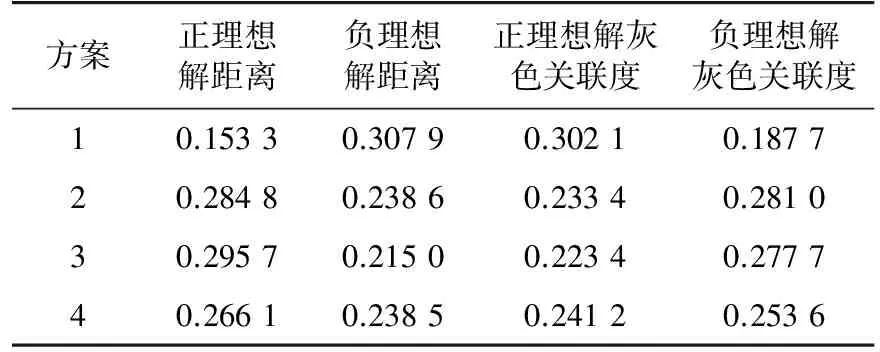
表3 各方案备选方案与正、负理想解的标准化距离和灰色关联度Tab.3 The normalized euclidean distance and greycorrelation degree of all the schemes

由式(15)计算得到各备选方案相对贴近度：方案1为0.641 4；方案2为0.454 8；方案3为0.433 3；方案4为0.479 9。由计算结果可知，方案1便是所给考核指标下4个方案中的最优方案，与实际规划相符。

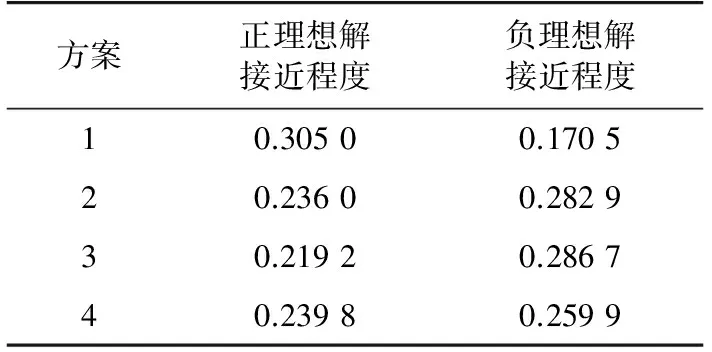
表4 各方案备选方案与正、负理想解的接近程度Tab.4 Closeness between all the schemes andthe positive or the negative ideal solutions

5 结语

文中从电网运行规划的实际需求出发，计及直流分层接入电网的特点及影响，建立了能较为全面地综合评价直流分层接入电网的多个指标，包括工程造价，系统网损、直流分层接入短路比、分层接入直流对电网已投运直流的影响、直流分层接入电网后疏散能力、直流分层间的交互影响程度以及系统稳定裕度，兼顾了电网经济性及安全稳定特性。针对不同的特高压直流分层接入方案，通过计算各指标值，然后利用基于灰色关联理论的TOPSIS法从备选方案中得到优化方案。通过在实际电网的应用，证明该方法具有工程实用性，可为特高压直流分层接入电网落点规划提供技术支撑。

[1] 李明节. 大规模特高压交直流混联电网特性分析与运行控制[J]. 电网技术,2016,40(4):985-991.

LI Mingjie.Characteristic analysis and operational control of large-scale hybrid UHV AC/DC power grids[J].Power System Technology,2016,40(4): 985-991.

[2] 刘振亚,秦晓辉,赵 良,等. 特高压直流分层接入方式在多馈入直流电网的应用研究[J]. 中国电机工程学报,2013,33(10):1-7.

LIU Zhenya,QIN Xiaohui,ZHAO Liang,et al. Study on the application of UHVDC hierarchical connection mode to multi-infeed HVDC system[J].Proceedings of the CSEE,2013,33(10):1-7.

[3] 李少华,王秀丽,张 望，等. 特高压直流分层接入交流电网方式下直流控制系统设计[J]. 中国电机工程学报,2015,35(10):2409-2416.

LI Shaohua, WANG Xiuli, ZHANG Wang,et al. Control system design for UHVDC hierarchical connection to AC grid [J]. Proceedings of the CSEE,2015,35(10): 2409-2416.

[4] 郭 龙,刘崇茹,贠飞龙,等. ±1100 kV直流系统分层接入方式下的功率协调控制[J]. 电力系统自动化,2015,39(11):24-30.

GUO Long,LIU Chongru,YUN Feilong,et al. Power coordination control of ±1100 kV UHVDC system with hierarchical connection mode[J].Automation of Electric Power Systems,2015,39(11):24-30.

[5] 吴彦维,李 晔,陈大鹏，等. 10 000 MW特高压直流工程受端分层接入交流电网方式下直流控制系统研究[J]. 电力系统保护与控制,2015,43(18):108-113.

WU Yanwei,LI Ye,CHEN Dapeng,et al.Research on control system for 10 000 MW UHVDC station B hierarchical connection to AC grid[J]. Power System Protection and Control,2015,43(18):108-113.

[6] 汤 奕,陈 斌,皮景创,等. 特高压直流分层接入方式下受端交流系统接纳能力分析[J]. 中国电机工程学报,2016,36(7):1790-1800.

TANG Yi,CHEN Bin,PI Jingchuang,et al. Analysis on absorbing ability of receiving AC system for UHVDC hierarchical connection to AC grid [J].Proceedings of the CSEE,2016,36(7):1790-1800.

[7] 汤 奕,陈 斌,王 琦,等. 特高压直流分层接入下混联系统无功电压耦合特性分析[J]. 电网技术,2016, 40(4):1005-1011.

TANG Yi,CHEN Bin,WANG Qi,et al.Analysis on reactive power and voltage coupling characteristics of hybrid system for UHVDC hierarchical connection to AC grid[J]. Power System Technology, 2016, 40(4): 1005-1011.

[8] 管永高,张诗滔,许文超. 特高压直流分层接入方式下层间交互影响研究[J]. 电力工程技术,2017,36(2):32-37.

GUAN Yonggao,ZHANG Shitao,XU Wenchao. Study on hierarchical interaction of UHVDC hierarchical connection mode [J]. Electric Power Engineering Technology,2017,36(2):32-37.

[9] 李虎成,袁宇波,卞正达,等. 面向特高压交直流大受端电网的频率紧急控制特性分析[J]. 电力工程技术,2017,36(2):27-31.

LI Hucheng,YUAN Yubo,BIAN Zhengda,et al. The frequency emergency control characteristics analysis for UHV AC/DC large receiving end power grid [J]. Electric Power Engineering Technology,2017,36(2):27-31.

[10] 朱鑫要,汪惟源,汪成根. 江苏特高压交直流输电交互影响研究[J]. 江苏电机工程,2016,35(2):39-42.

ZHU Xinyao,WANG Weiyuan,WANG Chenggen. Analysis of interaction between UHVAC and UHVDC for Jiangsu Power Grid [J]. Jiangsu Electrical Engineering,2016,35(2):39-42.

[11] 王 康,刘崇茹,韩民晓,等. 兼顾稳定性与经济性的交直流系统直流落点选择方法[J]. 电力系统自动化,2011,35(24):73-78.

WANG Kang,LIU Chongru,HAN Minxiao,et al.A method of selecting DC links termination at AC locations considering stability and economy at once[J].Automation of Electric Power Systems,2011, 35(24):73-78.

[12] 郭小江,郭剑波,马世英,等. 基于多馈入短路比的多直流落点选择方法[J]. 中国电机工程学报,2013,33(10):36-42.

GUO Xiaojiang,GUO Jianbo,MA Shiying,et al. A method for multi DC location selection based on MISCR[J]. Proceedings of the CSEE,2013,33(10):36-42.

[13] DAVIES J B.CIGRE WG B4.41 report:system with multiple DC infeed [R]. CIGRE Electra,2007.

[14] 李兆伟,刘福锁,李 威,等. 基于TOPSIS法考虑电力安全事故风险的运行规划分负荷方案优化[J]. 电力系统保护与控制,2013,41(21):71-77.

LI Zhaowei,LIU Fusuo,LI Wei,et al.Optimization of operating and planning load dispatching scheme considering the risk of electrical safety incidents based on TOPSIS method [J].Power System Protection and Control,2013,41(21):71-77.

[15] 马 平,游欣佩. 模糊多目标决策方法在风电场选址中的应用[J]. 可再生能源,2013,31(11):60-65.

MA Ping,YOU Xinpei.Application of fuzzy multi-objective decision-making method in wind farm site selecting[J].Renewable Energy Resources, 2013,31(11):60-65.

[16] 郭金维,蒲绪强,高 祥，等. 一种改进的多目标决策指标权重计算方法[J]. 西安电子科技大学学报,2014,41(6):118-125.

GUO Jinwei,PU Xuqiang,GAO Xiang,et al.Improved method on weights determination of indexes in multiple-objective decision[J].Journal of Xidian University,2014,41(6):118-125.

[17] 韩正伟,林锦国,邵如平. 模糊多目标决策理论在电能质量综合评价中的应用[J]. 继电器,2007,35(10):33-36.

HAN Zhengwei,LIN Jinguo,SHAO Ruping.Application of fuzzy multi-objective decision making theory in synthetical evaluation about power quality[J]. Relay,2007,35(10):33-36.

[18] 康世崴,彭建春,何禹清. 模糊层次分析与多目标决策相结合的电能质量综合评估[J]. 电网技术,2009,33(19):113-118.

KANG Shiwei, PENG Jianchun, HE Yuqing. Comprehensive evaluation of power quality based on the integration of fuzzy analytic hierarchy process with multi-objective decision-making[J].Power System Technology, 2009, 33(19):113-118.

[19] 梁飞强,彭显刚,梁志鹏. 基于DEMATEL-ANP-AEW-TOPSIS的配电网综合能效评估[J]. 广东电力,2016,29(1):31-35,64.

LIANG Feiqiang, PENG Xiangang, LIANG Zhipeng. Evaluation on comprehensive energy efficiency of power distribution network based on DEMATEL-ANP-AEW-TOPSIS[J]. Guangdong Electric Power,2016,29(1):31-35,64.

[20] 钱吴永,党耀国,熊萍萍,等. 基于灰色关联定权的TOPSIS法及其应用[J]. 系统工程,2008,27(8):124-126.

QIAN Wuyong, DANG Yaoguo, XIONG Pingping, et al. Based on the grey relation of fixed weight TOPSIS method and its application[J].System Engineering,2008,27(8):124-126.