含UPFC南京西环电网系统可靠性评估研究
2018-02-08刘国静胡晓燕朱鑫要
李 琥, 刘国静, 朱 磊,胡晓燕, 谈 健, 朱鑫要
( 1. 国网江苏省电力有限公司经济技术研究院, 江苏 南京 210008;2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103)
0 引言
统一潮流控制器(unified power flow controller,UPFC)是当前灵活交流输电技术发展的前沿产品,它能够同时调控系统的电压、阻抗及功角等参数,具有灵活控制潮流、提高电网传输能力及改善系统稳定性等多种功能[1-2]。2015年底,为解决南京220 kV西环网中关键输电断面输电能力不足、新的输电通道难以建设等实际问题,国网江苏省电力有限公司建成投运了世界首个基于模块化多电平(modular multilevel converter,MMC)技术的220 kV UPFC工程[3-4]。南京220 kV西环网UPFC工程投运一年多来,多次调整控制策略,缓解了南京西环网输电断面的重载问题,发挥了巨大的工程效用。
然而,目前关于南京西环网UPFC工程的研究中,更多的是从工程建设、运行分析等方面展开研究[5-9],对UPFC自身可靠性,尤其是对UPFC投运后对电网整体可靠性的影响分析还相对较少。文献[10]将UPFC三状态、四状态可靠性模型扩展到九状态,能够考虑UPFC降额运行、单换流器运行等运行方式,在此基础上建立UPFC灵敏度解析模型,能够更精确地获取UPFC停运概率。文献[11]分析了UPFC随机故障和不同的控制策略对系统失稳概率指标的影响,并基于非序贯蒙特卡洛模拟方法建立了分析流程,以修正EPRI-36节点系统为例进行仿真计算。文献[12]考虑了母线电压、线路潮流对UPFC停运概率的影响,在此基础上建立了含UPFC的负荷削减模型,可通过事故后的UPFC控制降低系统切负荷概率指标。为保障UPFC的可靠运行,实际中一般对其重要的子系统需配置备品、备件以减少故障停运时间,现有研究在UPFC可靠性建模中对备用元件的考虑尚不够充分。
随着后续电网发展,江苏电网必然会采用更多的柔性输电装置。然而,这些柔性输电装置的可靠性将不可避免的对江苏电网的可靠性带来影响。因此,有必要以南京西环网220 kV UPFC为研究对象,开展可靠性分析研究,为后续柔性输电装置在江苏应用提供借鉴分析。
1 南京220 kV UPFC工程概况
南京西环网主要由500 kV龙王山变电站和500 kV东善桥变电站从南北两端供电,区域内带有华能南京电厂、华润南京电厂等电源。西环网的供电范围包括主城西部、河西新城、奥体新城等,集聚了政府机关、高等院校等较多重要负荷。南京西环网地处南京中心城区,无论是新建输电通道还是对现有通道实施增容改造,均存在投资巨大、实施难度大的问题。为解决南京西环网潮流分布不均问题,2015年,国网江苏省电力有限公司建成了220 kV UPFC示范工程。该工程在220 kV晓庄—铁北双线上装设2×60 MV·A串联换流器,在220 kV燕子矶变电站35 kV母线上装设1×60 MV·A并联换流器,如图1所示。
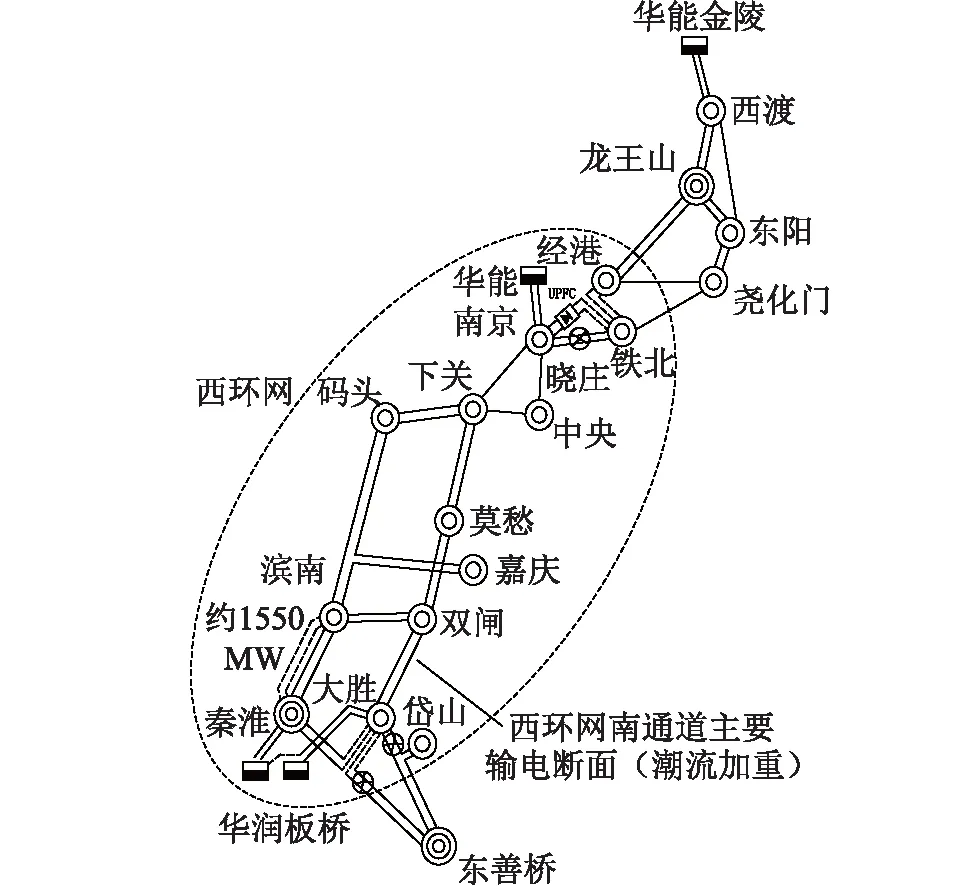
图1 UPFC安装位置Fig. 1 The installation location of UPFC
2 含UPFC可靠性评估
2.1 UPFC子系统可靠性模型
按照功能和连接关系,UPFC可划分为4个子系统:VSC换流桥子系统,主要有换流阀组、换流阀冷却设备及保护装置等;换流变压器子系统,包括单相三绕组换流变压器、交流侧断路器等;控制及保护子系统;极设备子系统,包括中性点接地支路及相关开关元件。
UPFC各子系统及组成元件是可修复的且每个元件的状态数是有限的,主要是运行、检修、安装3种状态,并且每个元件的寿命和修复时间都服从指数分布,可看作在空间上具有若干的离散可识别的状态且在时间上是连续的系统,因而可以用稳态马尔科夫过程来建模[13]。因此,可以按照容量水平建立子系统的状态空间图,同时也可将子系统的状态空间图组合成整个系统的状态空间图。
UPFC的重要设备结构复杂并且检修时间长,如果子系统中设备故障,整个系统可能将无法运行因而一些重要设备都有备用元件。对于各个子系统的建模需要考虑到备用的数量和所处的状态。
2.1.1 无备用元件的可靠性模型
不考虑元件备用时,可用状态转移图来模拟元件的运行、检修和安装3个随机过程。状态空间图如图2所示,其中,100%和0%分别表示元件处于100%容量状态和停运状态;1运行表示1个元件在运行,0备用表示没有元件处于备用状态,1和0分别是处于该状态的元件数;运行和备用表示元件所处状态;状态1,状态2表示元件处于不同的状态;λ为元件的故障率;μ为元件的修复率;γ为元件的安装率。λ,μ,γ单位均为次/a。

图2 不带备用的状态转移Fig.2 State transition diagram without backup
根据图2所示的状态转移图,无备用时元件的转移概率密度矩阵A如式(1)。
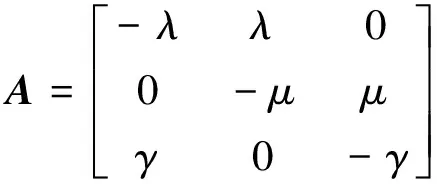
(1)
平稳状态概率满足:
(2)
式中:(p1,…,pN)为各个状态的概率。求解式(2),得到图中3个状态对应的稳态概率p1,p2,p3。进一步根据式(3—5)可求得元件等效可靠性参数。
λeq=λ
(3)
(4)
(5)
式中:λeq为元件的等效故障率;μeq为元件的等效故障修复率;γeq为元件的等效故障修复时间。
2.1.2 带冷备用元件的可靠性模型
部分设备的修复过程较长,而更换过程时间相对较短,因此通常准备一个冷备用元件。当运行元件发生故障,将其退出运行,再安装备用元件,安装调试完毕,装置即可恢复正常运行。元件造价高,所以通常只准备一个备用元件,同时认为元件在处于备用状态时不会发生故障。当设备分别带一个冷备用元件,状态转移图如图3所示,这种情况下装置有5种运行状态。

图3 元件带一个冷备用的状态转移Fig.3 State transition diagram with one backup
根据图3的状态转移图,元件带1个备用的状态转移矩阵A如式(6)。求解式(6)得到图3中各个状态的稳态概率。进一步根据式(7—9)可求得元件等效可靠性参数。

(6)
(7)
(8)
(9)
2.2 UPFC可靠性模型
各个子系统按照上文所述方法建立两状态模型,各个子系统都对整个装置的正常运行有着重要的影响,任意子模块故障,系统都要退出运行状态,因此整个装置的可靠性评估模型可以看作是各个子系统的可靠性评估模型串联而成,得到整个装置的模型,状态空间图如图4所示。图中λeqi和μeqi分别是各个子系统的等效故障率和等效修复率。
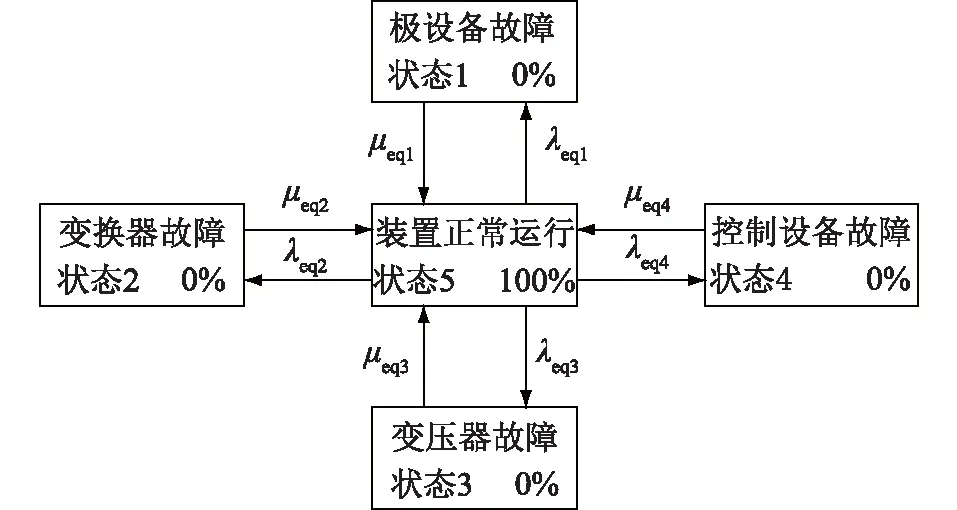
图4 UPFC状态空间转移Fig.4 UPFC state transition diagram
按照元件串联的关系,用串联等值公式可以求得整个UPFC的两状态模型和对应的可靠性指标。
(10)
(11)
(12)
式中:λUPFC是装置的等效故障率;γUPFC是每次故障平均修复时间;μUPFC是等效修复率。
2.3 含UPFC系统可靠性评估基本流程
含UPFC电网可靠性计算流程与常规电网可靠性计算总流程基本一致[14-15],主要包括以下4个步骤:
(1) 建立元件可靠性模型。UPFC可靠性建模方法如2.1-2.3节所述,最终可获得UPFC系统两状态的等效可靠性参数。系统中其它的发电机组、输电线路、变压器等元件采用常规两状态模型。
(2) 系统运行状态随机模拟抽样。文中采用蒙特卡洛模拟法对系统运行状态进行随机抽样[16-17]。
(3) 故障状态分析。对于出现元件故障的抽样状态,若出现支路潮流越限,则考虑通过发电机组功率调整或UPFC参数调整的方式消除支路潮流越限。文中采用的启发式调整过程如图5所示。

图5 支路越限调整流程Fig.5 Adjustment process of line power
(4) 可靠性指标计算。文中计算了切负荷频率、切负荷持续时间、电量不足期望值等18项可靠性指标。
3 实例分析
3.1 可靠性参数计算
发电机、线路、主变的可靠性参数基于中电联可靠性中心发布参数。发电机组非计划停运次数为0.34 次/(台·a),停运时间为24.44 h/(台·a)。线路、主变可靠性参数如表1所示。

表1 线路和主变可靠性参数Tab. 1 Line and transformer reliability data
UPFC装置中主要组合元件的可靠性原始参数参照柔性直流输电子系统可靠性参数[18],具体如表2所示。

表2 UPFC子系统可靠性参数Tab. 2 UPFC reliability data
按照前文所述子模块可靠性建模方法分别计算各个子模块的可靠性参数,再按状态合并方法得到各个子模块的两状态模型和对应的等效故障率、修复率。在元件是否有备用元件不同情况下的UPFC可靠性参数计算结果如表3所示。
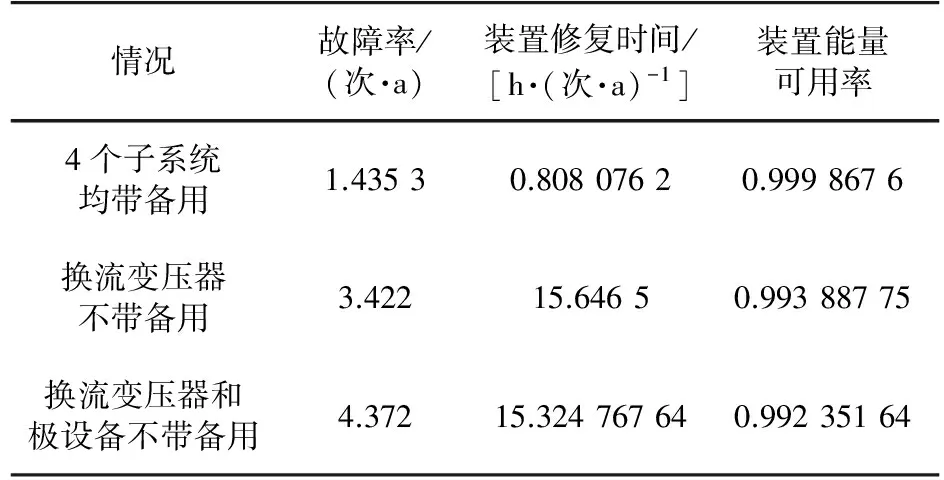
表3 UPFC可靠性参数计算结果
3.2 不同规划方案可靠性对比分析
为下列3种规划方案进行对比分析,验证UPFC对电网可靠性的影响。
(1) 新建线路方案。将220 kV华能南京—晓庄南侧线路单开环入220 kV码头,需建设电缆线路2×9 km,投资约9亿元。
(2) 线路倍容方案。将苏下关—苏晓庄和苏晓庄—苏中央线路约扩容,由原先750 A扩容到1500 A,需更换导线约30 km,但线路附近有高架路、居民小区、高层商住楼、京沪电气化铁路、加油站等设施,方案难以实施。
(3) 装设UPFC方案。本节计算选用UPFC可靠性参数:故障率=4.372 次/a,修复时间=15.324 8 h/(次·a)。3种情况下的可靠性指标计算结果如表4所示。

表4 可靠性指标计算结果Tab. 4 Calculation result of power system reliability
通过表4可知,新建线路方案、线路倍容方案可靠性均略高于线路倍容方案。这主要是由于新建线路方案、线路倍容方案从根本上提升了电网传输能力,因此可靠性略高。
然而,新建线路方案总投资远高于UPFC方案,同时其经济成本过高,且更换倍容导线方案由于政处原因,难以实施。因此,综合考虑工程经济性与可行性,南京西环网装设UPFC仍是合适方案。
3.3 UPFC安装位置不同可靠性影响分析
UPFC不同的安装位置也会对可靠性带来一定影响,此处重点分析了UPFC分别安装在铁北—晓庄双回、晓庄—中央与晓庄—下关线路、尧化—东阳双回双回不同位置下对电网可靠性的影响。

表5 UPFC不同安装位置下可靠性指标计算结果Tab. 5 Reliability calculation results under different installation positions of UPFC
通过表5可知,UPFC不同安装位置对可靠性影响较大,UPFC安装在铁北—双回线上可靠性比在晓庄—中央、晓庄—下关双线上可靠性下降50%;如果安装在尧化—东阳双线上,可靠性下降约500%。
4 结语
文中针对含UPFC南京西环电网系统可靠性进行研究,得到以下结论。
(1) 在UPFC可靠性建模中考虑有无备用元件的影响,能够使UPFC模型更贴近实际,提高分析结果的准确性;
(2) 在故障状态分析过程中,通过启发式方法计及UPFC参数调整消除线路潮流越限的作用,具有较高的计算效率;
(3) 在南京西环网系统,装设UPFC方案的可靠性水平略低于新建线路方案和线路倍容方案,但考虑经济性因素后,装设UPFC方案最为合适;
(4) UPFC不同安装位置对可靠性影响较大,在选择安装位置时需经详细比较确定。
[1] GYUGYI L.Unified power-flow control concept for flexible AC transmission systems[J]. IEEE Proceedings,1992, 139(4):323-331.
[2] GYUGYI L, SCHAUDER C D, WILLIAMS S L,et al.The unified power flow controller:a new approach to power transmission control[J]. IEEE Transactions on Power Delivery,1995,10(2):1085-1097.
[3] 窦 飞. 统一潮流控制器在南京220 kV西环网的应用研究 [D]. 华北电力大学,2015.
DOU Fei. Research on applications of UPFC in Nanjing 220 kV west loop[D]. North China Electric Power University,2015.
[4] 杨晓峰,林智钦,郑琼林,等. 模块组合多电平变换器的研究综述 [J]. 中国电机工程学报,2013,33(6):1-14.
YANG Xiaofeng,LIN Zhiqin,ZHENG Qionglin,et al. A review of modular multilevel converter[J]. Proceedings of the CSEE,2013,33(6):1-14.
[5] 蔡 晖, 祁万春, 黄俊辉,等. 统一潮流控制器在南京西环网的应用[J]. 电力建设, 2015, 36(8):73-78.
CAI Hui,QI Wanchun,HUANG Junhui,et al. Application of UPFC in Nanjing western power system[J]. Electric Power System,2015, 36(8):73-78.
[6] 林金娇, 李 鹏, 孔祥平,等. 南京西环网UPFC保护系统及配合策略[J]. 电力工程技术, 2015, 34(6):56-60.
LIN Jinjiao,LI Peng,KONG Xiangping,et al. The UPFC protection system configuration and action strategy in Nanjing western power grid[J]. Electric Power Engineering Technology, 2015, 34(6):56-60.
[7] 王 莹, 甄宏宁, 常宝立,等. UPFC在南京西环网中的应用需求分析[J]. 电力工程技术, 2016, 35(1):53-56.
WANG Ying, ZHEN Hongning, CHANG Baoli, et al. Research on the application of UPFC in Nanjing western grid[J]. Electric Power Engineering Technology, 2016, 35(1):53-56.
[8] 陈 刚, 李 鹏, 袁宇波. MMC-UPFC在南京西环网的应用及其谐波特性分析[J]. 电力系统自动化, 2016, 40(7):121-127.
CHEN Gang, LI Peng, YANG Yubo. Application of MMC-UPFC on Nanjing western grid and its harmonic analysis[J]. Automation of Electric Power System, 2016, 40(7):121-127.
[9] 祁万春, 杨 林, 宋鹏程,等. 南京西环网UPFC示范工程系统级控制策略研究[J]. 电网技术, 2016, 40(1):92-96.
QI Wanchun, YANG Lin, SONG Pengcheng, et al. UPFC system control strategy research in Nanjing western power grid[J].Power System Technology, 2016, 40(1):92-96.
[10] 李生虎,马燕如,董王朝. UPFC扩展状态空间模型和基于矩阵描述的可靠性灵敏度解析算法 [J]. 中国电机工程学报,2015,35(增刊):44-51.
LI Shenghu,MA Yanru,DONG Shengchao. Extended state space modeling and analytical reliability sensitivity algorithm based on matrix description for UPFC [J]. Proceedings of the CSEE,2015,35:44-51.
[11] 丁 明,汤海雁,吴红斌. 含UPFC的电力系统概率稳定分析 [J]. 电力自动化设备,2003,23(5):1-4.
DING Ming,TANG Haiyan,WU Hongbin. Probabilistic stability analysis of power system with UPFC[J]. Electric Power Automation Equipment,2003,23(5):1-4.
[12] 李 立,鲁宗相,邱阿瑞. 基于新负荷削减模型的UPFC优化配置 [J]. 电力系统自动化,2010,34(13):6-10.
LI Li,LU Zongxiang,QIU Arui. Optimal allocation of UPFC based on a new load curtailments model[J]. Automation of Electric Power System,2010,34(13):6-10.
[13] 王 勇, 韩学山, 丁 颖,等. 基于马尔科夫链的电力系统运行可靠性快速评估[J]. 电网技术, 2013, 37(2):405-410.
WANG Yong, HAN Xueshan, DING Ying, et al. Markov chain-based rapid assessment on operational reliability of power grid[J]. Power System Technology, 2013, 37(2):405-410.
[14] 张巍峰, 车延博, 刘阳升. 电力系统可靠性评估中的改进拉丁超立方抽样方法[J]. 电力系统自动化, 2015, 39(4):52-57.
ZHANG Weifeng, CHEN Yanbo, LIU Yangsheng. Improved Latin hypercube sampling method for reliability evaluation of power systems[J]. Automation of Electric Power System, 2015,39(4):52-57.
[15] 暴英凯, 王 越, 唐俊熙,等. 序贯蒙特卡洛方法在电力系统可靠性评估中的应用差异分析[J]. 电网技术, 2014, 38(5):1189-1195.
BAO Yingkai, WANG Yue, TANG Junxi, et al. Analysis on differences of applying sequential Monte Carlo methods in power grid reliability assessment[J]. Power System Technology, 2014, 38(5):1189-1195.
[16] 葛少云, 王浩鸣, 徐 栎. 基于蒙特卡洛模拟的分布式风光蓄发电系统可靠性评估[J]. 电网技术, 2012, 36(4):39-44.
GE Shaoyun,WANG Haoming, XU Li. Reliability of evaluation of distributed generating system including wind energy, solar energy and battery storage using Monte Carlo simulation[J]. Power System Technology, 2012, 36(4):39-44.
[17] 麻常辉, 梁 军, 杨永军,等. 基于蒙特卡罗模拟法的输电网灵活规划[J]. 电网技术, 2009, 33(4):99-102.
MA Changhui, LIANG Jun, YANG Yongjun, et al. Monte Carlo simulation based flexible planning of power transmission network[J]. Power System Technology, 2009, 33(4):99-102.
[18] 丁 明,毕 锐,王京景. 基于FD 法和模型组合的柔性直流输电可靠性评估[J]. 电力系统保护与控制, 2008, 36
(21):33-37.
DING Ming,BI Rui,WANG Jingjing. FD method and combined model for reliability assessment of HVDC flexible[J]. Power System Protection and Control, 2008, 36(21):33-37.
