一种求解二层单目标规划问题的基于KKT背离度量方程的粒子群优化算法
2018-02-07张钰张涛
张钰,张涛
(长江大学信息与数学学院,湖北 荆州 434023)
二层规划是一种具有递阶结构的系统优化问题。在二层规划模型中,一般可分为上、下2层,上层是一个含有下层最优决策变量(或最优目标函数值)的复合最优化问题,下层则是一个以上层决策变量为参数的参数规划[1~3]。二层规划的嵌套结构使得该模型的求解具有一定的复杂性,其复杂性表现在上层目标函数决定于下层规划问题的解函数,通常这个解函数非凸且不可微;二层规划约束的嵌套特性使其可行域一般不再具备凸性和闭性,并且在有包含下层决策变量的上层约束时还可能不连通,甚至是空集。
目前,求解二层规划问题的传统算法可以分为4类:Karus-Kuhn-Tucker方法[4~7]、分支定界法[8]、罚函数法[9~12]以及下降法[13,14],这些传统算法均要求目标函数具有可微性和连续性。然而,二层规划问题的目标函数通常不具备上述属性且非凸。粒子群优化算法[15]作为近来提出的一种智能算法,其算法特点与二层规划问题的结构特征具有优良的匹配性:该算法对模型结构以及目标函数和约束函数的性态要求更为宽松,且该算法以种群为操作单元且实数编码,可以与二层规划问题的下层问题的多解特征建立映射关系。因此,利用粒子群算法求解二层规划问题是一条有效途径。2006年,Li等[16]提出了求解二层规划问题的分层粒子群算法;2009年,Kuo与Huang[17]提出了求解线性二层规划问题的粒子群算法;2011年,Gao等[18]利用粒子群算法求解了供应链中的二层规划模型;随后,Zhang等[19]利用粒子群优化技术求解了电力市场中的竞争性招标策略的二层规划模型;2013年,Jiang等[20]提出了基于CHKS光滑方程的粒子群算法求解非线性二层规划问题。上述二层规划模型的决策变量维数较低且模型相对较为简单。对于维数较高且函数性态(可微性、连续性及多模态性)较为复杂的二层规划模型,利用上述算法进行求解时,将会花费巨大的计算代价且收敛性得不到保障。针对复杂的二层规划模型,利用粒子群算法求解的核心是确保下层规划问题的最优解的精确性,如果所求下层问题的最优解具有非精确性或欺骗性,则整个问题求解将会花费巨大计算代价甚至求解失败。为此,笔者基于单目标规划问题的KKT条件,引入KKT背离度量方程,利用该度量方程控制下层问题的最优解精度,然后以下层问题最优解精度控制值为终止条件,设计求解二层规划问题的粒子群算法。
1 模型与基本概念
假设x∈Rn1,y∈Rn2,F,f:Rn1×Rn2→R,G,g:Rn1×Rn2→R,乐观二层单目标规划可表述为:
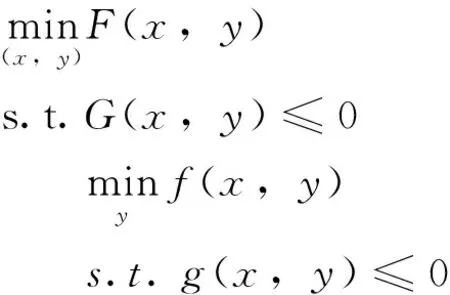
(1)
式中,x∈Rn1和y∈Rn2分别为上层决策变量和下层决策变量;F(x,y)和f(x,y)分别表示上层目标函数和下层目标函数;G(x,y)和g(x,y)分别表示上层约束函数和下层约束函数。
记:
约束域S={(x,y)|G(x,y)≤0,g(x,y)≤0}
对于给定x∈Rn1,下层问题的可行域S(x)={y|g(x,y)≤0}
约束域S在上层问题决策空间的投影S(X)={x|∃y,G(x,y)≤0,g(x,y)≤0}
对于x∈S(X),下层问题的合理反应集P(x)={y|y∈arg min[f(x,y):y∈S(x)]}
二层单目标规划问题的诱导域IR={(x,y)|(x,y)∈S,y∈P(x)}
定义1 如果点(x,y)∈IR,则称点(x,y)为问题(1)的可行点。
定义3 如果(xo,yo)成为问题(1)的乐观最优解, 则 (xo,yo)满足如下方程:
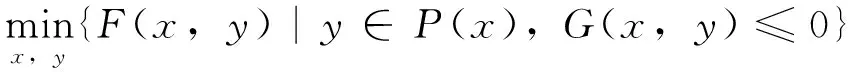
2 算法设计
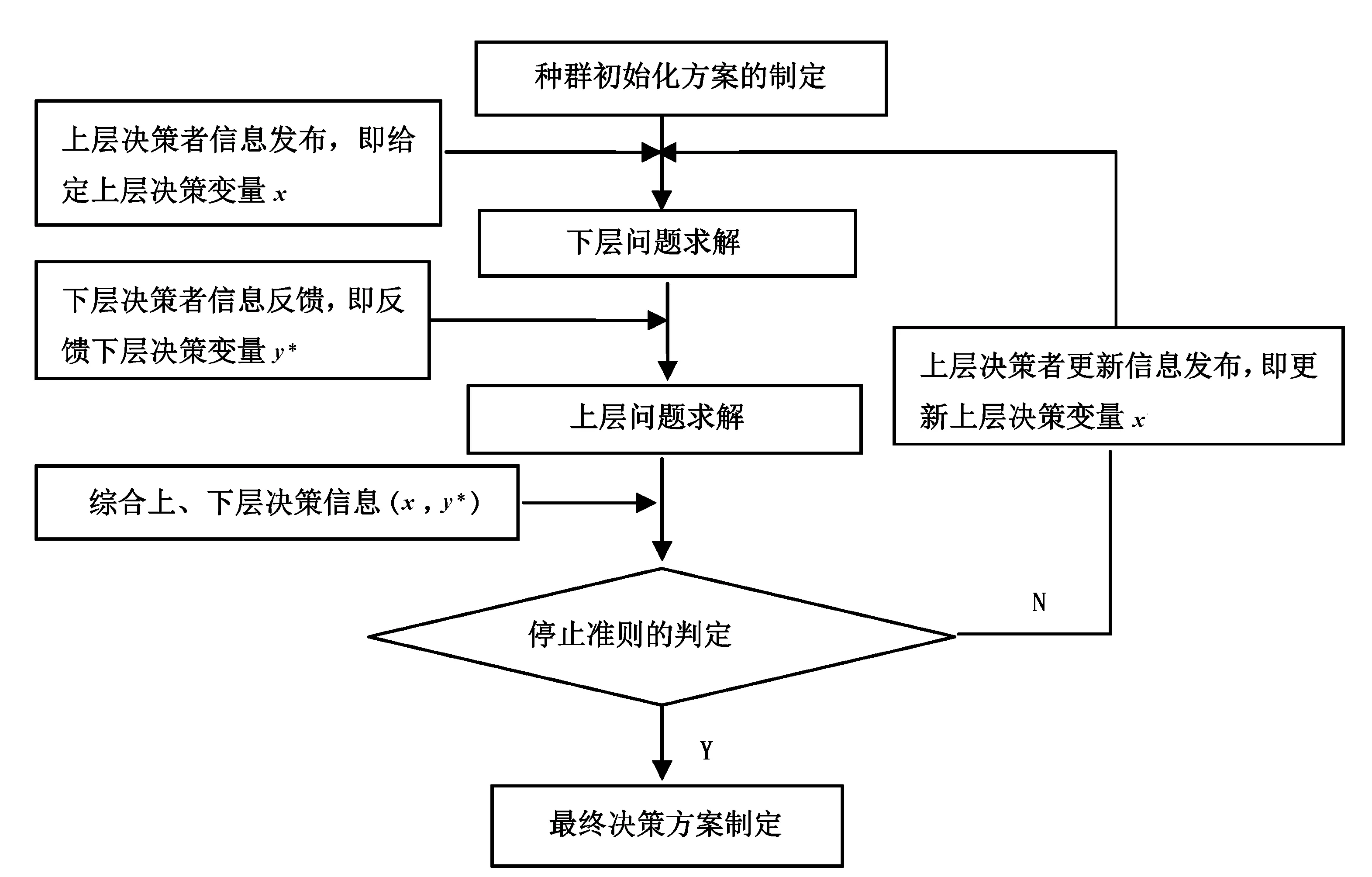
利用粒子群优化算法求解二层规划问题的基本工作流程如图1所示:给定上层决策变量,执行下层优化问题;然后将下层问题的近似最优解作为最优响应反馈给上层,从而得到整个问题的近似最优解;通过预设迭代次数,使整个问题的近似最优解任意精度逼近精确解。具体步骤如下:
Step1 初始化上层种群Pu,种群规模为Nu,初始化上层循环变量tu=0。
Step2 对于上层决策变量xi(i=1,2,…,N), 初始化下层种群Pl,种群规模为Nl,初始化下层迭代次数tl=0。
Step3 执行下层优化问题。更新下层粒子的速度和位置:
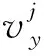
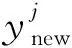
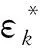
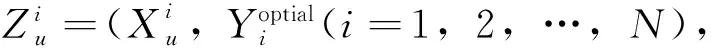
Step6 上层问题的终止条件检查,如果α(tu)≥α-predefined,转Step7,否则输出上层问题的最优解。
Step7 按如下方程更新上层决策变量:
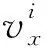
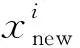
Step8 对于更新的上层决策变量,转Step2。
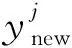
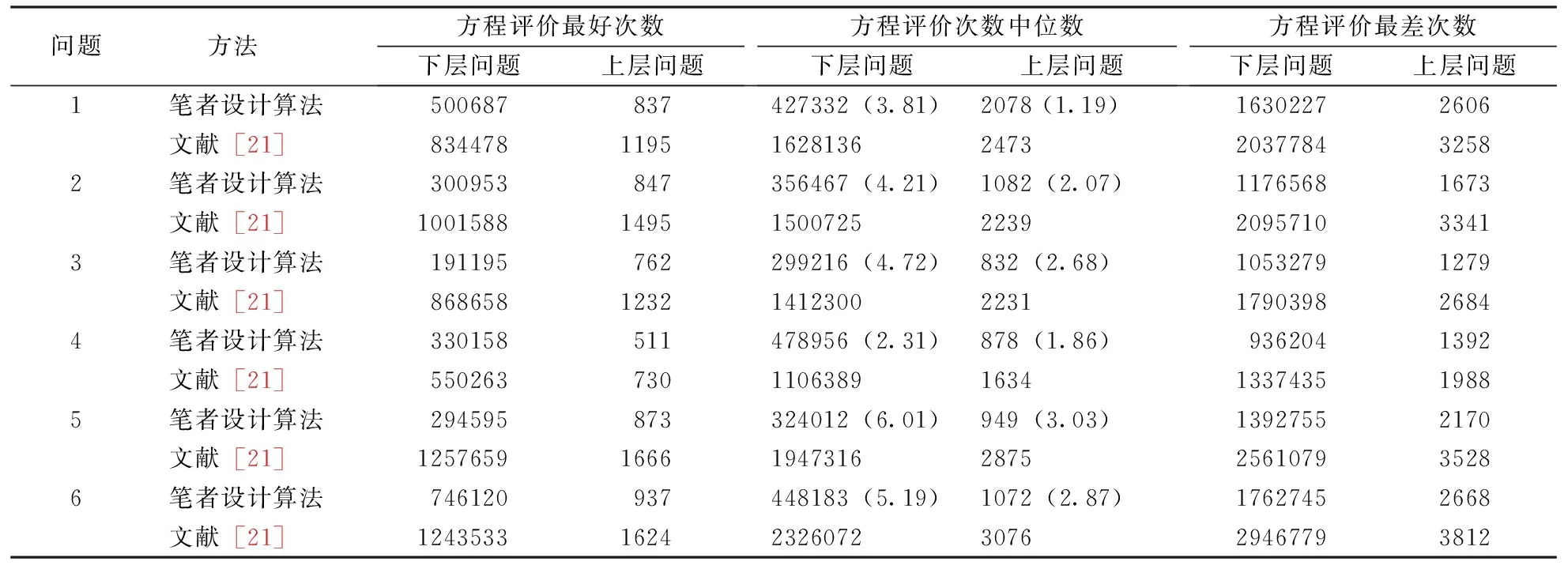
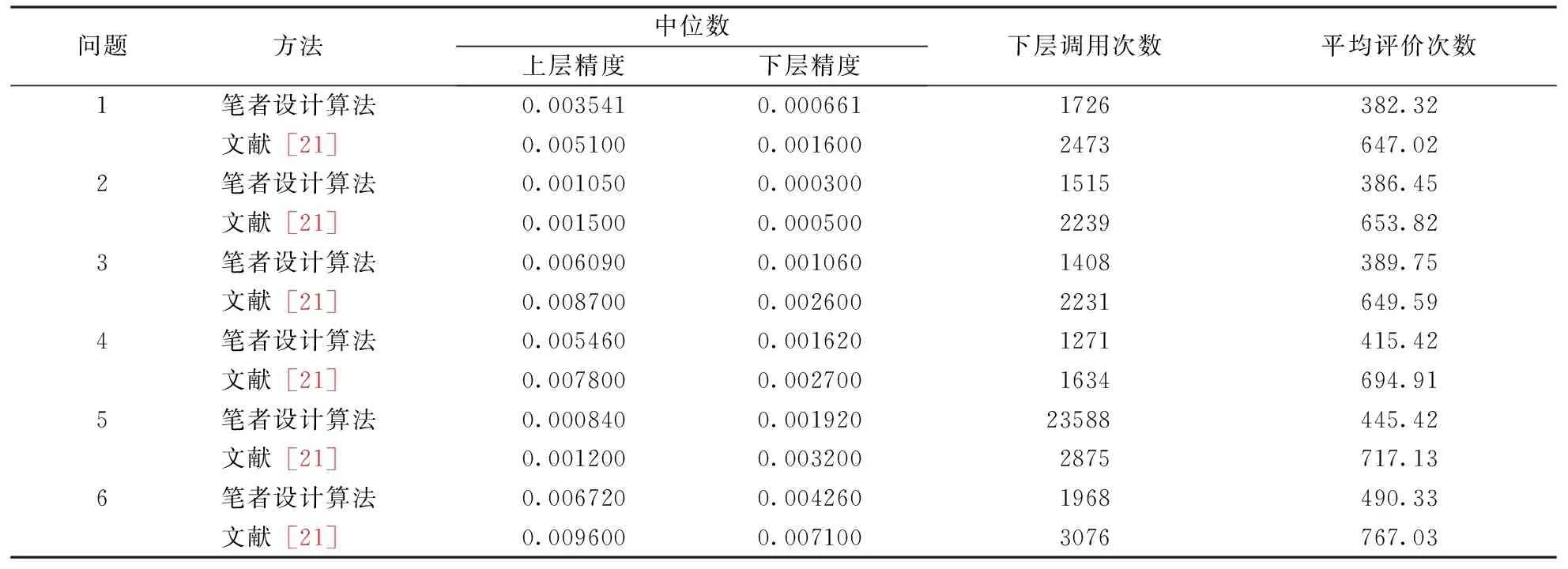
如果yj 如果pbestj(y) 如果yj与pbestj(y)相等,则从两者之中随机挑选一个作为新的pbestj(y)。 Step7中的pbestj(y)按同样的方式选取。 在Step4中,下层规划问题基于KKT背离度量方程的终止条件为: (2) (3) (4) 图1 二层规划问题的粒子群算法的基本工作流程 粒子群优化算法的相关参数设置如下:r1,r2∈random(0,1),惯性权重w=0.7298,社会系数和认知系数c1=c2=1.49618,上层问题和下层问题的粒子规模Nu=Nl=50。下层问题的终止精度为1×10-4,计算机运行条件CPU:AMDPhenon(tm)ⅡX6 1055T2.80GHz;RAM:3.25GB,利用C#编程进行求解。 以下分别为仿真试验算例。 问题1: 问题2: 问题3: 问题4: 问题5: 问题6: 其中,问题1~问题5参数设置p=5,q=5,r=2;问题6的参数设置p=5,q=3,r=2,s=2。 将上述算例执行11次并与参考文献[21]中的结果做比较,表1给出了上层问题和下层问题的方程评价次数的比较结果,表2给出了上层问题和下层问题精度的比较结果。 表1 上层问题和下层问题方程评价次数的比较结果 表2 上层问题和下层问题最优解的精度比较结果 表1中,第5列与第6列分别表示下层问题和上层问题的方程评价次数的中位数。括号中的数值表示文献[21]中的算法所需方程评价次数的中位数与笔者设计算法所需方程评价次数中位数的比率。从比较结果来看,2种方法都能成功求解所有问题,但从上层问题方程评价次数的中位数来看,文献[21]中的算法所需次数是笔者设计算法所需次数的1.19~3.03倍,从下层问题方程评价次数的中位数来看,文献[21]中的算法所需的次数是笔者设计算法所需次数的2.31~6.01倍。 从表2中可以看出,在获得问题的几乎相同的精度解时,文献[21]中的方法所执行的下层优化问题的次数约为笔者设计算法的1.5倍,且每执行一次下层优化问题文献[21]中的方法所需的方程评价次数约为笔者设计算法所需方程评价次数的1.6倍。 提出了一种基于KKT背离度量方程的粒子群算法用于求解二层规划问题的乐观解,用6组模型进行仿真试验并与经典文献中的计算结果做了比较,结果表明KKT背离度量方程能够有效的保证下层问题最优解的真实性,从而较大幅度的减少了计算量并在一定程度上改善了算法的收敛速度。在未来的研究中,将进一步考虑在维数迅速膨胀的情况下如何设计该问题的并行粒子群算法。 [1]Bard J F, Falk J E. An explicit solution to the multilevel programming problem [J]. Computers and Operations Research, 1982, 9(1): 77~100. [2]Demple S. Foundation of Bilevel Programming [M]. London: Kluwer Academic, 2002. [3]藤春贤,李智慧. 二层规划理论与应用 [M]. 北京:科学出版社,2002. [4] Bard J.An algorithm for solving the general bilevel programming problem[J]. Mathematics of Operations Research, 1983,8:260~272. [5] Edmunds T, Bard J.Algorithm for nonlinear bilevel mathematical programs[J]. IEEE Transactions on Systems,1991,21:83~89. [6] Amouzegar M.A global optimization method for nonlinear bilevel programming problems[J]. IEEE Transactions on Systems, 1999,29:771~777. [7] Etoa J.Solving quadratic convex bilevel programming problems using a smoothing method[J]. Applied Mathematics and Computation,2011,217:6680~6690. [8] Bard J, Falk J.An explicit solution to the multi-level programming problem[J]. Computers & Operations Research,1982,9:77~100. [9] Ishizuka Y, Aiyoshi E.A new computational method for Stackelberg and min-max problems by use of a penalty method[J]. IEEE Transactions on Automatic Control,1981,26:460~466. [10] Aiyoshi E, Shimuzu K.A solution method for the static constrained Stackelberg problem via penalty method[J]. IEEE Transactions on Automatic Control, 1984,29:1112~1114. [11] Ishizuka Y, Aiyoshi E.Double penalty method for bilevel optimization problems[J]. Annals of Operations Research,1992,34:73~88. [12] Lv Y, Hu T, Wang G,et al. A penalty function method based on Kuhn-Tucker condition for solving linear bilevel programming[J].Applied Mathematics and Computation,2007,188:808~813. [13] Savard G, Gauvin J.The steepest descent direction for the nonlinear bilevel programming problem[J].Operations Research Letters,1994,15:265~272. [14] Falk J, Liu J.On bilevel programming, Part I: general nonlinear cases[J].Mathematical Programming,1995,70:47~72. [15]Kennedy J, Eberhart R C. Particle swarm optimization[A]. Proceedings of IEEE International Conference on Neural Networks [C]. 1995:1942~1948. [16] Li X, Tian P, Min X.Hierarchical Particle Swarm Optimization for Solving Bilevel Programming Problems[A]. Lecture Notes in Computer Science[C]. 2006:1169~1178. [17] Kuo R, Huang C.Application of particle swarm optimization algorithm for solving bilevel linear programming problem[J].Computer and Mathematics with Application,2009,58:678~685. [18] Gao Y, Zhang G, Lu J, et al.Particle swarm optimization for bi-level pricing problems in supply chains[J].Journal of Global Optimization,2011, 51:245~254. [19] Zhang G, Zhang G, Gao Y, et al.Competitive strategic bidding optimization in electricity markets using bi-level programming and swarm technique[J].IEEE Transactions on Industrial Electronics,2011,58: 2138~2146. [20] Jiang Y, Li X.Application of particle swarm optimization based on CHKS smoothing function for solving nonlinear bilevel programming problem[J].Applied Mathematics and Computation,2013,129:4332~4339. [21] Sinha A, Malo P, Deb K. Efficient evolutionary algorithm for single-objective bilevel optimization[J].Neural and Evolutionary Computing, 2013,18(3): 403~449.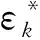
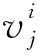
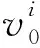
3 数值仿真与结果分析
4 结语
