一种适用于惯性-地磁组合的自适应卡尔曼算法

戎海龙，彭翠云

1.常州大学 城市轨道交通学院，江苏 常州 213164

2.常州大学 信息科学与工程学院，江苏 常州 213164

1 引言

惯性-地磁组合一般由三轴MEMS（微机电系统）陀螺仪、三轴MEMS加速度计和三轴MEMS地磁传感器组成，然后通过多传感器信息融合技术获得运动体姿态，在人体运动分析等领域应用很广泛。这种组合可以看做是两种姿态测量方法的重新组合。众所周知，单独利用三轴陀螺仪也可以实现姿态测量（基于多加速度计组合的所谓的无陀螺捷联惯导系统也可以归为此类），这种姿态测量方法的短时测量精度很高，相应的姿态解算算法包括方向余弦算法、欧拉角法、四元数微分算法、等效矢量算法等，然而这些算法全部建立在数值积分的基础上，因而如果陀螺仪为MEMS陀螺仪，则其自身所具有的幅值较大的随机噪声及从根本上无法完全消除的转动不可交换性误差很容易使解算结果快速发散，因而这种方法并不适合长时间的姿态测量。利用三轴加速度计和三轴地磁传感器也可以获得运动体姿态，这种方法的静态精度很高，相应的姿态解算算法包括TRIAD算法、QUEST算法、FORM算法、ESOQ、ESOQ2算法、q-算法、Euler-q算法等，然而加速度计不可能只测量运动体重力加速度，况且人体运动有一个不同于机械运动（包括飞行器）的特点，即运动的线加速度复杂多变，无规律可循，采用建模的方法抑制线加速度对算法本身的影响并不现实，因而即使加速度计精度再高，上述算法的动态精度仍然很差。惯性-地磁组合的目的是将上述两种方法重新进行组合，进而获得更好的静动态精度，采用的姿态解算算法包括状态方程非线性[1]或观测方程非线性[2-5]的扩展卡尔曼算法、互补滤波算法[6-8]、梯度下降算法[9]，以及经作者[10]实验研究发现也适用的REQUEST 算法[11]、Optimal-REQUEST 算法[12]、自适应Optimal-REQUEST算法[13]、filter-REQUEST算法[14]等，这些算法均为迭代算法，基本思想类似。状态方程非线性的卡尔曼算法的观测矩阵为单位阵，并假设载体角速度为一阶马尔科夫过程，因此对加速度计和地磁传感器组合的依赖较大，这使得该算法的静态结果较高且不发散，然而动态精度欠佳；观测方程非线性的扩展卡尔曼算法由于状态噪声取的过小（按MEMS陀螺仪实际噪声间接得出）导致卡尔曼增益很小，进而使得其对陀螺仪的依赖较大，因而其静态结果存在缓慢发散现象，但是其动态精度较高；互补滤波算法和梯度下降算法可以分别通过调整其截止频率和相关的权值实现对陀螺仪或者加速度计与地磁传感器组合的依赖程度，但调整的依据没有提及，如果调整不合适，则亦或动态精度较低，亦或静态精度较差；REQUEST算法家族随着其记忆因子的逐步衰减，对加速度计和地磁传感器组合的依赖程度越来越小，因此一段时间之后其动态精度比观测方程非线性的扩展卡尔曼算法精度更高，然而由于过分依赖陀螺仪，使得其发散现象比观测方程非线性的扩展卡尔曼算法更严重。如果能够根据运动体运动情况对观测噪声或者过程噪声进行实时估计，也就是采用自适应卡尔曼算法[15]显然是比较合适的，然而自适应卡尔曼算法适用的前提是观测噪声为方差可变的白噪声，因此该算法目前只在组合导航系统中GPS观测噪声实时估计上获得应用。已有学者采用下式作为观测噪声调整依据：其中ax(k)、ay(k)、az(k)分别为由k时刻加速度计测得的三轴向加速度分量（包括线加速度和重力加速度分量），而后或者采用门技术[4]调整观测噪声方差或者直接将上式作为观测噪声并对其方差进行实时估计[3，5]，这些方法尽管简单有效，但是有四个问题：（1）很明显，上式并不能看做噪声，它甚至根本不是一个平稳过程；（2）加速度计存在输出零偏和随机游走，这会对上式造成误差；（3）用上式表示运动体线加速度大小并不准确，εo=0时，上式在三维坐标系下可表示为一个球，球表面上的任何点均满足该式，这意味着满足该式并不代表运动体处于静止状态；（4）运动体线加速度是无界的，如果过大，则有可能导致算法过于依赖陀螺仪而发散。本文仍然将观测方程非线性的扩展卡尔曼算法作为姿态解算算法，然而将给出一种新的观测噪声，这种观测噪声的方差在运动体运动时会增大，进而加大对陀螺仪的依赖，这将构成一种真正意义上的自适应扩展卡尔曼算法，实验表明这种算法是比较有效的。

2 基于观测噪声实时估计的自适应EKF算法

卡尔曼算法的k+1时刻的验后估计为：

Fk+1为k+1时刻的观测阵（或者线性化后的观测阵）；Rk+1为观测噪声；为k+1时刻的先验估计的误差协方差阵：

Qk为过程噪声；Pk为k时刻的验后估计的误差协方差阵。

REQUEST算法的迭代方程为：

其中bi和ri为k时刻由三轴加速度计（三轴地磁传感器）得到的载体坐标系表示的重力矢量（地磁场矢量）观测值以及该矢量在参考坐标系下的表示值；ρk为记忆因子，取值在0至1之间，用于逐步舍弃最初的历史测量信息，避免逐步累积的测量误差严重污染K矩阵。k+1时刻的姿态四元数qk+1为与矩阵Kk+1/k+1的最大特征值相对应的归一化的特征向量。

由式（1）和式（4）知，k+1时刻的姿态估计结果由两部分组成，第一项为姿态预测，由三轴陀螺仪得到，第二项为姿态修正（姿态修正增益分别为Kk+1和1 mk+1），由三轴加速度计和三轴地磁传感器得到。由式（1）可知，卡尔曼增益阵Kk+1中的元素值越小，则姿态修正量越小，估计结果越依赖于陀螺仪，反之则越依赖于加速度计和地磁传感器组合。状态方程非线性的卡尔曼算法由于其观测阵为单位阵，其卡尔曼增益阵中的元素数量级恒定维持在101左右，这就表明状态方程非线性的卡尔曼算法侧重于依赖加速度计和地磁传感器组合。观测方程非线性的卡尔曼算法的过程噪声协方差阵中的元素与采样时间的平方成正比，而通常惯性-地磁组合的采样时间在几十毫秒，因此，由式（2）和（3）不难发现卡尔曼增益被严重衰减，这表明观测方程非线性的卡尔曼算法更倾向于依赖陀螺仪信息。由式（4）可知，随着时间的增长，1 mk+1逐渐衰减至0，mkmk+1逐渐接近1，这就表明REQUEST算法对陀螺仪的依赖程度更甚于观测方程为非线性的卡尔曼算法。以上分析表明状态方程非线性的卡尔曼算法的静态精度比观测方程为非线性的卡尔曼算法和REQUEST算法要高，而动态精度要差。

为了获得更好的静动态性能，一个自然的想法是观测噪声的方差与运动体线加速度的大小成正比，进而通过观测噪声方差间接调整姿态修正增益，使得在运动体运动时加大对陀螺仪的依赖。由于状态方程非线性的卡尔曼算法观测矩阵为单位阵，由式（2）不难看出该算法的增益阵几乎不受过程噪声和测量噪声的影响，所以通过干预过程噪声或者测量噪声的办法来干预姿态修正增益几乎没有效果。而由式（4）可以看出，姿态修正增益1 mk+1随时间逐渐衰减，对其进行调整的结果只能是减缓其衰减的速度，因此调整REQUEST算法的姿态修正增益是没有意义的。基于上述原因，本文采取实时调整观测方程非线性的卡尔曼算法的观测噪声的方法来达到此目的。

假设x=vg×vm，其中“×”表示两矢量的向量积。对x求导得到：

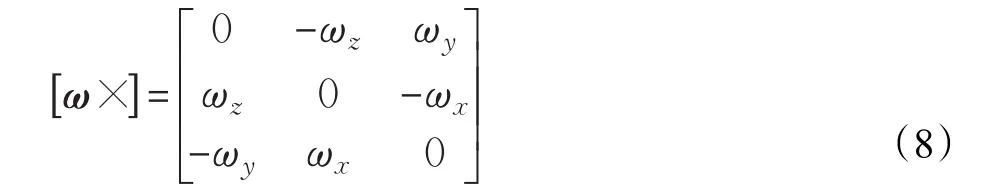
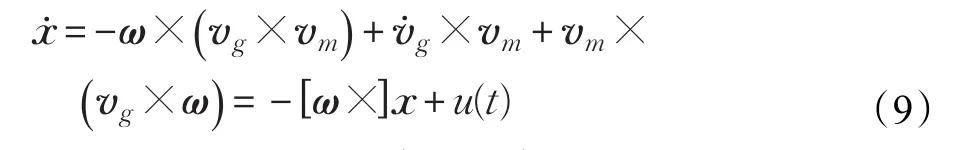
取测量方程

其中C为单位阵。

将式（9）与式（10）组合在一起，并考虑过程噪声及观测噪声后形成如下方程组：

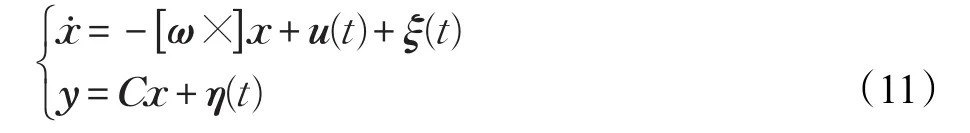
之所以考虑过程噪声及观测噪声，是由于观测矢量vg、vm和ω本身存在测量噪声，而且[ ]ω×、u(t)只能采用这些观测矢量计算。将式（11）离散化，得到：

其中，k表示具体的采样时刻。

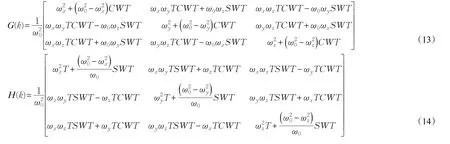
ξ(t)和η(t)可以由式（15）得到：

由式（12）及式（15）可以发现：（1）过程噪声和观测噪声并不为白噪声；（2）两种噪声之间是相关的；（3）两种噪声的方差阵及两者之间的协方差阵在不断变化。为简化计算起见，可以否定上述三条结论，针对式（15）的大量仿真计算也说明了这一点。可以定义

其中Q、R为常量，可以利用式（15）估算，然后根据卡尔曼滤波效果再做调整。卡尔曼滤波公式限于篇幅略去。

待x(k)估计出后，可利用式（17）计算估计残差：

其中，ρ＞0残差调整因子。值得指出的是，Allan方差分析表明，加速度计等惯性器件的输出零偏和随机游走属于低频成分，卡尔曼滤波器属于低通滤波器，其本身又是无偏估计，所以加速度计的输出零偏和随机游走会直接通过卡尔曼滤波器而叠加到其输出中，这就使得利用

图2 静态测试条件下MTi姿态输出结果

式（17）计算出的估计残差中不会包含任何有关加速度计的输出零偏和随机游走的成分。上述结论表明加速度计的输出零偏和随机游走并不影响本文算法。

估计残差的方差可利用滑窗估计的方法（式（18））实时计算

其中，n为截取的滑窗长度。

观测方程非线性的卡尔曼算法的观测噪声的协方差可按照下式实时进行调整：

3 实验结果

3.1 实验设置

如图1所示。实验时将新近购得的两种惯性-地磁组合MTi和ADIS16480通过扎带固定于滑台上，滑台可以用手驱动在滑轨上做往复直线运动。MTi的基本噪声参数为陀螺仪0.34°/s、加速度计0.008 m/s2、地磁传感器0.1 μT，ADIS16480的基本噪声参数则分别为0.16 °/s、0.014 7 m/s2及0.045 μT。这两种惯性地磁组合的采样率分别为256 Hz和307.5 Hz。本文算法以ADIS16480输出的原始传感器数据解算姿态。姿态用欧拉角表示，并且为了清晰展示，姿态解算结果已经除去了其均值量。Q=0.01，R=0.1，ρ =100，n=30[3]。

图1 实验设置

3.2 静态测试

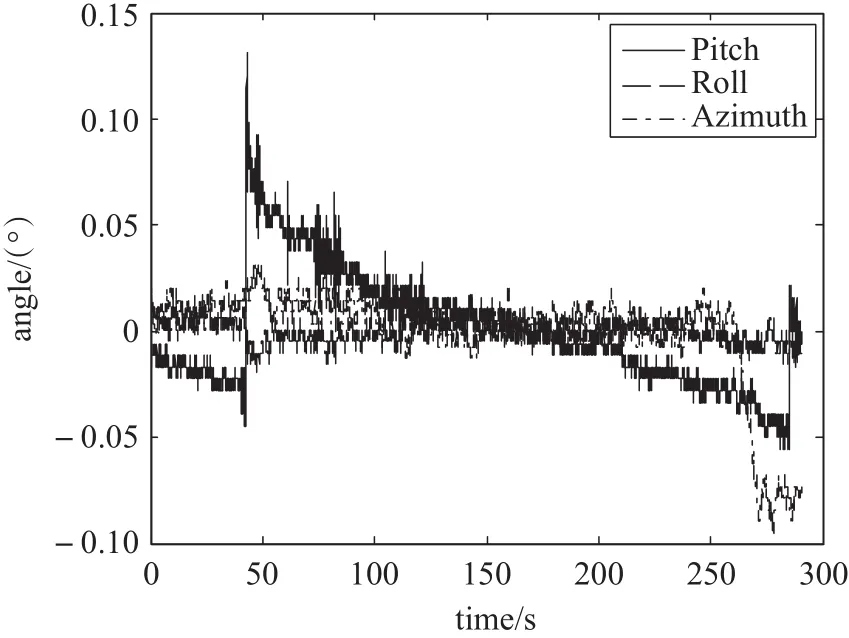
图3 静态测试条件下ADIS16480姿态输出结果

将两种惯性-地磁组合在滑台上静止一段时间，以测试静态精度。图2和图3分别为MTi和ADIS16480内置的卡尔曼算法的姿态解算结果，图4为本文姿态解算结果，图5为REQUEST算法的姿态解算结果，其中REQUEST算法的记忆因子取为0.9。

3.3 动态测试

在手带动下使滑台在滑轨上做一段时间的往复直线运动。图6～8为ADIS16480输出的传感器原始数据，图9～12为姿态解算结果，图13为估计残差及其方差估计结果。

3.4 结果分析

对比图2～5可以发现，在静止情况下ADIS16480内置卡尔曼算法和本文算法的姿态解算精度相当且较高，均倾向于依赖加速度计和地磁传感器信息，而MTi内置的卡尔曼算法的姿态解算结果出现了发散现象，这说明MTi更倾向于依赖陀螺仪信息，REQUEST算法对陀螺仪信息依赖更严重，使得其姿态解算结果发散现象更严重，这也是为何REQUEST算法能够应用于广泛使用光纤、激光或者静电陀螺的航空航天领域而无法在普遍使用MEMS陀螺的民用领域获得推广的根本原因。

图4 静态测试条件下本文姿态解算结果

图5 静态测试条件下REQUEST算法姿态结算结果

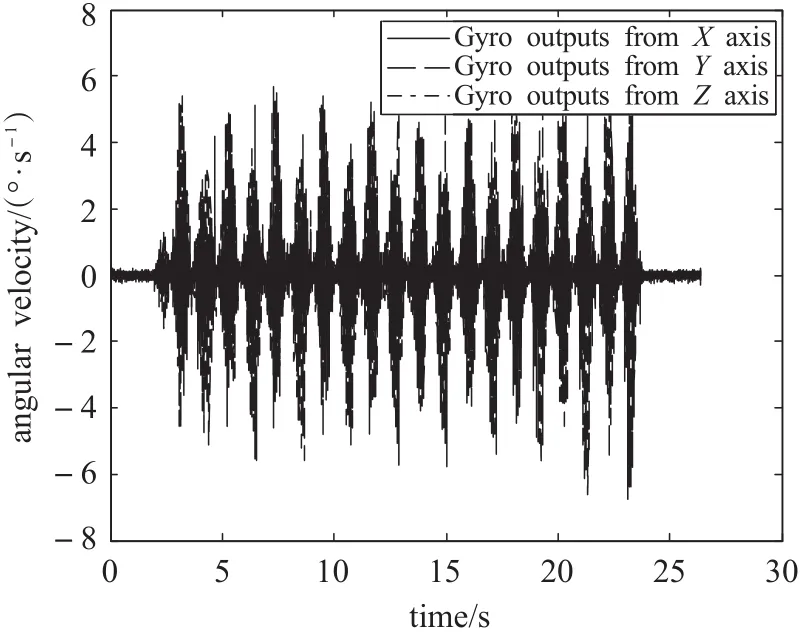
图6 动态测试条件下ADIS16480陀螺仪输出结果

图7 动态测试条件下ADIS16480加速度计输出结果

图8 动态测试条件下ADIS16480地磁传感器输出结果

图9 动态测试条件下MTi姿态输出结果

图10 动态测试条件下ADIS16480姿态输出结果

图11 本文姿态解算结果

图12 动态测试条件下REQUEST算法姿态解算结果

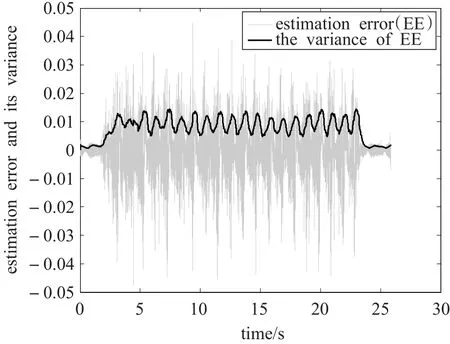
图13 估计残差及其方差

由图6～8所示，如果在某段时间内（图中的1.85～23.9 s）使滑台做直线往复运动而保持姿态不变，那么各种算法的姿态解算结果如图9～12所示，很明显，由于姿态保持不变，那么如果某种算法姿态解算结果出现变化，此变化量即为误差，ADIS16480仍然倾向于依赖加速度计和地磁传感器信息，这使得其姿态解算结果出现大幅摆动，俯仰角摆幅近似在±10°以上，而MTi倾向于依赖陀螺仪信息，所以其姿态解算结果的摆动较小，俯仰角摆幅近似在±1°左右，REQUEST算法给出的姿态解算结果也出现摆动，但是摆动逐步衰减，运动初始时刻俯仰角摆幅近似为±4°，而运动终止时近似在±0.75°左右，REQUEST算法对陀螺仪的依赖程度是一个逐步增大的过程，因此，如果在使滑台运动之前使其处于静止状态更长一段时间，那么其动态精度会更好一些。由图13可以看到估计残差在滑台运动时会增大，本文利用这一特点实现的自适应扩展卡尔曼算法的姿态解算结果如图11所示，很明显其俯仰角摆幅只有±0.2°左右，是上述所有算法中摆幅最小的，这说明在滑台运动时，通过自适应调整观测噪声，使算法在此时加大对陀螺仪的依赖，从而减少动态误差，但同时也应看到，由于对陀螺仪误差加大，算法出现缓慢发散现象。

4 结论

本文在观测方程非线性卡尔曼算法的基础上给出了一种新的自适应扩展卡尔曼算法，该方法利用线性卡尔曼算法实时估计‖，并将估计残差作为用于姿态解算的扩展卡尔曼算法的观测噪声，原因在于该估计残差在运动体静止和运动时方差并不相同，这样就使得该算法可以兼具更好的静动态性能。由于采用线性卡尔曼算法，本文提出的方法并不会大幅度提高扩展卡尔曼算法的运行时间。

未来将在以下两个方面继续开展研究：（1）事实上，估计残差虽然为零均值且平稳，但并不为白噪声，这将使得本文提出的自适应扩展卡尔曼算法并不是最优的，因此需要进一步做白化处理；（2）残差调整因子ρ的取值是根据实验调整的，并没有根据某种准则做最优选取。

[1]Yun X P，Bachmann E R.Design，implementation，and experimental results of a quaternion-based Kalman filter forhuman body motion tracking[J].IEEE Transactions on Robotics，2006，22（6）：1216-1227.

[2]Sabatelli S，Galgani M，Fanucci L，et al.A double stage Kalman filter for sensor fusion and orientation tracking in 9D IMU[C]//Proceedings of IEEE Symposium on Sensors Applications，Brescia，Italy，2012：1-5.

[3]Sessa S，Zecca M，Lin Z H，et al.A methodology for the performance evaluation of inertial measurement units[J].Journal of Intelligent&Robotic System，2013，71（2）：143-157.

[4]Sabatini A M.Kalman-filter-based orientation determina-tion using inertial/magnetic sensors：Observability analysis and performance evaluation[J].Sensors，2011，11（10）：9182-9206

[5]Ren H L，Kazanzides P.Investigation of attitude tracking using an integrated inertial and magnetic navigation system for hand-held surgical instruments[J].IEEE/ASME Transactions on Mechatronics，2012，17（2）：210-217.

[6]Gallagher A，Matsuoka Y，Ang W T.An efficient realtime human posture tracking algorithm using low-cost inertial and magnetic sensors[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems，Sendai，Japan，2004：2967-2972.

[7]Harms H，Amft O，Winkler R，et al.ETHOS：Miniature orientation sensor for wearable human motion analysis[C]//Proceedings of IEEE Conference on Sensors，Kona，USA，2010：1037-1042.

[8]Campolo D，Taffoni F，Formica D.Inertial-magnetic sensors for assessing spatial cognition in infants[J].IEEE Transactions on Biomedical Engineering，2011，58（5）：1499-1503.

[9]Madgwick S O H，Harrison A J L，Vaidyanathan R.Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//Proceedings of IEEE International Conference on Rehabilitation Robotics，Zurich，Switzerland，2011：1-7.

[10]戎海龙，戴先中，刘信宇.烹饪过程中锅具运动姿态测量方法[J].中国惯性技术学报，2009，17（4）：419-423.

[11]Bar-itzhack I Y.Request：A recursive QUEST algorithm for sequential attitude determination[J].Journal of Guidance，Control and Dynamics，1996，19（5）：1034-1038.

[12]Choukroun D，Bar-itzhack I Y，Oshman Y.Optimal-REQUEST algorithm for attitude determination[J].Journal of Guidance，Control and Dynamics，2004，27（3）：418-425.

[13]Choukroun D.Adaptive optimal-request algorithm for attitude determination[C]//Proceedings of AIAA Guidance，Navigation，and Control Conference，Hilton Head，USA，2007：4624-4647.

[14]Shuster M D.Filter QUEST or REQUEST[J].Journal of Guidance，Control and Dynamics，2009，32（2）：643-645.

[15]卞鸿巍，金志华，王俊璞，等.组合导航系统新息自适应卡尔曼滤波算法[J].上海交通大学学报，2006，40（6）：1000-1003.