船舶动力定位控制系统的非线性观测器设计
2018-02-07陈勇嘉杨宣访王永建
陈勇嘉 杨宣访 王永建
(海军工程大学电气工程学院 武汉 430033)
1 引言
动力定位(DP)[1]是指船舶不借助锚泊,仅通过自身安装的推进器来抵抗风、浪、流等环境干扰的影响,实现其在海面上固定位置或预期航迹的保持。环境干扰对船舶的影响可以分为由风、流和二阶波浪导致的低频运动,和由一阶波浪导致的高频运动。其中高频运动只引起船舶的周期性振荡而不会造成船体大范围偏离平衡位置,为避免能量浪费和推进器磨损,而尽量不响应一阶波浪、噪声等高频振荡干扰信号的作用,这就需要根据传感器测量的信息和船舶动力定位控制的数学模型估计出船舶的低频运动状态,因此状态估计方法在动力定位控制系统的设计中具有非常重要地位,是动力定位控制系统的关键技术之一[2]。
DP系统从20世纪60年代开始应用在海洋船舶上,采用了陷波滤波器,其结构简单,易于实现,但是会产生相位滞后,使系统稳定性变差。20世纪80年代后,第二代DP系统中经常采用卡尔曼滤波器,该方法的主要缺点是必须将船舶运动的动力学方程在一些给定的艏摇角度值上线性化,由于系统拥有15个状态变量,所以采用上述方法时系统在线计算量大,而且其中的很多协方差值也很难调整,不利于实现[3~5]。
为了避免动力定位系统采用上述卡尔曼滤波器时所带来的问题,本文设计了一种基于无迹卡尔曼滤波器的改进算法对模型中的非线性函数的概率密度分布进行拟合,用一系列确定样本来逼近状态的后验概率密度,而不是对非线性函数进行线性化近似,因此对于非线性分布的统计量具有较高的计算精度。该滤波器的有效性通过仿真实验得到了验证。
2 基本的数学模型
2.1 船舶低频运动方程
船舶在海洋中的运动有六个自由度,而水面动力定位作业主要研究船舶的三自由度运动,即纵荡、横荡和艏摇。为描述船舶在水平面的运动,必须建立两个坐标系统[6~7]:惯性坐标系和随船坐标系,如图1所示,定义向量 η=[x,y,ψ ]T表示惯性坐标系下船舶的纵荡、横荡位置和艏摇角度,ν=[u,v,r]T表示随船坐标系下船舶的纵荡、横荡速度和艏摇角速度,两坐标系的相互转换关系为[8]

式中:转换矩阵


图1 固定坐标系和随船坐标系
由文献[8]可以得到船舶低速运动情况下的低频运动方程:

式中:M∈R3×3表示系统惯性矩阵,D∈R3×3为线性水动力阻尼系数。τ∈R3表示控制力和力矩,b∈R3表示由风、浪、流引起的环境力,wl∈R3为过程噪声向量。
2.2 高频运动模型
船舶的高频运动主要是由于一级波浪扰动引起的,可看作是在纵荡、横荡和艏摇三个方向上附加了阻尼的二阶谐波振荡器:

式中,参数 ki与海况有关,ζi(i=1,2,3)为相对阻尼系数,通常取值为 0.05~0.3,w0i(i=1,2,3)为波浪P-M谱中与有义波高相关的海洋主导角频率。
将上式转换为状态空间形式,可以得到船舶的高频运动模型:

式中 ξh=[ξx,ξy,ξφ,xh,yh,ψh]T
表示船舶在3个自由度方向上的位置和速度信号;wh为零均值高斯白噪声,wh=[wxwywφ];ηh为三维列向量,分别表示高频运动的纵荡、横荡和艏摇角度;其它系数为
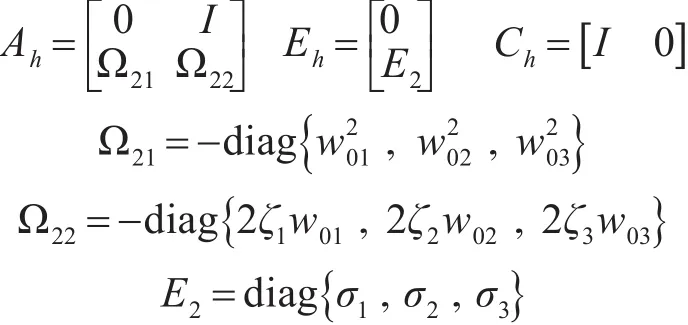
其中σi(i=1,2,3)为与波浪强度有关的常数。
2.3 环境作用力模型
环境力通常是指风、二阶波浪漂力、流对船舶的作用力。环境力模型由高斯—马尔科夫过程表示:
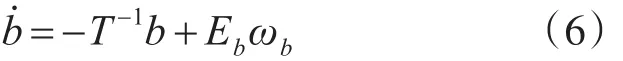
式中:b∈R3表示环境力和力矩;T为包含时间常数的的三维对角矩阵;Eb∈R3×3为噪声幅值矩阵;ωb∈R3为零均值高斯白噪声向量。
2.4 总系统模型
由前面的叙述可得系统的测量模型:

式中:vy∈R3为零均值高斯白噪声。
根据上述模型,综合得到总的动力定位船舶的数学模型:

3 非线性估计滤波器的设计
3.1 基本原理
基于无迹卡尔曼滤波的改进算法避免了对非线性系统线性化,而是在估计点附近进行UT变换,使用无迹变换来处理均值和协方差的非线性传递问题,将先验状态估计的Sigma点应用到测量更新中[9]。
3.2 基于无迹卡尔曼滤波的计算步骤[10]
1)初始化:给定系统状态的均值xˉ和方差P。
2)计算2n+1个Sigma采样点,这里的n指的是状态的维数:

3)计算这些采样点相应的权值

式中,小标m为均值,c为协方差,上标为第几个采样点。参数k是一个缩放比例因数,用来降低总的预测误差,a的选取控制了采样点的分布状态,待选参数β≥0是一个非负的权系数,它可以合并方程中高阶项的动差,这样就可以把高阶项的影响包括在内。
4)时间更新方程

式中,f(·)表示非线性过程,Qk为过程噪声在k时刻的方差。
5)根据一步预测值,再次使用UT变换,产生新的Sigma点集。

6)测量更新方程

其中,Zk为k时刻的观测值,H为观测矩阵,R为测量噪声的方差,K为卡尔曼增益。
3.3 基于无迹卡尔曼滤波器的设计
3.2 节中给出了算法流程,要把该算法应用到船舶动力定位系统中,需要确定算法中的时间更新方程和测量更新方程的第一个式子,这两个式子分别与总模型中的状态方程和观测方程相对应,基于无迹卡尔曼的改进算法在Matlab(R2013a)/Simu⁃link中搭建[11]并进行仿真实验。
图2中,Subsystem子系统是环境作用力模型,Subsystem1子系统是高频运动模型,J和J1是S-function模块。

图2 船舶动力定位系统Simulink模型
4 仿真与分析
为了验证算法的有效性,对非线性滤波算法进行仿真并与传统的卡尔曼滤波算法进行对比。本文在MATLAB(R2010a)软件上进行仿真实验,以某动 力 定 位 船 舶 为 例[12]:长 L=175(m),重m=2.461×104(kg),惯性矩阵M 和线性阻尼阵 D取值如下:

环境扰动作用力模型中的时间参数选为:T=diag(1000 1000 1000),波浪主频率、相对阻尼系数和波浪强度为:w0i=0.9,σi=0.6083,ζi=0.3。
所以高频运动模型中的系数矩阵取值为:

仿真时间为1000s,船舶运动和无迹卡尔曼滤波器对船舶纵荡、横荡和艏摇方向位置的滤波效果如图3~4所示。

图3 船舶的低频运动

图4 船舶的高频运动
图5 、图6和图7为使用传统的卡尔曼滤波时,船舶的纵向位移、横向位移和艏向角的真实值和估计值。图8、图9和图10为使用非线性滤波器时,船舶的纵向位移、横向位移和艏向角的真实值和估计值。从仿真结果可以看出,非线性滤波器从附有噪声和高频运动分量的综合输出中能够较好地滤除高频运动部分,图8~图10估计值较好地从真实值中估计出,使动力定位船舶能够得到有效的控制,减少不必要的能量损失。

图5 纵向位移真实值和估计值

图6 横向位移真实值和估计值

图7 艏摇方向真实值和估计值
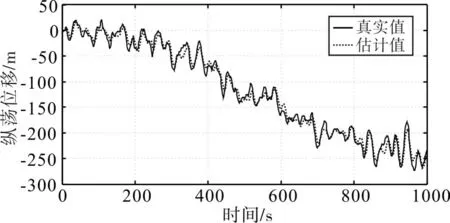
图8 纵向位移真实值和估计值

图9 横向位移真实值和估计值

图10 艏摇方向真实值和估计值
5 结语
本文针对船舶动力定位控制系统设计了一种基于无迹卡尔曼滤波器的非线性观测器,该观测器的优点是摒弃了对非线性函数线性化的传统做法,使用无迹变换来处理均值和协方差的非线性传递问题。仿真结果表明,该非线性观测器可以较好地估计船舶运动的各状态值,适用于动力定位系统。
[1]边信黔,付明玉,王元慧.船舶动力定位[M].北京:科学出版社,2011:8-10.
[2]Tomera,Miroslaw.Nonlinear observers design for multi⁃variable ship motion control[J].Polish Maritime Re⁃search,2012,19(S1):55-56.
[3]Grimble M J,Patton R J,Wise D A.The Design of Dy⁃namic Ship Positioning Control Systems Using Extended Kalman Filtering Techniques [C]//Oceans, 2011:488-497.
[4]J LI,G xia.The application of an extended Kalman filter in the dynamic positioning system[C]//International Con⁃ference on Natural Computation,2016:1945-1946.
[5]何黎明,田作华,施颂椒.动力定位船舶的非线性观测器设计[J].上海交通大学学报,2003,37(6):964-965.
[6]Bui VP,Ji SW.Nonlinear observer and sliding mode con⁃trol design for dynamic positioning of a surface vessel[C]// International Conference on Control, 2012:1900-1904.
[7]Du JL,Wang SY,Zhang XK.Nonlinear observer design for ship dynamic positioning system[J].Ship engineer⁃ing,2012,34(3):307-312.
[8]Thori.Fossen,Tristan Perez.Kalman Filtering for Position⁃ing and Heading Control of Ships and Offshore Rigs[J].IEEEControl Systems Magazine,2009,29(6):32-46.
[9]丁浩晗,冯辉等,基于自适应无迹卡尔曼滤波的动力定位估计状态[J].大连海事大学学报,2016,42(2):242-246.
[10][美]Dan Simon.最优状态估计—卡尔曼,H∞及非线性滤波[M].张勇刚,李宁,奔粤阳,译.北京:国防工业出版社,2013:334-336.
[11]黄小平,王岩.卡尔曼滤波原理及应用—MATLAB仿真[M].北京:电子工业出版社,2015:103-105.
[12]Saelid S,Jenssen N,Balchen J.Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control[J].Automatic Control IEEE Trans⁃actions on,1983,28(3):331-339.
