变电站选址智能算法研究
2018-02-05赵思雯姚天昊赵叙龙
赵思雯,叶 鹏,姚天昊,赵叙龙,牛 潇
(沈阳工程学院 电力学院,辽宁 沈阳 110136)
变电站选址对于电网规划来说是重要环节之一,电网结构、供电可靠性决定于变电站位置的选取。科学合理布置变电站布局不仅可以降低电能损耗,还可以节省建设投资。变电站的位置处于主网和配网的交汇点处,不仅是上级电网的负荷点,也是下级电网的电源处。变电站站址是电力系统规划的合理性的关键点,不仅对电力行业的经济效益起着至关重要的作用,还影响着整个电力系统的结构。科学合理地安排变电站站址,对电网的经济可靠性、安全运行意义重大。
近年来,由于电力行业的重要性越发明显,而且变电站选址涉及的因素很多,尤其是涉及到地理因素和其他不定性因素的影响,数学模型的建立也存在一些困难,因此在变电站选址方面学者们使用了不同的方法进行综合分析研究。文献[1]研究了在不同原则下,构建了新的组合模型,基于单源和多源连续选址计算模型的建立,应用于变电站选址中,并致力于得出满足负荷条件下变电站的最佳站址。文献[2]考虑地理空间信息因素和其他不定性因素,运用了电网地理信息系统(GIS)的信息管理与空间分析功能,了解到不同备选站址的信息,分析其实践可行性,并通过模糊模式识别理论建立模型,进行分析,确定备选选址的决定性指标以及处理数据的准确性。文献[3]通过智能遗传启发式算法解决变电站选址的问题,这种智能算法优点是分析简单、易于结论;缺点是一旦问题数据规模增大,计算精度也会相应降低。文献[4]通过模糊综合评判方法,先确定各因素的优先顺序,然后根据排序结果对最终决策进行分析研究。近年来,随着计算机技术的不断进步,许多学者对变电站选址方法进行了创新。一些智能优化算法用于解决变电站选址的优化选址问题,例如,蚂蚁算法、遗传算法、微分进化算法、粒子群算法等。专家分析研究这些智能算法取得了很大的进展[5-8]。该文将主要通过对微分进化算法、粒子群算法这两种现代智能典型算法以及其他相关算法进行分析研究,总结各种算法在变电站选址中的应用并分析这些模型与算法存在的问题与不足。
1 微分进化算法
1.1变电站选址模型
为了满足变电站和线路投资费用最低,以变电站和运营费用最低,以此构建变电站选址模型。确定变电站的位置和数量,并规定变电站负荷低于其规定最大负载。具体的数学模型为
minC=C1+C2+C3+C4
(1)
s.t.
(2)
dij≤dmax
(3)
(4)
(5)
(6)
C4=μ(xi,yi,Si)
(7)
式中,i=1,2,…,N;Si为变电站i的容量;rt为同时率;r0为贴现率;α为投资因数;β为网损因数;N为变电站的总和;m为变电站的寿命;f(Si)及u(Si)分别为变电站的投资和运营成本;rimin为变电站最小容载比;n为所需投建变电站低压侧线路的寿命;(xi,yi)为变电站站址的地理坐标;(xj,yj)为空间分布负荷的地理坐标;dmax为最大的允许供电半径。
1.2 变电站选址步骤
变电站选址规划优化问题中引入微分进化(DE)算法,并采用参数动态调整策略,使其在计算初期保证群体的多样性,后期加快算法的寻优速度,从而加强DE算法的优势,变电站选址DE算法流程如图1所示。
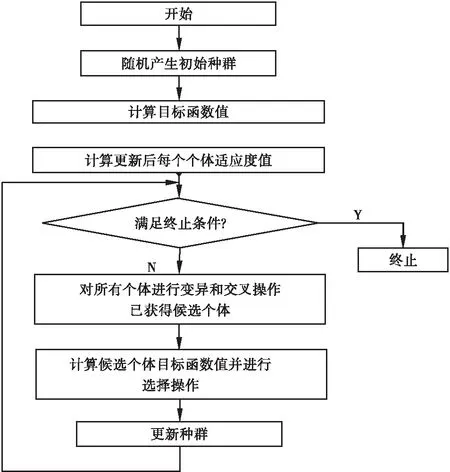
图1 DE算法流程
1.3 微分进化算法的应用
微分进化算法是1995年由Rainer Storn和Kenneth Price提出。微分进化算法与遗传算法比,优点是进化速度快、操作简单;但二进制编码困难,参数设置也没有统一。该方法先进行初始化站址,通过地理信息,再对变电站站址选址进行规范操作,最后用外点法构建函数,将状态变量引入目标函数中,经过变异、交叉等步骤后,最终确定站址和容量[9-14]。
2 粒子群算法
2.1 变电站选址模型
变电站选址问题的影响因素多样且繁琐。通常情况下,变电站会以投资费用的多少来确定变电站的个数、位置。在投资费用最少的情况下,要求保证可靠性水平,并且满足规划年负荷条件要求。
变电站容量和新建变电站的投资和运行费用都会在优化选址之前确定,而此模型的优化是为了满足线路和损耗的要求,如式(8)所示:

(8)
约束条件如式(9)~(12):
变电站容量约束:
(9)
供电半径约束:
dj (10) 地理条件约束: dik (11) (12) 式中,dj为变电站与负荷点之间的线路长度;r0为贴现率;N为待建变电站个数;Li为单位长度线路投资费用;J为变电站所供用电负荷集合;α为线路网损计算系数,U为线电压;cosθ为功率因数;(xi,yi) 和(xj,yj) 分别为变电站位置坐标和用电负荷点的位置坐标;D为最大允许供电半径;P为惩罚因子[15-16]。 初始化时,速度矩阵和解值矩阵是随机产生的,不确定的。而实际程序设计中,两者间可以没有直接联系[17]。应用粒子群算法的变电站选址流程如图2所示。 粒子群算法(PSO)是模拟鸟群觅食行为,通过仿生演化而来的计算方法。其本质是通过对当前位置、全局极值和个体极值的具体分析来共同指导粒子下一步迭代位置。PSO具有容易实现、收敛速度快的优点,但是也会有一定的问题出现,例如复杂情况下,容易早熟收敛、局部寻优能力较差。文献[15]提出一种解决配电网络变电站选址定容问题的方法,通过改进的多组织粒子群优化算法(RMPSO)来实现。根据站址、规划地块、湖泊、建筑物等信息,来判断变电站站址是否在规划区域范围内。变电站的容量、位置,以及地理信息等因素结合起来便会寻找到变电站最优站址。专家实例比较典型的PSO进行单源选址和改进的PSO两种方式,结果表明改进PSO算法更优化,使寻优复杂度降低,同时选址结果更加科学合理[18-22]。 图2 基于粒子群算法的变电站选址流程 Voronoi图是俄国数学家G.Voronoi在1908年提出的,又可以称为泰森多边形。该算法适合在地理信息的分析中。对于变电站规划问题,可以利用计算几何Voronoi图方法进行分析。文献[23]结合了选取变电站站址的原则,并充分利用该方法的优势,来选择新建变电站站址。在负荷均匀分布和非均匀分布两种情况下,根据现有变电站,选择新的变电站站址。但该文献没有限制变电站容量范围,如果得到的变电站容量超出备选容量,使规划结果不合理。文献[24]根据变电站现有的情况分析,给出改进的V图法,改进的算法将规划区域面积和负荷分布情况的坐标等因素综合在一起,得到初始站址。通过计算得出,该方法操作较复杂,并且由于固定站址数的等分方法,使得输出的初始站址偏离负荷中心。文献[25]提出一种基于粒子群优化的变电站规划方法。根据规划的优化技术得到新建站的容量组合,确定变电站站址和供电范围;根据每个粒子的位置作为变电站站址。 布谷鸟算法(CS)是由Yang和DEB Suash在2009年提出的一种启发式全局优化算法。该算法受到布谷鸟抢占其他鸟类巢穴,并寄生繁殖的行为启发,模仿一些鸟类的飞行行为构成的一种高效寻优方式。CS算法的优势是参数少、操作简单、搜索效率高、随机搜索路径优和寻优能力强,故已被广泛应用于各个领域,成为继GA和PSO之后的一种新的启发式算法[26-30]。基于布谷鸟搜索算法的变电站选址流程如图3所示。 图3 基于布谷鸟搜索算法的变电站选址流程 通过对微分进化算法、粒子群算法这两种现代智能典型算法以及其他相关算法进行分析研究,总结各种算法在变电站选址中的应用并分析这些模型与算法存在的问题与不足,为各位读者在今后工程实践中提供参考。 [1] 周 敏,程浩忠,周中明.优化理论在城市配电网变电站选址中的应用[J].供用电,2003,20(2):7-10. [2] 杨丽徙,王家耀,贾德峰.等.GIS与模糊模式识别理论在变电站选址中的应用[J].电力系统自动化,2003,27(18):87-89. [3] 李鑫滨,朱庆军.变电站选址定容新模型及其遗传算法优化[J].电力系统及其自动化学报,2009,21(3):32-35. [4] 贾德峰,许轶珊,任 群.用模糊综合评判法评价变电所所址[J].河南科学,2003,21(3):2-3. [5] 王成山,刘 涛,谢莹华.基于混合遗传算法的变电站选址定容[J].电力系统自动化,2006,30(6):30-34,47. [6] 付 郁.基于放进遗传算法的某发动机T装配线平衡研究[J].机械,2014(5):16-21. [7] 赵 强,敬 东,李 正.蚁群算法在配电网规划中的应用[J].电力自动化设备,2003,23(2):52-54. [8] 赵思雯,叶 鹏.基于AHP和熵权法赋权的变电站选址研究[J].沈阳工程学院学报:自然科学版,2017,13(3):244-252. [9] 朱卫平,刘自发.基于GIS和微分进化算法的变电站选址及定容[J].电力系统自动化,2007,31(18):82-86. [10]许童羽,孙艳辉.基于GIS和改进微分进化算法的农网变电站选址定容[J].电力系统保护与控制,2009,37(22):34-39. [11]STORN R,PRICE K.Differential Evolution-a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,Kluwer Academic Publishers,1997,11(4):341-359. [12]STORN R.System Design by Constraint Adaptation and Differential Evolution[J].IEEE Trans on Evolutionary Computation,1999,3(1):22-34. [13]王成山,魏海洋,肖 峻,等.变电站选址定容两阶段优化规划方法[J].电力系统自动化,2005,29(4):62-66. [14]马 威.基于GIS及改进微分进化算法的变电站选址研究[J].机电工程,2015,32(5):685-689. [15]董永峰,杨彦柳,宋 洁.基于改进粒子算法的变电站选址规划[J].继电器,2008,36(5):32-35. [16]刘自发,张建华.基于改进多组织粒子群体优化算法的配电网络变电站选址定容[J].中国电机工程学报,2007,27(1):105-111. [17]徐珍霞,顾 洁.离散粒子群优化算法在变电站选址中的应用[J].电气应用,2006,25(4):35-28,115. [18]严司玮,姚建刚,李丰涛.基于改进粒子群算法的变电站两阶段优化选址[J].2010,38(5):34-38. [19]杨明海,刘 洪,王成山.基于粒子群文化算法的变电站选址与定容[J].2012,45(9):785-790. [20]REYNOLDS R G.On modeling the evolution of Hunter Gatherer decision-making systems[J].Geographical Analysis,1978,10(1):31-46. [21]REYNOLDS R G.An Adaptive Computer Model of the Evolution of Agriculture for Hunter-Gatherers in the Valley of Oaxaca,Mexico[D].Ann Arbor:University of Michigan,1979. [22]陈 颖,徐晓辉,李志全.基于免疫克隆原理的改进粒子群优化算法的研究[J].系统仿真报,2008,20(6):1471-1474. [23]关洪浩,唐 巍.基于Voronoi图的变电站选址方法[J].电力系统保护与控制,2010,38(20):196-200. [24]葛少云,李 慧,刘 洪.基于加权Voronoi图的变电站优化规划[J].电力系统自动化,2007,31(3):29-34. [25]路志英,葛少云,王成山.基于粒子群优化的加权伏罗诺伊图变电站规划[J].中国电机工程学报,2009,29(16):35-40. [26]周培德.计算几何-算法分析与设计[M].北京:清华大学出版社,2000. [27]邵 萌,李郁霞.基于布谷鸟搜索算法的变电站选址方法研究[J].电网与清洁能源,2016,32(11):51-61. [28]明 波,黄 强,王义民.基于改进布谷鸟算法的梯级水库优化调度研究[J].水利学报, 2015,46(3):341-349. [29]叶 峰.基于人工智能方法的变电站选址定容规划研究[J].科技资讯,2011,32:112-113. [30]CARRERAS B A,LYNCH V E,DOBSON I.Critical points and transitions in an electric power transmission model for cascading[J].Chaos,2002,12(4):985-994.2.2 变电站选址步骤
2.3 粒子群算法的应用
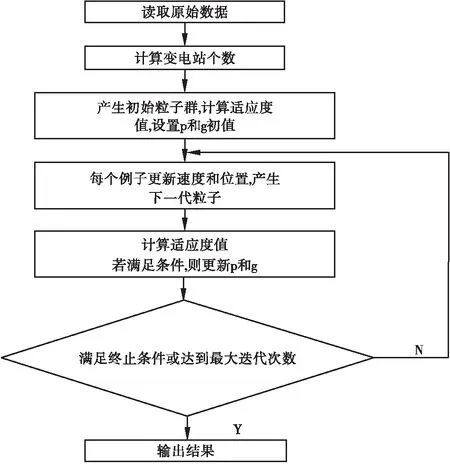
3 其他智能优化算法在变电站选址中的应用

4 结 论
