直角坐标机器人刚柔耦合动力学仿真分析

陈 骏，陈 威

(安徽博微长安电子有限公司，安徽 六安 237010)

直角坐标机器人作为柔性自动化设备广泛应用于焊接、码垛等领域。由于实际工况复杂多变，具体使用条件的差异会导致直角坐标机器人动态性能出现较大变化[1]，长时间工作会对其可靠性产生较大影响。

本文从影响直角坐标机器人动态性能的诸多因素中选取工作速度和负载进行研究。将直角坐标机器人关键构件柔性化处理，并构建刚柔耦合模型，进行动力学仿真，研究工作速度和负载与直角坐标机器人末端振动的关系，为提高直角坐标机器人动态性能提供参考。

1 直角坐标机器人刚柔耦合动力学建模

1.1 刚柔耦合多体系统动力学方程

直角坐标机器人在运动过程中存在刚体大范围运动与柔性体弹性变形相互耦合的情况[2]。本文分别建立柔性体和刚体模型，采用Craig-Bampton法进行减缩，建立直角坐标机器人刚柔耦合多体系统动力学方程。

1.1.1 基于绝对节点坐标法的柔性体模型

柔性体k由多个梁单元j组成，单元上任意一点的全局位置为：

rkj=Skjekj

(1)

式中，Skj为单元形函数；ekj为单元节点的广义坐标矢量。

梁单元j的弹性势能为：

(2)

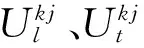
根据虚功原理，梁单元j的动力学方程为：

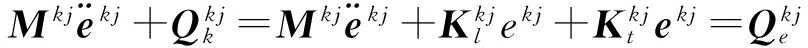
(3)

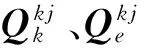
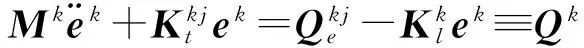
(4)

采用Craig-Bampton法将广义坐标矢量ek减缩为：

ek=Tkqk

(5)

将式5代入式4中，等式两边左乘TkT，则有：

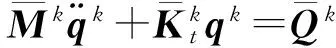
(6)

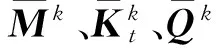
1.1.2 基于自然坐标法的刚体模型

刚体i的动力学方程为：

(7)

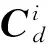
1.1.3 消除线性约束[3]的刚柔耦合多体系统动力学方程

由式6和式7得到刚柔耦合多体系统动力学方程为：

(8)

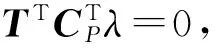
刚柔耦合多体系统动力学方程可简化为：

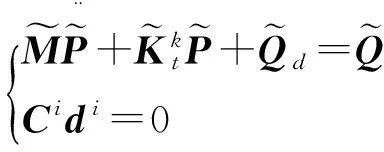
(9)

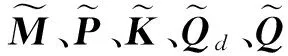
1.2 直角坐标机器人刚柔耦合模型

为提高后续仿真精度，应用ANSYS和ADAMS软件将直角坐标机器人中的十字滑座和Z向滑枕进行柔性化处理，输出模态中性文件。柔性化的步骤如图1所示。

图1 刚柔耦合模型的建立过程图

经过柔性化处理后的十字滑座和Z向滑枕如图2所示。进行刚柔替换得到的直角坐标机器人刚柔耦合模型如图3所示。

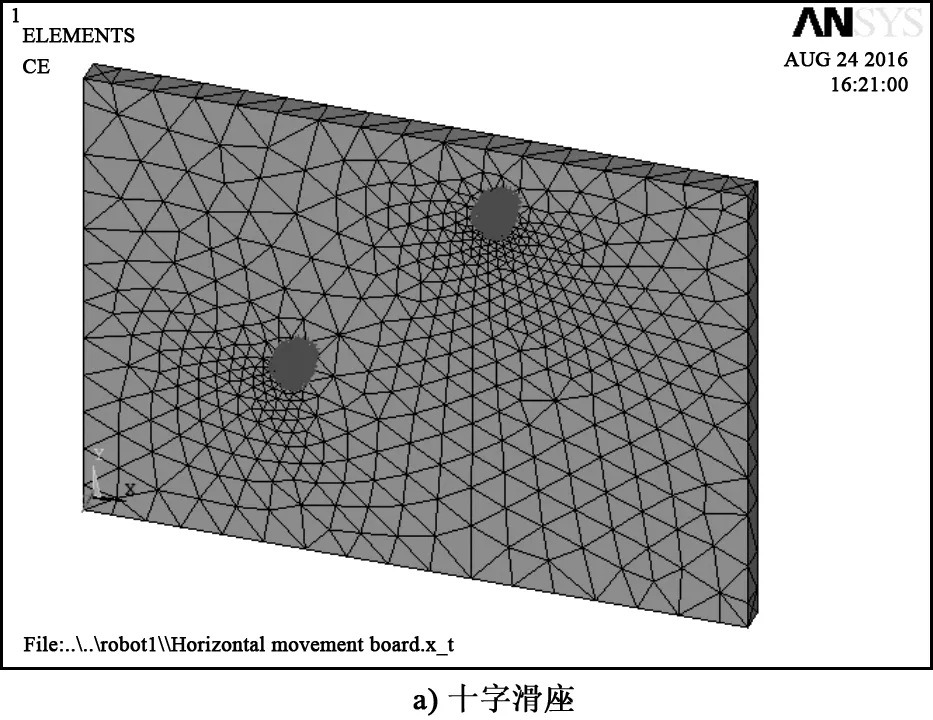
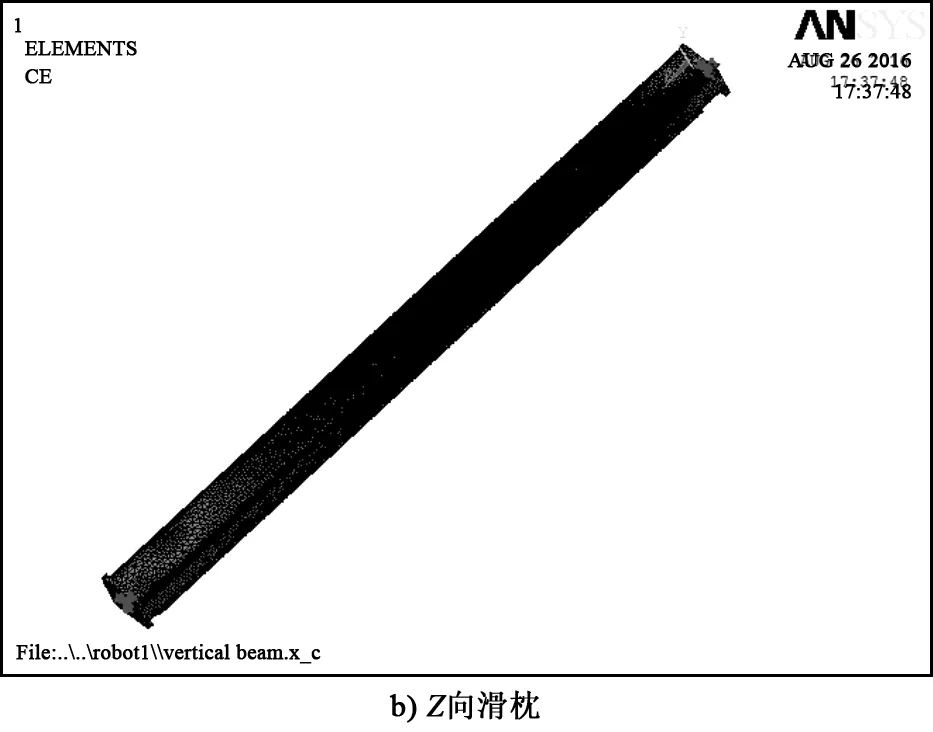
图2 柔性化的十字滑座和Z向滑枕

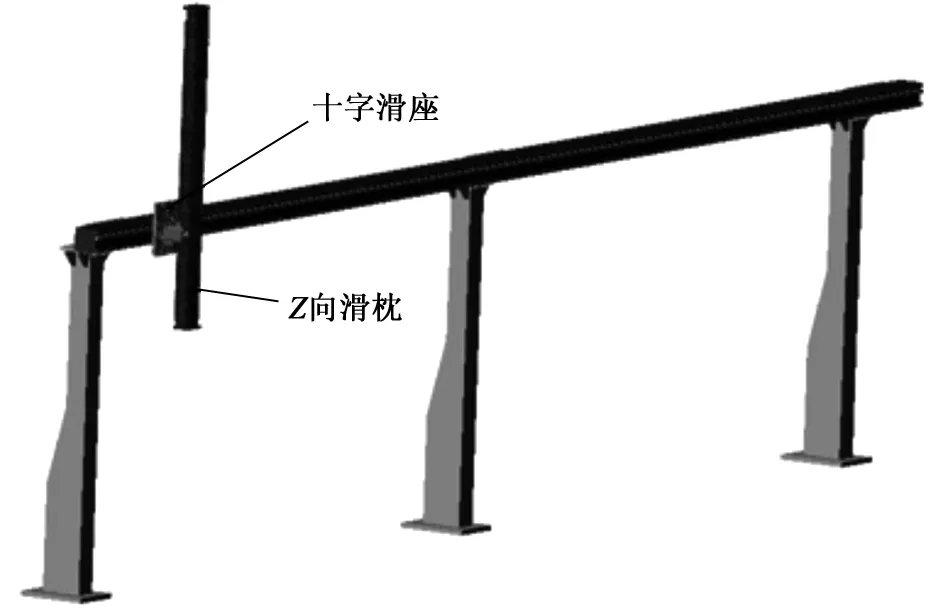
图3 直角坐标机器人刚柔耦合模型

2 动力学仿真分析

以直角坐标机器人末端的加速度作为比较参数，选取直角坐标机器人沿X轴方向运动进行分析，采用控制变量法进行不同工作速度和不同负载下的动力学仿真。

2.1 不同工作速度下的动力学仿真

将直角坐标机器人手爪系统及抓取负载简化为等效质量块，定义Z向滑枕末端中心为直角坐标机器人末端，添加MARKER_12作为加速度的测量点，行程设置为2 000 mm。

保持负载不变，分别设置200、400、600、800和1 000 m/s等5种不同的工作速度，仿真步长设为0.002，得到不同工作速度下直角坐标机器人末端X方向的加速度曲线(见图4)。

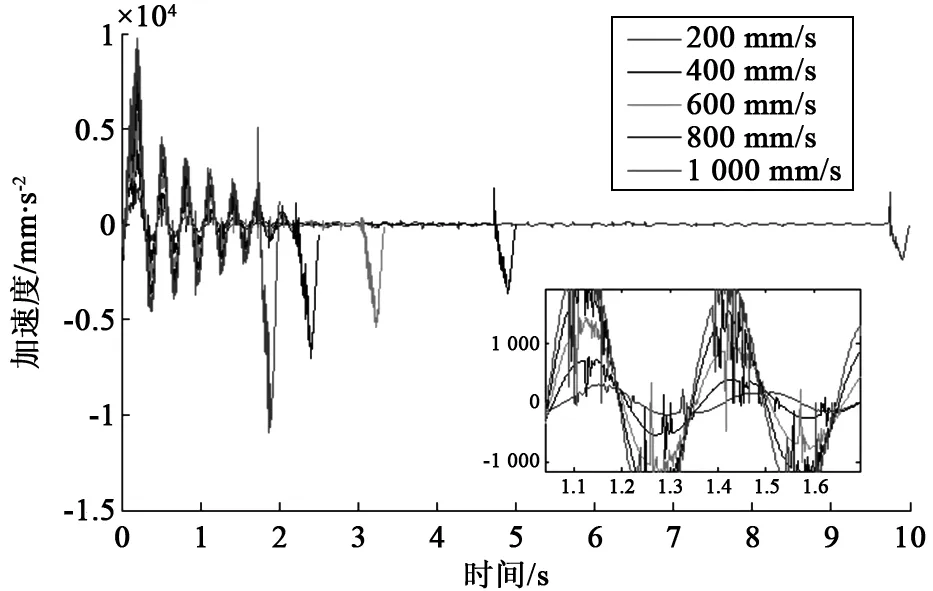
图4 不同工作速度下直角坐标机器人末端X方向加速度曲线图

由图4可知，在匀速运动阶段，直角坐标机器人末端X方向的加速度幅值随工作速度的增大而增大。

2.2 不同负载下的动力学仿真

将工作速度设为300 mm/s，分别设置0、2、4、6、8和10 kg等6种不同负载，仿真时间设为6.66 s，得到不同负载下直角坐标机器人末端X方向的加速度曲线(见图5)。

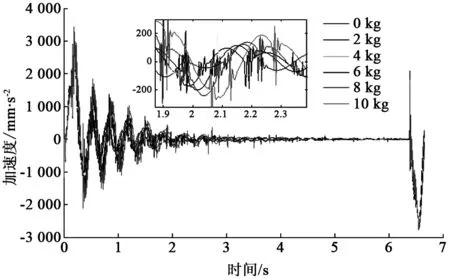
图5 不同负载下直角坐标机器人末端X方向加速度曲线图

由图5可知，在匀速运动阶段，直角坐标机器人末端X方向的加速度幅值随负载的增大而增大。

2.3 工作速度和负载对仿真结果的影响比较

在ADAMS软件中，设置成相同倍数的工作速度和负载进行动力学仿真[4]。首先，将负载设置为2 kg，得到工作速度分别为200和800 mm/s时直角坐标机器人末端X方向的加速度；然后，将负载设置为8 kg，同样得到上述2种速度下直角坐标机器人X方向的加速度。将规定条件下直角坐标机器人末端X方向的加速度绘制成曲线图(见图6)。

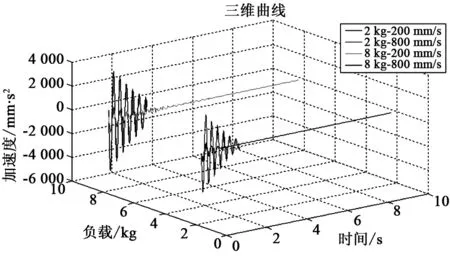
图6 规定条件下直角坐标机器人末端X方向加速度曲线图

由图6可知，当负载为2 kg，工作速度从200 mm/s提升至800 mm/s时，末端X方向的加速度绝对均值为变化前的18.94倍，而负载为8 kg时，加速度绝对均值为变化前的16.24倍；当工作速度为200 mm/s，负载从2 kg增大为8 kg时，末端X方向的加速度绝对均值为变化前的1.52倍，而工作速度为800 mm/s时，加速度绝对均值为变化前的1.30倍。

比较可知，在工作速度和负载同样增大4倍的情况下，工作速度变化对直角坐标机器人末端振动的影响更加明显。

3 结语

本文基于直角坐标机器人刚柔耦合模型进行动力学仿真，研究工作速度和负载与直角坐标机器人末端振动的关系。通过不同工作速度和负载下的动力学仿真，得到直角坐标机器人末端振动随工作速度和负载的增大而增大；比较规定条件下的直角坐标机器人末端X方向的加速度绝对均值，得到两者在同样增大4倍的情况下，工作速度变化对直角坐标机器人末端振动的影响更加明显。

[1] 何正嘉，曹宏瑞，訾艳阳，等. 机械设备运行可靠性评估的发展与思考[J]. 机械工程学报，2014，50(2):171-186.

[2] Garcia-Vallejo D, Escalona J L, Mayo J, et al. Describing rigid-flexible multibody systems using absolute coordinate[J]. Nonlinear Dynamics, 2003, 34(1/2):75-94.

[3] 孙东阳, 陈国平. 刚柔耦合多体系统动力学模型降阶[J]. 振动工程学报，2014(5):708-714.

[4] 王鑫, 史艳国, 张庆龄, 等. 高速和重载下刚柔耦合机器人动力学仿真[J]. 中国科技论文, 2016, 11(10):1100-1103.