一类HJB方程的迭代算法求解

李明伟 云南开放大学

在实践当中，HJB方程应用范围较广，涉及到科研、工程建设以及经济建设等多个领域，尤其是对一些最优控制问题的求解，常用的技术手段为动态规划，直接产生的形式为HJB方程。在这一过程中，对于一些非线性期权定价方面的工作，也可以使用HJB方程，完成问题的转换和解决，下面笔者结合相关方面的研究，对本课题进行详细论述[1]。

1 对一类HJB方程进行介绍

1.1 HJB方程数值解

对于HJB方程主要是对于有关方面研究的三位专家名字首字母的缩写，其具体形式如下所示：

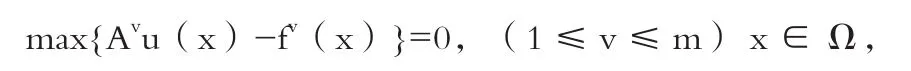
当u（x）=0时，x的取值范围在θΩ范围之内，在具体判定过程中，主要的依据是Ω是否属于Rn，如果在其范围之内，则可判断光滑，存在界域，将fv（x）从属于C2（Ω）设置为既定函数，那么Av可以被定义为二阶一致椭圆算子。在具体应用过程中，相关的求解方法源于动态规划原理[2]，而对于HJB方程的求解方法，最早出现的是对其进行离散化处理，使用的是有限元法或者限差方法，然后求解离散化方程的数值，具体步骤如下：

首先，当v属于1——m范围之内，进行方程组求解，将具体的解记做u0h，m.公式如下：

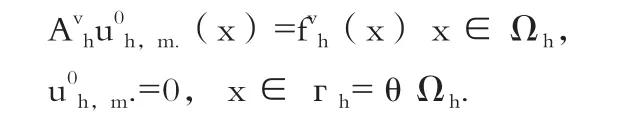
其次，在n值不小于1的情况下，且1≤v≤m时，给出条件为在这一过程中求解方程组，并将具体的解记做.需要求解的方程组如下所示：

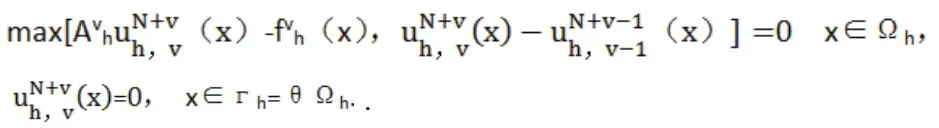
1.2 多重网格法

有关于多重网格法的基本思想体现在以下几点：通过实际的计算案例可以证明，需要使用常规单网格迭代模式，保证迭代法的科学性，促进椭圆型边值求解的准确和方便，收敛速度会随着迭代的进行逐渐减慢，之所以产生这一现象的主要原因是：相对网格步长，可以将初始误差分为低频光滑分量和高频摆动分量，只要松弛因子选择合理，高频分量的误差衰减效果将会较为明显，而对于低频分量，通过松弛因子的选择来提高误差衰减效果是不可能的，因此，可以总结为，采用固定的单网格迭代模式时，光滑的误差分量衰减速度较慢，降低了收敛速度。使用多重网格法就是为了消除这一隐患，根据网格尺度来划分，细网格上面被认定为低频光滑分量，粗网格上面被认定为高频摆动分量，在使用该方法的过程中，先进行细网格迭代，衰减掉相应的摆动分量，然后在粗网格上完成低频光滑分量的衰减，这样会早知网格逐渐加粗，消除各种误差分量，当处于最后层粗网格时，节点数量较少，可以通过直接解法计算，最后通过粗网格逐步返回各层细网格开始计算，经过多次计算，得到所需的数值[4]。

1.3 瀑布型多重网格法

根据多重网格法，相关人士研究出了瀑布型多重网格法，这一方法的优点体现在，无需在粗网格上面完成校正工作，具有单向性。在具体操作过程中，当迭代发生在细网格之上时，与粗网格之间存在关联性的误差将会降低频率，由高频转化为低频，无法实现通过磨光算子来减小的目标，因此，要保证使用瀑布型多重网格法时，每层求解的精度要满足最细网格的要求，致使粗网格上面发生较多的迭代。对于瀑布型多重网格法的最优化评价指标是误差估计保持在能量范数以下，这是该方法的不足之处，而这一方法的优势体现在简捷、对于每层所发生的迭代可以进行预先确定，主要依据是最细网格层数与当前网格层数之差，并不依据空间维数来判断，因此，可以用于高维问题的解决，能起到理想效果。

2 迭代法及其收敛性的介绍

在具体分析过程中，以max1≤j≤k{Aj（u）-Fj}=0为例进行具体分析，其中K是Rn的子集，并将K到Rn的算子记做A，对于在（v1，v2...，vn）T∈Rn范围内的每一个v值用v++v-来表示，对于v+代表的是max{v，0}，v-代表的是min{v，0}，其中最大值和最小值的选取依据为分量情况，Fj从属于Rn，对于T的单调函数记做Aj，对于j的取值范围在{1，2，...k}之间。

在讨论收敛性的过程中，如果v∈Rn且满足：max{AJ（u）-Fj}≥0，（1≤j≤k），这时可以将v定义为max1≤j≤k{Aj（u）-Fj}=0迭代算法中的一个上解，并将所有上解组成一个集合，称之为上解集，用S来表示。

具体算法如下：

第一步，对相关条件进行设置，假定ε＞0，u0属于S上解集合范围，m：=0.

第二步，对l取值为{1，2，...n}等不同情况进行计算，计算对象为ulm+1，计算目标主要是实现max1≤j≤k{(Aj（um+1，l）-Fj)l}=0，在这一环节当中，对于um+1，l要包含在{u1m+1，...ulm+1...ul+1m，..unm}范围之内。

第三步，假设um+1与um+1，n相等，如果ε＞‖um+1-un‖，那么停止计算，否则，将m：=m+1，回归到第二步重新开始计算。

相关的引理如下：

设置A属于K上面的连续单调函数，将N的子集合设置为I和J，且二者之间的关系为J=N/I。所有属于K范围内的y和z，如果满足yI=zI，与此同时，还要保证yJ≥zJ，这时，得出的结论是AI（z）≥AI（y）。对其进行论证，主要表现在以下方面：

只要保证y，z属于K范围之内，并且保证yI=zI，与此同时，还要保证zJ≥yJ，在这种情况下，假设I∧={j∈I：A（jy）＞Aj（z）}，且还要求=，并且对于I∧的情况进行限定，务必保证非空。

在w2=y的情况下，对于w1的定义主要分为两种情况，当时，（w1）j=zj+δ，当时，（w1）j=zj，在这一过程中，δ取值为正数，并在函数A的连续性支持下，δ取值可以足够小，这样就可以得出，一切满足的情况下，都可得出Aj（w2）＞Aj（w1），对这一结论进行总结，结果有两种，其一，当，（w1-w2）j+=δ，其二，当时，（w1-w2）j+=0，所以，在此情况下，可以推论出：（Aj（w1）-Aj（w2））＜ 0 与（A（w1）-A（w2），（w1-w2）+）≥0相等，这是一个矛盾结果，所以，当与Φ相等时，Al（z）≥ Al（y）。

3 区域分解法

区域分解法可以实现对大规模问题的分析和解决，并可以进行并行计算，下面对其收敛性进行验证，假设N=N1∪N2∪N3∪N4...∪Nq，其中q的取值为正数。

具体算法如下：

第一步，进行条件设定，假定ε＞0，u0属于S上解集合范围，m：=0.

第二步，在p=1，2，3，4，...，q的情况下，分别进行并行计算，求出非线性方程组解，

um+1，p 属 于 Qpm+1， 结 果 如 下：max1≤j≤k{(Aj（um+1，p）-Fj)Np}=0，在这一环节当中，对于Qpm+1，要满足与{v∈Rn：vs=usm，s∈N/Np}相等.

第三步，对um+1进行取值的最小化，使其等于min{um+1，p}，在这一过程中，p的取值要满足在{1，2，3，...q}范围之内.

第四步，假设ε＞‖um+1-um‖，那么停止计算，否则，将m：=m+1，回归到第二步重新开始计算。

4 结束语

综上所述，有关于一类HJB方程的迭代算法求解方法较多，随着研究的不断深入，对原有的求解方法在不断更新和改进，但总体的原则是务必保证求解的准确性，且要求简化求解过程的计算量，根据相关解法的优劣势进行对比分析，互相借鉴，满足实际需求。除此以外，研究人员，还要明确研究方向，以现实问题的解决和发展趋势为主要目标，对于一类HJB方程的迭代算法求解进行创新，为相关方面的工作开展奠定基础。

[1]谢水连，许鸿儒，胡汉章.求解一类HJB方程的迭代算法[J].高校应用数学学报，2012，27(2):000200-205.

[2]杨建鹅，黄晓梅.求解HJB方程的两类迭代法研究[J].江西科学，2014，32(2):185-188.

[3]邹战勇，周叔子.求解HJB方程的拟变分不等式组的迭代法[J].应用数学学报，2012，35(4):747-755.

[4]梁莉，李胜军.一类HJB方程的上解和下解[J].兰州文理学院学报(自然科学版)，2013，27(6):18-20.