基于数学模型的风电场运行问题研究

周 千

(西安航空学院 理学院，西安 710077)

0 引言

风能是指地球表面大量空气流动所产生的动能。作为一种清洁的可再生能源，风能越来越受到人们的重视。风力发电是把风的动能转化为电能的一种应用形式。我国某风电场已先后进行了一、二期建设，现有风机124台，总装机容量约20万千瓦。本问题源自于2016年全国大学生数学建模竞赛D题。请讨论以下问题：

(1)原题给出了该风电场一年内每隔15分钟的各风机安装处的平均风速和风电场日实际输出功率。试利用这些数据对该风电场的风能资源及其利用情况进行评估。

(2)原题给出了该风电场几个典型风机所在处的风速信息，同时，风机生产企业还提供了部分新型号风机，试从风能资源与风机匹配角度判断新型号风机是否比现有风机更为适合。

(3)为安全生产需要，风机每年需进行两次停机维护，两次维护之间的连续工作时间不超过270天，每次维护需一组维修人员连续工作2天。同时风电场每天需有一组维修人员值班以应对突发情况。风电场现有4组维修人员可从事值班或维护工作，每组维修人员连续工作时间(值班或维护)不超过6天。请制定维修人员的排班方案与风机维护计划，使各组维修人员的工作任务相对均衡，且风电场具有较好的经济效益。

1 风能资源及其利用情况的评估

从风功率密度、季度功率比以及我国风能区域划分标准三方面对该风电场的风能资源及其利用情况进行评估。

定义1：风功率密度，是指与风向垂直的单位面积中风所具有的功率。风功率密度越高，就代表风能资源越好，风能利用率也更高。

切入风速是指风力发电机组开始并网发电的最低风速，切出风速是指风力发电机组并网发电的最大风速，切入风速到切出风速之间的风速称为有效风速。

平均风功率密度和有效风功率密度是评估风能资源的重要参考数据，用如下两种方法对其进行求解。

方法1：利用实测数据计算

平均风功率密度表达式为：

(1)

其中Dj表示某季度平均风功率密度(W/m2)，n表示某季度内风速的记录数，ρ表示风电场空气密度，vi表示某季度内第i个记录的风速值。

有效风功率密度表达式为：

(2)

其中wj表示某季度有效风功率密度(W/m2)，m表示某季度内有效风速的记录数，vg表示某季度内第g个记录的有效风速值。

方法2：利用威布尔分布模型[1]计算

通过分析风电场实际测得的风速数据可得到该风电场风速的风频分布，它是评估风能资源分布情况的重要参数，威布尔分布是国内外很多学者认为适合描述风速分布情况的一种较好模型，其风速的概率分布密度函数为：

(3)

式中v为风速，k为威布尔分布的形状参数，c为威布尔分布的尺度参数，对公式(3)进行积分，可得到威布尔概率分布密度函数F(v)。

(4)

(5)

根据威布尔分布的均值和方差关系式可得：

(6)

(7)

得到威布尔分布后，某季度平均风功率密度计算公式如下：

(8)

某季度有效风功率密度计算公式如下：

(9)

式中vt为切入风速，即有效风速区间下限，vc为切出风速，即有效风速区间上限，利用公式可求得具体数据。

定义2：季度功率比，已知该风电场日实际输出功率，通过对每季度平均功率的计算，与总装机容量进行数量比，得到季度功率比。以此作为评估每个季度风能资源利用率的标准，功率比越大，表明该季度的风能资源利用率越高。

计算季度功率比的步骤如下：

(1)计算月平均功率Pi；

(2)计算季度平均功率Pj；

(3)计算季度功率比Qj；

风能划分标准：将我国划分为四种风能分区，分别为风能资源丰富区、 次丰富区、可利用区和贫乏区，如表1所示。以年有效风功率密度和年平均风速参数对某地区的风能资源进行评估。

表1 中国风能分区表

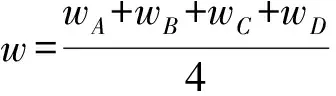
2 判断不同风机的匹配度

定义3：风机容量系数是指风机年平均输出功率与额定功率的比值[2-4]。

风机容量系数越大，风机效率越高，因此可用风机容量系数来判断新机型是否合适，针对风机容量系数的计算，建立以下模型：

风机输出功率：

(10)

式中P(v)为风机输出功率，Pr为风机额定功率，vi为切入风速，vr为额定风速，vc为切出风速。

威布尔分布函数：

(11)

式中Pw(v)为威布尔分布函数，其中k为形状参数，c为尺度参数，根据平均风速与最大风速估计出参数k=1.636,c=6.26。

风机年平均输出功率：

(12)

风机容量系数：

(13)

对该模型进行求解，得到新机型与旧机型的风机容量系数，通过容量系数与额定功率的比较，选出更加合适的机型。

3 排班方案与风机维护计划的制定

题目要求风机每年需进行两次停机维护，两次维护之间的连续工作时间不超过270天，每次维护需一组维修人员连续工作2天。为方便计，假设一年有360天，以2天作为一个周期进行维护、值班、休息，则共有135个周期。

由第一问结论知冬季风能资源最丰富，风能资源利用率最高。

已知12月有31天，1月有31天,2月有28天，冬季共有90天，选取3-11月，共270天作为维修人员的工作范围。

以风能资源损失最小为依据建立目标函数，尽量使维护工作在风能资源利用率较小的范围内进行，同时使人员工作任务相对均衡[5]。

目标函数如下：

(14)

式中i=1,2,3,4,j=1,2,3,…,135，Pj表示第j个周期的平均功率，Xij表示第 个小组在第j个周期的工作情况。

(1)由于风电场每天需有一组维修人员值班以应对突发情况，因此一个工作周期内至少有一组维修人员进行值班或维护工作，同时，一个工作周期内最多有两组维修人员分别进行值班和维护工作，其中，第i个小组在第j个周期的工作情况

(i=1,2,3,4,j=1,2,3,…,135)

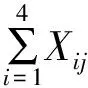
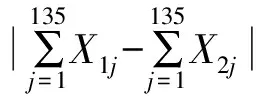
即约束条件如下：

利用lingo进行求解[6-7]，得到该风电场此年内需进行两次停机维护的工作周期。随后，对冬季3个月的90天，进行维修人员的值班工作安排。

4 模型的评价与推广

文中讨论了风电场的风能资源及其利用情况，并且从风能资源与风机匹配角度选出了更加适合风电场的风机型号，最后给出最优化的维修人员排班方案，具有较强的实用性。文中给出的风能资源及其利用情况的评估方法，以及最佳风机型号确定的方法，具有一定的通用性。模型仍然存在一些不足之处，比如在各步骤上，由于数据本身和算法实现都有一定的误差，导致对风能的评估结果产生了一定的误差。

[1] 杨贺钧.计及多因素的含风能电力系统可靠性评估及优化研究[D].重庆:重庆大学，2014.

[2] 杨星光.基于容量系数的风力发电机组选型研究[D].长沙：湖南大学，2012.

[3] 吴婷婷.风电场风能资源评估中重要参数的计算与应用[D].呼和浩特：内蒙古工业大学，2015.

[4] 华荣芹.基于风资源评估的风力机选型的研究[D].乌鲁木齐：新疆大学，2014.

[5] 杜俊涛.风电场值班的优化模型与算法模型[J].佳木斯大学学报(自然科学版)，2017，35(2)：317-320.

[6] 杨丹，赵海滨.MATLAB从入门到精通[M].北京：中国铁道出版社，2013.

[7] 袁新生,邵大宏,郁时炼.LINGO和EXCEL在数学建模中的应用[M].北京:科学出版社，2017.