基于滑模控制的光伏系统的最大功率点跟踪

， ,2，,2

(1. 西安工业大学电子信息工程学院，陕西 西安 710021；2. 西安工业大学自主系统与智能控制国际联合研究中心，陕西 西安 710021)

0 引言

尽管太阳能电池组件的成本相对较高，但由于其长期的经济前景和对环境保护的优势，太阳能以其取之不尽，用之不竭，不产生任何废弃物，没有噪声污染的特点，愈来愈受到关注、开发和利用。目前光伏(PV)电力系统成为太阳能主要利用方式之一，已经在世界各地商业化[1]。因此，如何快速地实现跟踪最大功率点跟踪MPPT成为光伏发电的研究热点[2]。

光伏(PV)电池在最大功率点(MPP)提供最大功率，而MPP的变化范围主要取决于光伏阵列的温度和日照强度[3]。目前，常用的最大功率点跟踪(MPPT)方法主要有：扰动观察法，其原理简单，易于实现，但是跟踪速度慢、对传感器精度要求不高，容易出现误判现象；电导增量法，其跟踪速度快、准确率高，但是需要处理大量数据，对于硬件的要求比较高；模糊控制法，其稳态精度较高、系统控制设计灵活、鲁棒性好，但动态响应较慢、适应能力有限、特定条件下易震荡[4-6]。以上这些方法都有一定的使用限制，使得系统无法快速且稳定地跟踪到最大功率点[7]。滑模变结构控制策略与常规控制的根本区别在于具有使系统结构随时间变化的开关特性。使得变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识，物理实现简单等优点[8]。

针对DC/DC功率变换器工作在开关管开通与关断状态具有变结构性的特点，基于光伏组件的特性，将扰动观察法的控制思想与滑模变结构相结合，提出了一种基于滑模变结构控制的MPPT方法。

1 工作原理

光伏电池本身呈现非线性I-V和P-V特性曲线，产生的最大功率取决于辐照和温度。基于光伏电池模块特征，MPP轨迹可以通过线性关系近似[9]。滑模控制是一种用于具有不确定性的非线性系统的有效的高频开关控制，对于控制开关模式转换器非常合适[10]，它具有强大的鲁棒性和快速响应性，明显优于线性控制器，并且在许多情况下易于实现。将两者特性比较分析后，发现该控制特性与光伏特性契合度较高，光伏电池具有非线性I-V和P-V特性曲线。产生的最大功率取决于辐射和温度，文献[9]根据光伏电池的I-V曲线，定义了一个只满足辐照的MPPT的滑模面：

S(V,I)=a·I-b·V+ref=0

(1)

V和I是光伏电池的输出电压和电流，a，b和ref这3个参数决定了开关表面，此时的开关面上不考虑温度的影响。

而温度是导致光伏电池特征曲线变化的另一个参数[11]。 图1表明温度变化对P-I曲线的影响。 如图1所示，对于给定的辐射，最大功率点的电流与温度无关，而温度变化导致P-I曲线中的MPP发生垂直变化。

图1 温度变化对P-I曲线的影响

考虑到这一点，图1中的距离ΔP为：

ΔP=αΔT

(2)

因此，新的MPP可以计算为：

Pmpp，new=Pmax-αΔTPmax

(3)

Pmpp,new为新的MPP；Pmax为最大功率点；α为温度系数；ΔT为温度差。结合式(2)和式(3)可以得到：

Pmpp,new=k1(1-αΔT)Impp

(4)

因此，考虑到光伏电池的P-I曲线，引入了一个新的最优切换面，同时满足辐射和温度的MPPT。在辐照度变化的情况下，所提出的滑模面如下：

S(P,I)=P-k1I+ref=0

(5)

P和I分别为光伏电池的输出功率和电流。

k1可以计算为：

(6)

Pmax和Impp分别为最大功率和最大功率下的电流。

因此，新的滑模面为：

S=P-k1(1-αΔT)I=0

S>0：ON

S<0：OFF

(7)

当S> 0时，主开关Sm1和Sm2接通，励磁电感Lm充电。 所以I增加，S(P,I)减少。 当S<0时，主开关Sm1和Sm2断开，存储在磁化电感中的能量流向负载; 因此，S(P,I)增加。所以，S(P,I)的变化始终围绕在S(P,I)=0的滑动切换表面。

2 系统结构与分析

2.1 拓扑结构

在光伏交流模块系统中，由于光伏发电模块和电网线路之间元件简单，隔离的优点，反相逆变器优先考虑在单相并网逆变器中[12]。微逆变器拓扑结构如图2所示。 它由2个开关反激转换器，展开桥和C-L滤波器组成。Sm1和Sm2是主电源开关。

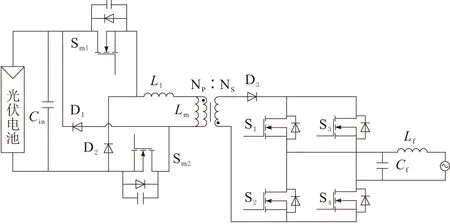
图2 微逆变器拓扑结构

D1和D2是钳位二极管;D3是整流二极管。Np和Ns分别是初级绕组和次级绕组。S1～S4形成全桥逆变电路，将整流的正弦波形并到电网。

2.2 参数选择

在选择匝数比的情况下，需要满足[13]：

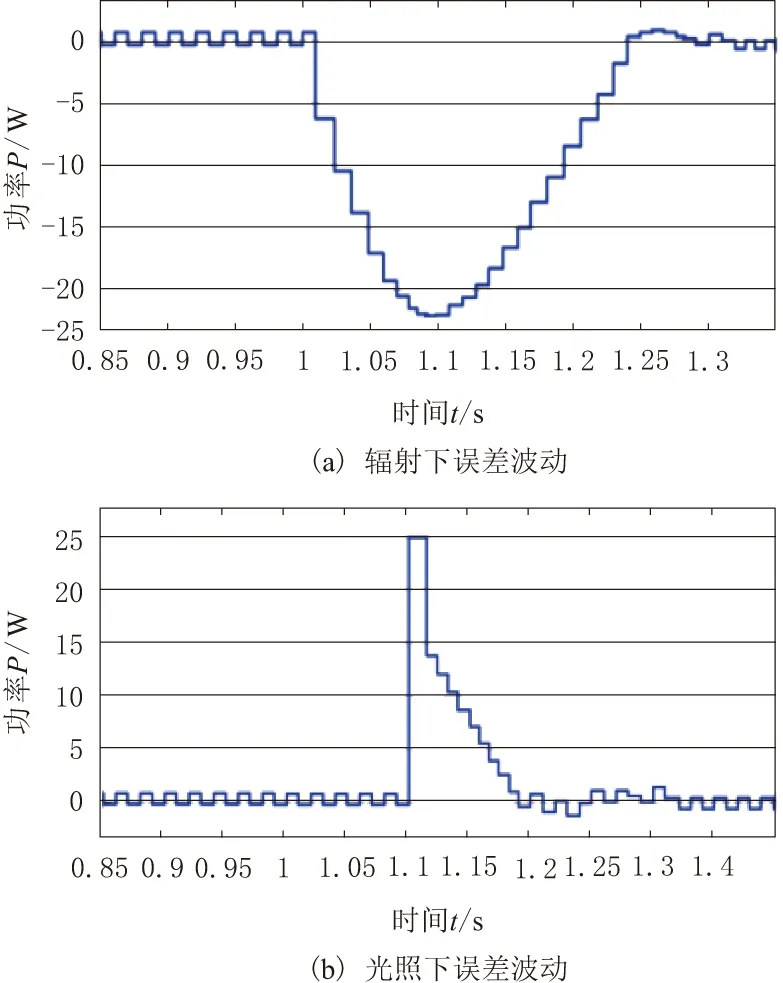
nVm

(8)

Vm为最大输出电压；Vin为输入电压；n为匝数比。满足上式不等式是为了防止主开关Sm1和Sm2断开时，D1和D2导通，将存储在Lm中的能量转移到源极。

为了确保微型逆变器始终在DCM下运行，最大占空比dmax应满足不等式：

dmax≤0.5

(9)

即

(10)

输入电压(MPP)：Vin= 50 V; 电网电压Vgrid=220 V; 电网频率fgrid=50 Hz; 开关频率fs=100 kHz;可得匝数比必须小于0.16。平均电流：

(11)

Ts为开关时间间隔。可得输入功率为：

(12)

可得PPV= 200 W，Vin= 50 V和dmax= 0.757，变压器初级电感最大值Lm,max= 9 μH;Lm= 0.8Lm,max= 7.2 μH。

当光伏电池稳定工作在其最大功率点时，逆变器输入功率Pin是恒定的，而逆变器的输出功率Po却是瞬变的，逆变器输入输出存在瞬间功率不平衡问题，反映在光伏电池输出侧表现为其输出电压包含有二倍频的扰动分量[14]。该扰动会影响最大功率跟踪的效率，降低对光伏电池的利用率。为此，应引入功率解耦方案抑制该二次扰动[15]，解耦电容的大小是：

(13)

3 仿真研究

为了验证所提出的MPPT方法的动态响应、稳定性和高效率，以及所提出的微逆变器拓扑的理论分析，用与MATLAB集成的PSIM 9.0软件进行了系统仿真，具体参数如表1所示。

表1 仿真系统参数

系统在辐射变化下和光照变化下基于滑模变结构扰动观察法时输出功率的波形，如图3所示。图3a纵坐标表示功率，横坐标表示时间，辐照度从1 000 W / m2降低到600 W / m2，环境温度25 ℃情况下，MPPT算法在0.2 s内收敛。图3b为辐照度1 000 W / m2，温度从25 ℃升高到55 ℃情况下，MPPT算法在0.1 s内收敛。图4纵坐标表示功率的误差波动，横坐标表示时间，显示了系统在辐射变化下和光照变化下基于滑模变结构扰动观察法时误差信号的波形，可以看出稳态下的波动幅度非常小。因此，在辐照度变化很大且光照条件增加的情况下，MPPT算法既满足快速响应又具有低稳态波动。

图3 输出功率波形

图4 误差波动波形

4 结束语

根据光伏电池的特性，将滑模变结构控制应用到光伏电池的MPPT中，提出新的切换面。该表面基于PV电池的P-I特性，并且同时满足辐射和温度。 此外，采用线性可变结构来降低稳态期间的输出功率波动，同时保持滑模控制器的快速响应和鲁棒性优点。仿真结果验证了采用滑模控制的MPPT具有快速稳定的性能。

[1] 颜景斌,王飞，王美静，等.改进滑模变结构控制光伏系统最大功率点跟踪[J].哈尔滨理工大学学报，2016，21 (4):106-111.

[2] 刘建光,方宇，王志彬，等.滑模控制在PV扰动法最大功率跟踪中的应用电力电子技术[J].电源学报，2012，10(1):90-93.

[3] 吴志鹏，卿湘运，杨富文，等.光伏发电系统的最大功率点跟踪算法及仿真研究[J].电源学报，2013，11 (4):20-25.

[4] 赵志.一种新的光伏系统最大功率跟踪控制方法[J].电源学报，2015，13(3):119-125.

[5] Eltawi M A ，Zhao Z.MPPT techniques for photovoltaic applications[J].Rrenewable and Sustainable Energy Reviews, 2013,25(3):793-813.

[6] Mohammadi S, Zarchi H A, Amiri M. Interleaved two-switch flyback microinverter for grid-tied photovoltaic applications[C]//Power Electronics, Drives Systems & Technologies Conference (PEDSTC), 2015:59-64.

[7] 何俊强.基于滑模变结构的光伏并网发电系统MPPT算法研究[D].济南：山东大学，2012.

[8] 刘金琨.滑模变结构控制MATLAB仿真基本理论与设计方法[M].北京:清华大学出版社,2015.

[9] Levron Y，Shmilovitz D.Maximum power point tracking employing sliding mode control[J].IEEE Transactions on Circuits and Systems I:Regular Papers，2013，60(3)：724-732.

[10] 汪义旺,曹丰文,张波,等. 基于温度系数在线修正的光伏MPPT[J]. 可再生能源,2013,31(8):100-102.

[11] Lascu C, Boldea I, Blaabjerg F.Very low speed variable structure control of sensorless induction machine drives without signal injection[J].IEEE Transactions on Industry Applications,2005,41(2):591-598.

[12] Kyritsis A C, Tatakis E C, Papanikolaou N.P.Optimum design of the current-source flyback inverter for decentralized grid-connected photovoltaic systems[J]. IEEE Transactions on Energy Conversion,2008,23(1):281-293.

[13] Zhang Z, He X F, Liu Y F.An optimal control method for photovoltaic grid-tied-interleaved flyback microinverters to achieve high efficiency in wide load range[J].IEEE Transactions on Power Electronics,2013,28(11):5074-5087.

[14] Tamyurek B, Kirimer B.An interleaved high-power flyback inverter for photovoltaic applications[J].IEEE Transactions on Power Electronics,2015,30(6):3228-3241.

[15] 高文祥,王明渝,王立健,等. 光伏微型逆变器研究综述[J].电力系统保护与控制,2012,40(21):147-155.