基于小波分析的脉冲激光回波抗干扰算法研究

，，

(西安工业大学电子信息工程学院，陕西 西安 710021)

0 引言

由于脉冲激光雷达具有主动探测目标、探测方向性强、不受电子干扰等优点，受到了广泛的关注。随着半导体和激光技术的发展，脉冲激光雷达技术也越来越成熟，目前己经初步实现工程化应用。但是由于云雾、烟尘等自然环境的干扰[1]，激光雷达后向散射回波信号会导致系统产生虚警。目前，在脉冲激光雷达抗干扰方面，国内外研究最多的是在光电探测方面，大都采用多波段复合探测和超窄脉冲激光等方法来提高激光的抗干扰性能，但实现这些技术需要更高性能指标的发射机和接收机，激光雷达的研制成本和难度也都会加大。因此，对脉冲激光雷达[2]云雾、烟尘回波特性进行研究是提高激光雷达抗环境干扰的有效手段，对提高脉冲激光雷达的工作可靠性具有重要意义。

在此，基于脉冲激光对真实目标和干扰目标[3]的回波差异进行分析，建立激光雷达回波模型，采用小波分析的方法提取出目标反射回波[4]，设计了基于小波分析的抗干扰算法，并进行了仿真验证，对脉冲激光雷达抗云雾干扰具有工程参考价值。

1 脉冲激光传输数学模型

1.1 后向散射模型

激光脉冲在大气传输过程中，云雾、雾霾等大气环境[5]都可看作是由米氏散射粒子组成的介质。由激光的大气传输特性可知，云雾中的悬浮粒子对激光脉冲传输具有衰减作用，并且发射的激光脉冲在大气中的衰减是由吸收和散射2个过程引起的。由于在云雾环境下，水汽悬浮体在近红外的波长区域，悬浮物体对激光的吸收可以忽略，因此，激光脉冲的衰减仅仅是由散射造成的。激光传输通过不连续的云雾等类似气溶胶时，一般情况下，接收机输入端上气溶胶干扰光学信号包络线变化特性函数为：

(1)

P为包络线函数，是后向散射激光到达接收端光电探测器上的强度；P0为接收端入射的激光光功率；S0为激光接收端入射口的表面面积；f(θ)为干扰颗粒后向散射方向函数；θ为接收机观察方向和反射表面法线的夹角；S(R)为接收、发射机视场几何图形的重叠面积；σs为气溶胶粒子的体积散射系数；R为距离；H2为气溶胶生成物边缘与接收机的距离；H1为辐射距离；H0为盲区深度；K=2/cτN为常数，其中，c为光速3×108m/s；τN为脉冲宽度。

1.2 目标反射模型

在近程探测下，目标物体表面通常比脉冲激光的光斑大。当激光光束面积小于被照物体表面面积时，来自被目标反射回来的激光回波功率P为：

(2)

T3为滤光片透过率；P1为激光峰值功率；ρ为目标表面反射率；R1为目标和接收机之间的距离；D为接收机孔径；T1为发射光学透过率；T2为接收机的透过率；R2为在激光和目标之间的距离；θ为接收机中心连线与目标物体表面法线之间的夹角。指数项是大气透过率，与目标物体距离以及大气消光系有关。

1.3 激光目标回波模型

对于特定的目标物体，其激光回波信号具有一定的稳定性。当激光照射到这类特定的目标上时，就会产生相应的反射，而对于烟尘目标，会产生2次散射，使得其回波信号扩展。激光回波信号展宽的主要因素是不同粒子[6]散射回波信号的叠加。发射脉冲激光在传输过程中，其中一部分激光光子穿透云雾后照射到目标上，被目标反射后穿过云雾被接收端探测器所接收。因为后向散射信号[7]先到达接收端，目标回波信号[8]后到达接收端，当目标物体[9]距离激光雷达较近时，2个回波信号会相互叠加，因此脉冲激光雷达的回波信号具有2个峰值。

由于在无大气干扰条件下单个脉冲激光回波波形表现为高斯脉冲[10]，大气后向散射回波波形也表现为钟形状态，因此一般的激光目标回波信号波形可以表示为：

(3)

Hi为回波的幅值参数；σi为回波信号的宽度参数；N为叠加的回波信号数；ki为第i个回波的峰位置。

在云雾干扰环境下，目标物体处在云雾环境中，采用发射脉宽为30 ns的脉冲激光雷达，当激光照射到目标表面上时，对接收到的脉冲激光回波信号[11]进行数学模拟，拟合后的图形如图1所示。

由于激光雷达回波波形在受环境干扰因素影响下会发生显著变化，因此，研究激光云雾后向散射回波和无干扰环境[12]下激光的目标回波特征，并与云雾环境中的激光目标回波对比，可以为研究抗云雾干扰及目标识别提供理论依据。

2 基于小波分析的目标识别算法

2.1 算法原理

小波变换[13]是对小波函数ψ(t)作伸缩和平移而产生的一组函数ψa,b(t)。由于二阶样条小波对钟形信号进行卷积后对信号具有光滑作用，因此采用二阶样条小波对回波信号进行处理。其母小波函数为：

(4)

将二阶样条小波ψ2a,b(t)与接收到的脉冲激光雷达回波信号f(t)∈L2(R)作卷积运算，其中平移因子b=0。

(5)

W(t)为计算的卷积信号；ψ2a,b(t)为二阶样条小波函数。其中，卷积信号中包含了回波信号f(t)的峰值和峰宽的信息。

2.2 波峰位置关系

对式(5)进行数学处理得：

(6)

F-1为傅里叶逆变换；F为傅里叶变换。从上文可知，回波信号f(t)建模的表达式为：

(7)

则对式(6)求解可得：

cos[ω(t-ki)]dω

(8)

(9)

当t=ki时，W(t)取得最大值。所以t=ki时，第i个卷积信号和第i个信号的最大值在同一时刻，W(t)的极大值点和f(t)信号的极大值点相对应。因此，二阶样条小波对信号进行卷积运算后，原始信号的峰位置没有改变。

2.3 峰宽的分析

把二阶样条小波母函数ψ2(t)作为函数u(t)的四阶导数，即

ψ2(t)=u‴(t)

(10)

则式(5)可表示为：

(11)

u(t/a)与f(t)作卷积运算后，得到较为光滑的曲线W(t)，可以判断出回波信号中重叠的信号个数以及它们的峰值点。当有多个信号重叠时，通过四阶导数降低各个峰的宽度，从而使原始信号进行分离，确定重叠信号的个数，再由导数峰的峰宽推导出原始信号中的重叠信号峰宽之比。由式(11)可知：平滑信号之后再求四阶导数效果与卷积运算相同，因此，通过重叠信号与二阶样条小波函数的卷积运算可以达到分离重叠信号的目的。

2.4 波峰分辨算子

为了提高对重叠信号的分辨率，使原始信号的重叠信号峰位置与面积保持不变，使用样条函数构造波峰分辨算子，并且使只有比原信号窄的信号才能通过。波峰分辨算子表达式为：

(12)

由于自变量为零时三阶样条小波函数取得最大值，且其函数较为光滑，因此将其作为分辨因子R(t)。重叠信号的个数与分辨因子个数相同，用N表示。分辨因子的峰宽参数为qi，原重叠信号的各个峰宽和分辨因子峰宽成正比。由式(8)可以确定ki，通过卷积运算求到Ni，Ki和σi的比值之后，即可采用分峰表达式对重叠信号进行分离。

3 仿真与结果分析

3.1 参数的选择

针对不同类型和不同重叠程度的信号峰，调整尺度a的大小，用上述方法对其进行处理分析。分析结果表明，由于f(t)与u(t)的卷积起到平滑作用的同时，f(t)的峰宽也会被展宽，即尺度a越大，卷积曲线的峰越宽。由于分离重叠程度较大的信号需要提高分辨率，因此根据离散卷积的定义，要采用尺度小的参数，确保f(t)和卷积信号不被展宽，使得卷积信号峰宽和重叠信号峰宽成正比。由于尺度大小影响卷积运算对信号的平滑效果，尺度越大，平滑效果越强。因此，在选择较小尺度的同时，也要保证得到光滑的卷积曲线。

3.2 对仿真信号的分辨

首先对大量仿真信号进行处理，检验该方法对重叠信号的分离效果。信号的重叠程度用分离度Rs来描述，其中：

(13)

分离度分别为0.25，0.75，0.625的重叠信号，如图2所示，其重叠峰位置各不相同。重叠信号分离前后的对比如表1所示。

以上是对不含噪音的重叠信号的分辨，均采用尺度10。从图2对重叠信号的分离效果可以得知，分离后的峰位置不变，峰宽变窄，重叠信号的基线分离，分辨率得到提高。因此，采用二阶样条小波卷积法对重叠信号的分离非常有效。

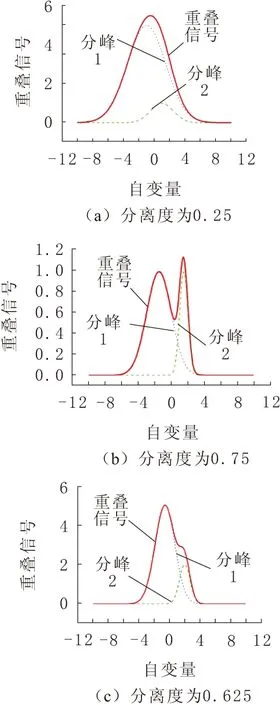
图2 对仿真重叠信号进行分离及效果

从表1可看出，利用上述方法能够成功地从重叠峰信号中分离出独立的子峰，且峰位、峰高的相对误差小于1%。模拟的激光回波信号如图3所示，采用小波卷积法进行分离，经过处理后得到的图形，根据实验经验采用尺度为10。

根据激光的反射理论可知，当激光脉冲穿过云雾照射到目标上时，激光雷达接收器会接收到2个返回脉冲，其中第1个是大气环境对激光的散射，第2个是通过目标物体反射回来的波形。根据上面的算法对激光回波波形进行分辨，激光的后向散射回波如图4a所示，其峰位置在8.3处，目标反射回波如图4b所示，其峰位置在8.5处。由图4可知，后向散射回波的峰值大于目标反射回波的峰值，由激光的反射模型可知，该目标是漫反射物体，返回脉冲宽度也小于激光后向散射脉冲宽度。因此，可将图4a后向散射剔除，保留目标物体的回波作为激光雷达的数据进行处理，从而提高了激光抗云雾干扰的性能。

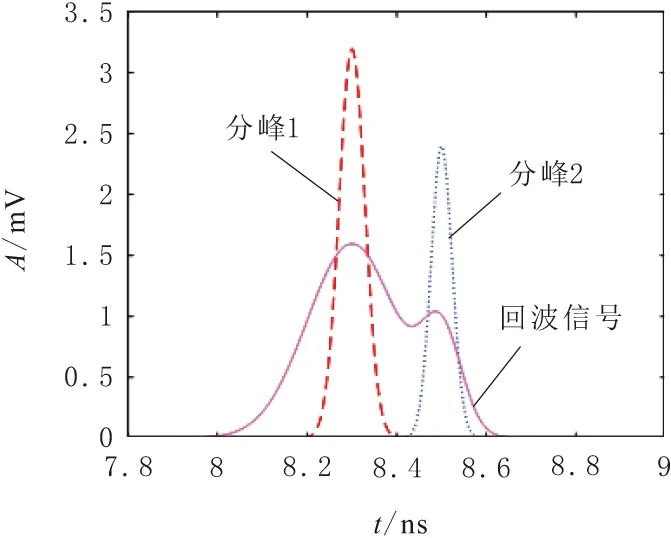
图3 激光回波信号处理情况

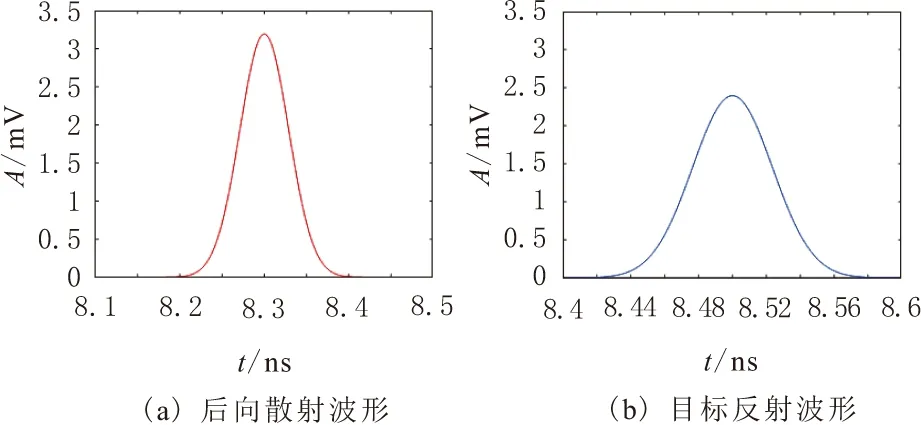
图4 提取后的回波信号

表1 重叠双峰体系处理前后各峰的峰位置、峰值及其误差

4 结束语

根据脉冲激光雷达回波信号特征，进行数学建模，采用小波卷积法对激光雷达回波信号进行分析。仿真证明，该方法能够分离出相互重叠的2个脉冲信号，确定峰值的位置和峰值大小。根据激光后向散射理论，区分激光的后向散射回波和目标信号的反射回波，并将激光后向散射回波剔除，保留目标反射回波作为激光雷达的数据进行处理，从而提高了激光抗云雾干扰的性能，能够有效提高激光雷达抗云雾、雾霾等后向散射干扰。

[1] 吕宏飞,刘丙才.激光在大气中的传输特性研究[J].科技信息,2012(15):53-54,64.

[2] 甘霖,张合,张祥金,等.激光近炸引信单光束脉冲周向探测技术[J].红外与激光工程，2013,42(1):84-89.

[3] Su H T,Liu H W,Shui P L,et al.Adaptive beamforming for nonstationary HF interference cancellation in skywave over-the-horizon radar[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):312-324.

[4] 张京国,高宠,刘建新,等.近距云雾回波蒙特卡罗模拟与实验测量[J].强激光与粒子束,2012,24(12): 2920-2924.

[5] 何佳晶,周晖,刘婷婷,等.一种考虑湿度修正的雾霾检测系统[J].电子测量技术,2015,38(10):96-100.

[6] 隋修武,李瑶,胡秀兵,等.激光粒度分析仪的关键技术及研究进展[J].电子测量与仪器学报,2016,30(10):1449-1459.

[7] 杨雨川,龙超,谭碧涛,等.大气后向散射对主动探测激光脉冲的影响[J].激光与红外,2013,43 (5):482-485.

[8] Yang L M,Wan P, Protopopov V,et al.2μm femtosecond fiber laser at low repetition rate and high pulse energy[J]. Optics Express,2012,20(5):5683-5688.

[9] 杨昭.激光近炸引信的目标探测系统研究[D].吉林:长春理工大学,2012.

[10] 刘诏,张爱武,段乙好,等.全波形机载激光数据分解算法研究[J].高技术通讯,2014,24(2):144-151.

[11] 郭静波,谭博,蔡雄.基于反相双峰指数模型的微弱瞬态极低频信号的估计与检测[J].仪器仪表学报,2015,36(8):1682-1691.

[12] Geng Z, Deng H,Himed B. Adaptive radar beamforming for interference mitigation in radar-wireless spectrum sharing[J].IEEE Signal Processing Letters,2015,22(4):484-488.

[13] 林兆培.基于小波的色谱重叠峰辨识及优化方法研究[D].上海:华东理工大学,2014.