基于元胞遗传算法的多无人机编队集结路径规划

，，， ，

(南京航空航天大学自动化学院，江苏 南京 211106)

0 引言

近年来，无人机被广泛应用于各个领域，并扮演着越来越重要的作用。为了提高无人机执行任务的效率，人们往往会采取多无人机协同编队完成任务的方式，其前提条件之一便是多机集结路径规划[1]。

无人机航迹规划需要满足在自身动力学约束环境下，能够规避威胁区，安全到达任务地点。目前常用的航迹规划算法有A*算法、动态规划算法、神经网络算法、遗传算法、群智能算法等[2]。而对于多机集结路径规划，除了需要满足单机航迹规划需求之外，还需要考虑多机到达时间的协同性以及多机之间的防碰撞[3-5]。

在此，提出了一种基于元胞遗传算法的航迹规划方法[6-9]，保证了全局搜索和局部寻优之间的平衡，更好地保证了种群的多样性。然后针对多机集结路径规划的要求，设计了时间协同和防碰撞策略。最后通过仿真，验证了该算法的有效性和稳定性。

1 单机航迹规划

1.1 航迹编码

对于每一条航迹，都是由一个个航点组成，本文不考虑无人机飞行高度，将航迹规划简化为二维空间内的路径规划，故所涉及到的速度和航程计算都是在二维空间内的投影。记起始点坐标为S(xs,ys)，终点坐标为G(xg,yg)，中间n个航点的坐标为Pi(xi,yi) (i=1, 2, 3, …,n)，则每一条航迹都可以表示为(S,P1,P2,P3, …,Pn,G)的航点序列，为了方便说明，S和G可分别表示为P0(x0,y0)和Pn+1(xn+1,yn+1)。

1.2 适应度函数

适应度函数用于评价航迹的优劣，航迹的适应度越大，说明越满足规划要求。在规划一条航迹时，需要尽可能避开威胁区域，同时为了使油耗最小，航迹应尽可能短。此外，由于多机集结具有时间约束性，所规划的航迹应满足速度约束条件。因此，选取威胁代价、航程代价和速度代价来表示适应度函数。

1.2.1 威胁代价

假设二维空间内有q个威胁点，各威胁点坐标和威胁半径分别为Wj=(xj,yj)，rj(j=1, 2, 3, …,q)。

(1)

图1 威胁代价计算示意

dij为Wj到航线段PiPi+1最短距离，由此可以得出Wj到航线段PiPi+1的威胁代价值：

(2)

则航线段PiPi+1威胁代价值为：

(3)

记整条航迹的威胁代价值为S，则：

(4)

1.2.2 航程代价

在航迹规划过程中，需要使油耗最小，因此整个航程也需要尽量小。对于每条航迹，计算航迹的总长度L，由此可以得出航程代价值：

(5)

1.2.3 速度代价

多无人机集结具有时间约束性，假设所有无人机都需要在T时间内集结完毕，那么对于每架无人机，其飞行速度v应满足：

(6)

为了节省燃油以及应对突发状况，无人机应尽量飞行在巡航速度vc，由此可以得出速度代价值V为：

V=v-vcvmin≤v≤vmax

(7)

综上所述，可以得到航迹的总代价值C为：

C=ksS+klL+kvV

(8)

ks为威胁代价权重系数；kl为航程代价权重系数；kv为速度代价权重系数。使用f表示一个足够大的数，则航迹的适应度函数F可以表示为：

F=f-C

(9)

F值越大，说明规划的航迹越符合要求。

1.3 种群初始化

在进行遗传操作之前，需要先初始化航迹种群。由于航迹是由一个个航点组成的，生成初始航迹也就是生成一系列的航点。采用端点启发初始化的方法来生成初始航点，第i个航点Pi(xi,yi)为：

(10)

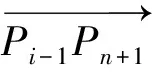
(11)

这样便保证了单个航线段步长不小于起点到终点的最小航线段。

1.4 初始化元胞空间

假设初始种群规模即初始航迹条数为N，建立N=u×w的二维元胞空间，将初始种群随机分布在元胞空间内。采用Moore型邻居结构，元胞空间边界采用周期型边界，如图2所示。在每一个(周期扩展)九宫格内，所有的“☆”都是“★”的邻居，所有的遗传操作都在邻居之间进行。

图2 元胞空间结构

1.5 遗传操作

1.5.1 选择

由于遗传操作只在邻居之间进行，对于每一个中心元胞，只在它的邻居元胞内选择个体遗传到下一代。在此，使用轮盘赌的方式进行个体选择，对于每一个邻居元胞内的个体，分别计算其适应度值Fi，则第i个元胞内的个体被选中的概率psi为：

(12)

1.5.2 交叉

定义交叉概率pc，在[0,1]之间取随机值pcr，若pcr≤pc，则进行交叉操作。

交叉操作如图3所示，进行交叉操作时，对于中心元胞个体Qcen和被选中的邻居元胞个体Qngb，除去初始点和终点，分别选择第c个航点，将其和前一个航点断开，将Qcen的c-1航点和Qngb的c航点相连，将Qngb的c-1航点和Qcen的c航点相连，分别计算新生成的2个航迹适应度，选取适应度大的进入下一代，记为Qnew。

图3 交叉操作

1.5.3 变异

定义变异概率pm，在[0, 1]之间取随机值pmr，若pmr≤pm，则进行变异操作。

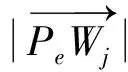
(13)

取其中的最小值hm：

hm=min(h1,h2,h3,…,hq)

(14)

若hm>0，则说明Pe在威胁区外，保留个体Qnew无需变异，否则继续进行变异操作。

如图4所示，假设hm对应的威胁点为W，威胁半径为r，变异之后产生新的航点Pe′(xe′,ye′)，则新航点坐标为：

(15)

ke为取值在[1, 2]之间随机增益系数，ω为随机旋转角度，使得变异具有随机性。变异之后，Pe便跳到了距离Pe长度为ke|hm|的新航点Pe′上，由于变异具有随机性，因此变异之后Pe′可能依旧在威胁区内。

图4 变异操作

在变异操作之后，更新Qnew为新的个体，仍然命名为Qnew，计算Qnew的适应度Fnew，并与中心元胞个体Qcen的适应度Fcen进行比较，若Fnew>Fcen，则替换中心元胞个体为Qnew，否则放弃新个体。

1.6 算法终止条件

由于算法计算量大，一般很难在短时间内找到全局最优解，因此可以设置以下终止条件以节省计算时间：

a. 设置较为合适的适应度标准F0，一旦新个体中有适应度值不小于F0的出现，则终止寻优，选择该个体作为最终航迹。

b. 设置最大进化次数K，一旦进化次数达到K次，则终止寻优，选取其中适应度值最大的个体作为最终航迹。

同时设置以上2个条件，可以得到相对满足条件的“次优解”。

1.7 航迹平滑处理

由于无人机飞行性能的约束，它的最小转弯角必须大于某个阈值φm，由上述算法生成的最终航迹可能存在大量角度小于φm的尖角，不满足无人机转向要求，因此需要对这些尖角进行平滑处理。

对于航迹上需要进行平滑处理的航点Pi，若Pi-1和Pi+1的连线不经过威胁区，如图5a所示。则将Pi移至航线段的中点Pi′处。若Pi-1和Pi+1的连线经过威胁区，如图5b所示，则分别在PiPi-1和PiPi+1的1/M处取点Pi1和Pi2，连接Pi1Pi2，组成新的航迹。

图5 航迹平滑处理

2 多机协同规划

多机协同飞行主要需要考虑同时到达目标点和飞行过程中的防碰撞。对于可以相互通信的无人机而言，只需相互之间实时汇报自己的状态，再通过速度调整即可。对于通信无法正常建立的情况下，可由下文提出的策略进行调整。

2.1 时间协同

多无人机编队集结需要多架无人机在规定时间内到达指定集结地点，最简单的方法就是进行速度控制。对于第k架无人机，其初始飞行速度vk0为：

(16)

Lk为第k架无人机的总航程，T为集结时间。由于无人机飞途中会有各种不确定性，无法保证全程都是按照设定速度飞行，由此提出了速度调整策略。

扩展第k架无人机航迹的航点编码Pki(xki,yki)，增加到达第i个航点的约定时间tki，其值为：

(17)

Lki为无人机飞到Pki时的总航程。这样得到新的航点编码Pki(xki,yki,tki)。无人机飞行到Pki时，根据已飞时间tk和飞到下一航点的约定时间tk(i+1)，可以确定下一阶段的飞行速度vk：

(18)

通过不断地对速度进行微调，便可以基本保证在约定时间到达对应航点，直至到达终点。

2.2 防碰撞策略

由于每架无人机都是单独进行航迹规划，因此规划出的航迹之间可能存在交叉或距离过近的情况，可能导致无人机之间发生碰撞，因此需要进行无人机之间防碰撞设计。

本文是在简化的二维空间内进行的航迹规划，而无人机实际飞行在三维空间内，因此，对于航迹有交叉或者距离小于安全距离Ds的无人机，可使其飞行在不同的高度层，每层之间相差至少1个安全距离。为了平衡燃油消耗，二维空间内航程大的无人机应飞行在较低的高度。这样，即使航迹有交叉或距离过近，也不会发生碰撞事故。

3 仿真验证

为验证本算法的有效性，设计了仿真验证环节，约束条件如下所述：

a. 待集结的无人机为3架，分别为UAV1，UAV2和UAV3。

b. 各无人机的起点分别为S1(10, 10)，S2(20, 0)，S3(0, 30)，终点为G(100, 100)，单位为 km。

c. 设置6个威胁区域，威胁中心和威胁半径分别为：W1(15, 88)，r1=10；W2(23, 50),r2=15；W3(25, 15),r3=10；W4(57, 10),r4=10；W5(23, 50),r5=15；W6(55, 75),r6=20。

d. 无人机最小转弯角φm=60°，最小速度vmin=40 km/h，最大速度vmax=200 km/h，巡航速度vc=140 km/h，安全距离Ds=80 m。

e. 集结时间T=60 min。

设置每条航迹的航点数为9，初始种群大小(即航迹数)为40，分布在5×8的元胞空间内，进化代数为50。仿真结果如图6所示。

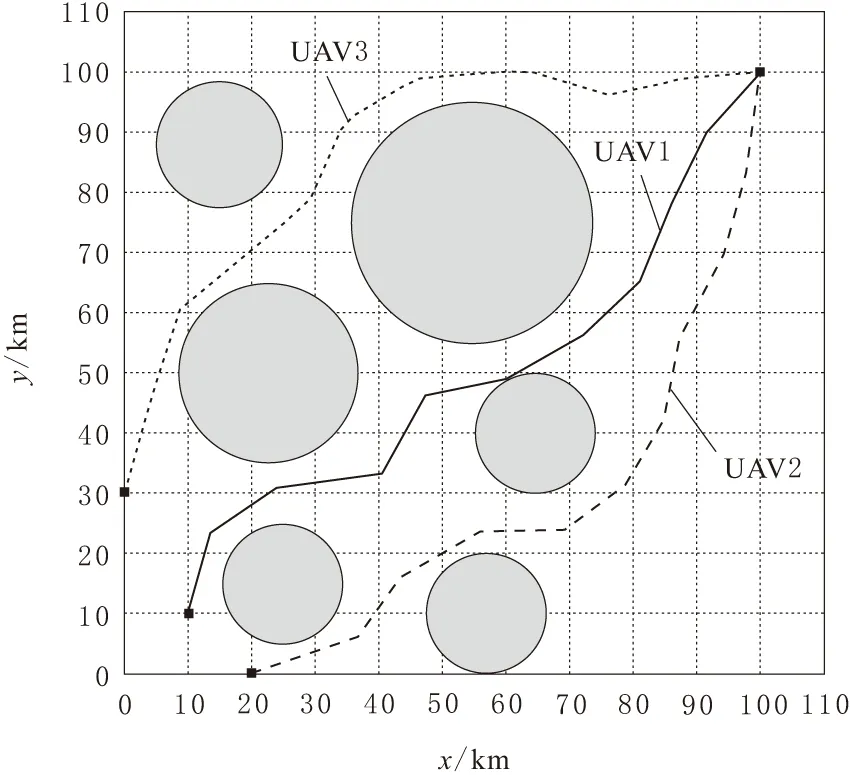
图6 三无人机协同航迹规划

根据仿真数据，计算各无人机的初始速度分别为v10=137.69 km/h，v20=142.49 km/h,v10=141.84 km/h，基本接近巡航速度vc，满足规划要求，由此可以计算出无人机到达各航点的预定时间，部分航点数据如表1所示。

表1 部分航点数据

仿真结果表明，规划出的航迹能很好地规避威胁区，并且满足航程和速度约束。

4 结束语

采用元胞遗传算法对多无人机协同编队的集结路径进行了规划，保证了全局搜索和局部寻优之间的平衡，使得初始种群(航迹)能够更好地保持其多样性。针对多机协同航迹规划的时间约束，在适应度函数中加入了基于时间约束的速度代价，使得规划出的航迹满足无人机在较大的范围内实时调整速度的要求，以便各无人机能够在突发状况下依旧能够准时到达集结点。针对多机防碰撞问题，设计了基于高度差的规划策略。最终仿真结果表明，规划出的航迹满足各项基本要求，算法搜索成功率高，具备良好的稳定性。

[1] 樊琼剑, 杨忠, 方挺, 等. 多无人机协同编队飞行控制的研究现状[J]. 航空学报, 2009, 30(4): 683-691.

[2] 陈江涛, 王文光, 孙进平. 基于改进遗传算法的无人机航迹规划[J]. 计算机工程与应用, 2016, 52(增刊1): 11-15.

[3] 倪良巧, 王道波, 蒋婉玥. 时间协同多无人机编队航迹规划[J]. 机械与电子, 2016, 34(2): 7-11.

[4] 周青, 张锐, 索晓杰, 等. 具有时间约束的无人机遗传算法航迹规划[J]. 航空计算技术, 2016, 46(2): 93-96, 101.

[5] Cetin O, Yilmaz G. Real-time autonomous UAV formation flight with collision and obstacle avoidance in unknown environment[J]. Journal of Intelligent & Robotic Systems, 2016, 84(1/2/3/4): 1-19.

[6] 林志龙, 鲁宇明. 元胞遗传算法的多样性研究[J].电子科技, 2015, 28(4): 9-12.

[7] Zhang Y, Wan X Y, Zheng X D,et al. Cellular genetic algorithm for multiobjective optimization based on orthogonal design[J]. Acta Electronica Sinica, 2016, 23(10): 4742-4746.

[8] Canyurt O E, Hajela P. Cellular genetic algorithm technique for the multicriterion design optimization[J]. Structural & Multidisciplinary Optimization, 2010, 40(1/2/3/4/5/6): 201-214.

[9] 张屹, 刘铮, 胡方军, 等. 基于元胞遗传算法的移动机器人路径规划[J]. 机床与液压, 2014, 42(9): 17-20.