方钢管混凝土柱−钢梁外环板式节点抗剪性能

别雪梦，李召，管文强，杜国锋



方钢管混凝土柱−钢梁外环板式节点抗剪性能

别雪梦，李召，管文强，杜国锋

(1. 长江大学城市建设学院，湖北 荆州，434023；2. 长江大学 结构工程与防灾研究所，湖北 荆州，434023)

为研究方钢管混凝土柱−钢梁外环板式节点抗剪性能,以钢管混凝土柱节点试验尺寸为参照，建立方钢管混凝土柱−钢梁外环板式节点在往复荷载作用下的精细有限元分析模型。该模型考虑材料非线性、混凝土材料在循环荷载下的损伤退化、钢和混凝土之间的相互作用等因素的影响。通过与试验结果进行对比分析，验证该有限元模型具有较好的精度和可靠性。此后研究柱宽厚比、核心混凝土强度、轴压比和节点核心区高宽比等因素对节点的影响，提出一种方钢管混凝土柱−钢梁外环板式节点的核心区剪力−剪切变形恢复力模型。研究结果表明，该模型具有实用性，可为工程设计提供实际依据。

方钢管混凝土柱−钢梁外环板式节点；有限元分析；钢筋混凝土楼板；抗剪性能

方钢管混凝土柱与钢梁的刚性连接常采用外环板式节点。外环板节点具有传力明确、节点区应力分布较均匀、塑性性能好、刚度大和承载力高等优点。目前国内外学者对方钢管混凝土柱外加强环式节点研究较少[1−6]，且节点破坏模式大部分为梁铰破坏或节点弯曲破坏，节点剪切破坏模式相对较少。此外对楼板影响下的方钢管混凝土柱−钢梁外环板式节点核心区抗剪承载力计算公式以及剪力−剪切变形恢复力模型的研究报道较少。但实际工程中由于楼板的存在导致节点极易发生剪切破坏。因此，本文作者以文献[7]中的方钢管混凝土柱−钢梁外环板式节点(以下简称“节点”)为参照，建立考虑材料损伤的节点精细化有限元分析(FEA)模型，对节点在往复荷载作用下的破坏形态和全过程进行分析，并与试验结果进行对比来验证该有限元模型的有效性，且在此基础上对节点进行参数分析。最后基于参数分析结果，提出该类节点的恢复力模型，研究结果可为日后节点抗震计算分析提供有益参考。

1 钢管混凝土柱−钢梁节点有限元模型

1.1 有限元模型的建立

1.1.1 材料的本构模型

钢材的本构关系采用文献[7]推荐的三折线模型，在有限元软件中采用塑性模型来描述这一关系。节点涉及钢管内的核心混凝土和楼板中的普通混凝土，核心混凝土和普通混凝土受压应力−应变关系分别采用应用较广的刘威[8]的核心混凝土本构模型和过镇海[9]的混凝土本构模型，并根据文献[10]定义了2种弹性模量分别为2.66×104N/mm2和2.8×104N/mm2；2种混凝土受拉应力−应变关系采用GB 50010—2010“混凝土结构设计规范”[11]推荐的混凝土受拉本构模型。在有限元软件ABAQUS 中混凝土的本构关系通过混凝土损伤塑性模型(简称CDP)中输入混凝土的受压和受拉应力−应变关系来反映，该模型通过受拉损伤因子t和受压损伤因子c(0≤t,c≤1)来反映其刚度退化。CDP 模型中损伤变量计算式为

1.1.2 单元、网格和边界条件

核心混凝土、楼板混凝土、钢管、钢梁以及加载板均采用八节点减缩积分实体单元，钢筋采用两节点的三维线性梁单元。单元网格划分采用结构化划分网格技术，并在保证计算精确度的同时对网格进行调整来提高计算效率；在靠近节点核心区部位进行网格加密(见图1)。对柱顶对称中线的，方向平动及，方向转动进行约束；对柱底对称中线，，方向平动及，方向转动进行约束；同时对梁端，方向转动进行限制。在柱顶按轴压比以集中力方式施加轴向力；在梁加载端以位移加载方式施加单向荷载或往复荷载(见图1)。

图1 外环板式节点CFRTJ-4有限元模型

1.1.3 接触和连接处理

CFST柱的核心混凝土与钢管之间的接触面存在切向作用和法向作用。其切向采用库仑摩擦模型来传递剪应力，摩擦因数根据刘威[8]的建议取0.25；法向采用硬接触。钢梁和柱，以及钢梁和楼板之间均采用绑定约束来进行模拟。钢筋和楼板混凝土之间采用分离式模型中将钢筋内置于楼板混凝土中的方式来进行分析。

本文所建立的模型考虑了钢和混凝土的材料非线性、混凝土损伤塑性、由接触、滑移等引起的边界条件非线性问题，最终归结于求解非线性平衡方程组。

1.2 有限元模型的验证

为验证上文提及的材料本构模型、单元类型、边界条件和接触等设置在节点受力分析中的适用性，本文利用该有限元模型对文献[7]中带楼板钢管混凝土柱−钢梁外环板式节点CFRTJ-4进行分析，并与试验结果进行对比。节点CFRTJ-4的材料性能参数见表1和表2，截面尺寸见图2。其中：柱中核心混凝土和楼板中普通混凝土强度等级分别为C40和C35；柱的钢管壁厚=8 mm；钢梁下翼缘钢板厚8 mm，其他为6 mm；柱轴压比=0.3，柱总高=1 396 mm，节点核心区高度=291 mm、宽度(即柱宽)=250 mm。

表1 钢材的材料性能

表2 混凝土的材料性能

1.2.1 在单向荷载作用下节点的数值模拟

节点 CFRTJ-4在单向加载下的梁端荷载−位移(−)计算曲线和核心区剪力−剪切变形(–)计算曲线与试验骨架曲线进行比较分别见图3(a)和图3(b)。由图3可见：计算曲线与试验曲线趋势相近，节点的剪切刚度基本相同。在试验中由于柱翼缘、腹板拼接焊缝发生破坏，使得曲线出现下降段，剪切破坏并没有完全形成，而有限元模型较好地模拟了剪切破坏过程，梁端没有发生局部屈服，因此骨架曲线也没有明显的下降段。

单位：mm

(a) P−Δ曲线；(b) V– γ曲线

节点CFRTJ-4在单向加载下的钢管和核心混凝土Mises应力图分别见图4(a)和图4(b)。由图4可见：节点破坏时，部分外环板、钢管、钢梁翼缘进入屈服状态；钢梁根部和柱角存在应力集中，核心混凝土被压碎；节点剪切破坏及外环板拉断是节点最终破坏缘由。节点破坏形态与试验现象相符，说明建立的有限元模型可行性较好。

1.2.2 在循环往复荷载作用下节点的数值模拟

节点CFRTJ-4在循环往复荷载下的−计算曲线和–计算曲线与试验骨架曲线进行比较分别见图5(a)和图5(b)。由图5可见：节点滞回曲线较饱满，没有明显的捏缩现象；节点塑性变形能力较强，具有很好的抗震性能和耗能能力。计算曲线与试验曲线吻合较好，说明建立的有限元模型精度较高。

(a) 节点钢管；(b) 节点核心混凝土

(a) P−Δ曲线；(b) V– γ曲线

节点CFRTJ-4在循环往复荷载下的钢管和核心混凝土Mises应力图分别见图6(a)和图6(b)。由图6可见：节点的破坏区域在靠近节点的梁根部位置；钢梁根部和柱角存在应力集中；节点的钢梁、外钢管进入了屈服状态，核心混凝土被压碎；节点破坏形态与试验结果相符，说明建立的有限元模型可行性较好。

(a) 节点钢管；(b) 节点核心混凝土

2 参数分析

为深入研究节点抗剪性能，本文基于上文模拟较准确的节点CFRTJ-4有限元模型，对节点进行参数分析，为节点实用计算方法和简化模型的研究奠定基础。主要参数包括柱的宽厚比()、核心混凝土强度(cu)、柱轴压比()及核心区高宽比()等，试件参数见表3。表3中：为柱宽，250 mm；宽厚比()通过改变柱的钢管壁厚()来分析；高宽比()为节点核心区高度()和宽度()的比值，通过改变核心区的高度()来实现；在对高宽比()进行参数分析时，只选取当轴压比()为0时，不同高宽比(=0.70，1.16和1.94)对节点受力的影响。此表中的CF-G1-1，CF-G1-2，CF-G1-3，CF-G2-1，CF-G2-2和CF-G2-3为后面提出恢复力模型时所用节点。

2.1 宽厚比(B/t)

不同宽厚比()下节点核心区剪力−剪切变形关系(j–j)的计算结果见图7(a)。由图7(a)可见：宽厚比()对核心区j–j曲线的影响较为明显；节点抗剪承载力和强化阶段的刚度随着宽厚比增大而增大。

表3 试件参数

注：CFRTJ-4为试验节点，其他节点为有限元分析节点

2.2 核心混凝土强度(fcu)

不同核心混凝土强度(cu)下节点核心区j–j的计算结果见图7(b)。由图7(b)可见：cu对核心区j–j关系有一定影响，对核心区抗剪刚度的影响不很明显；核心区抗剪承载力随着cu的提高而增大。

(a) 宽厚比B/t；(b) 核心混凝土强度fcu；(c) 轴压比n；(d) 高宽比h/B

2.3 轴压比(n)

不同轴压比()下节点核心区j–j的计算结果见图7(c)。由图7(c)可见：对试件抗剪承载力有一定影响，对弹性阶段刚度影响很小；当＜0.5时，核心区抗剪承载力随着的增大，有一定程度的提高；但当＞0.5时，抗剪承载力随着的增大而降低；当从0.6变为0.8时，节点破坏模式从节点域剪切破坏变为柱压弯破坏。

2.4 高宽比(h/B)

不同高宽比()下节点核心区j–j的计算结果见图7(d)。由图7(d)可见：对核心区的抗剪承载力影响较明显，对曲线弹性阶段刚度的影响较明显；核心区抗剪承载力随着的提高有所降低。

3 节点的恢复力模型

3.1 核心区剪力−剪切变形恢复力模型

节点恢复力模型是节点整体或组成部分在往复荷载下的力−变形关系，是进行节点弹塑性地震全过程分析的重要前提。叠加钢管和混凝土的j–j关系来求得核心区整体的j–j关系，是研究核心区j–j曲线的主要方法[13−18]。通常认为，方钢管混凝土柱−钢梁外环板式节点抗剪承载力主要由节点核心区混凝土、钢管腹板以及钢板框架(由钢管翼缘与外环板组成)共同提供。但是通过研究结果表明，钢板框架对节点抗剪承载力的贡献很小，因此本文不进行讨论。节点抗剪承载力主要由钢管腹板和核心区混凝土(分别以平面抗剪和斜压杆模式对抗剪做出贡献)共同承担。本文所研究节点核心区剪力−剪变(j–j)的下降段并不明显，因为节点在达到极限承载力后，核心混凝土分担的剪力下降，但钢管仍处于强化段，整体的剪力可能还呈上升趋势。因此，本文作者认为钢管混凝土柱−钢梁外环板式节点核心区j–j骨架线可采用图8的三折线模型，总剪力在达到u后保持不变，模型有弹性段刚度(el)、抗剪屈服承载力(y)、抗剪极限承载力(u)及此时的极限剪切变形(u)共4个参数。

图8 节点核心区剪力(Vj)−剪切变形(γj)关系

3.1.1 弹性阶段刚度(el)

研究结果表明：加载初期，钢管对核心混凝土的约束较小，外钢管和核心混凝土的变形基本协调。因此核心区整体剪切刚度(el)可视为钢管刚度(el,s)和混凝土刚度(el,c)的叠加。钢管的弹性剪切刚度(el,s)为

式中：s为钢材剪切模量，根据规范[19]，s=7.9×104N/mm2；vy,p为钢管屈服时其受剪面积，根据FUKUMOTO等[15]的研究，vy,p=s,p/2，s,p为方钢管横截面积，mm2。钢管屈服时的剪切变形(y,wp)为

钢管屈服可以看做节点核心区屈服[15]。当节点核心区屈服时，混凝土的弹性剪切刚度(el,c)为

式中：c,y表示变形为y,wp时混凝土承担的剪力。参数分析表明：轴压比()对节点核心区弹性阶段刚度影响很小，混凝土的弹性剪切刚度(el,c)主要与宽厚比()、核心混凝土强度(cu)和高宽比()有关。引入韩林海[18]定义的约束效应系数(p)来表示宽厚比()和核心混凝土强度(cu)对核心区性能的影响。

图9(a)所示为c,yFEA/(c,pc,p)与p的关系图。图中，c,yFEA表示核心区剪切变形为y,wp时混凝土的剪力；c,p和c,p分别为核心区混凝土的抗压强度和核心混凝土横截面积。为消除对el,c的影响，算例的为1.16。由图9(a)可见：c,yFEA/(c,pc,p)和p的关系可表示为c,yFEA/(c,pc,p)=0.016+0028p。图9(b)所示为c,yFEA/c,yFEA1.16与的关系图。图中，c,yFEA1.16表示核心区剪切变形为y,wp时，核心区高宽比()为1.16的混凝土的剪力。由图9(b)可见：c,yFEA/c,yFEA1.16和的关系可表示为c,yFEA/c,yFEA1.16=1.7−0.5。总结约束效应系数(p)和高宽比()的影响，c,y=(0.016+0028p)(1.7−0.5)c,pc,p，从而可得到el,c的表达式为

因此，根据叠加原理节点核心区整体弹性剪切刚度(el)为

3.1.2 抗剪极限承载力(u)

节点核心区抗剪极限承载力(u)可看做钢管极限承载力(s,u)和混凝土极限承载力(c,u)的叠加。其中混凝土承载力(c,u)通过叠加混凝土平面抗剪承载力(c,u1)和斜压杆模式抗剪承载力(c,u2)得到。通过参数分析表明：宽厚比()、核心混凝土强度(cu)、轴压比()和高宽比()对核心区抗剪极限承载力(u)影响较大。

总结约束效应系数(p)、高宽比()和轴压比()的影响，s,u的表达式为

2)混凝土极限承载力(c,u)。混凝土承载力(c,u)通过叠加混凝土平面抗剪承载力(c,u1)和斜压杆模式抗剪承载力(c,u2)得到。首先分析平面抗剪承载力(c,u1)。图11(a)所示为c,uFEA/c,f与p的关系图。图中，c,uFEA为在极限点时计算的混凝土剪力；c,f为混凝土剪力参考值，c,f=0.3c,pc,p。算例的为0，为1.16。由图11(a)可见：c,uFEA/c,f和p的关系可表示为c,uFEA/c,f= 0.15+0.1p。图11(b) 所示为c,uFEA/c,uFEA1.16与的关系图。图中，c,uFEA1.16表示核心区高宽比()为1.16，在极限点时计算的混凝土剪力。算例的为0。由图11(b)可见：c,uFEA/c,uFEA1.16和的关系可表示为c,uFEA/c,uFEA1.16=1.3−0.22。图11(c)所示为c,uFEA/c,uFEAn0与的关系图。图中，c,uFEAn0表示轴压比()为0，在极限点时计算的混凝土剪力。由图11(c)可见：c,uFEA/c,uFEAn0和的关系可表示为c,uFEA/c,uFEAn0= 1+0.35。总结约束效应系数(p)、高宽比()和轴压比()的影响，c,u1的表达式为

(a)s,uFEA/s,f−p；(b)s,uFEA/s,uFEA1.16−；(c)s,uFEA/s,uFEAn0−

图10s,uFEA/s,f−p，s,uFEA/s,uFEA1.16−和s,uFEA/s,uFEAn0−关系

Fig. 10 Relations ofs,uFEA/s,f−p，s,uFEA/s,uFEA1.16−ands,uFEA/s,uFEAn0−

(a) Vc,uFEA/Vc,f −ξp；(b) Vc,uFEA /Vc,uFEA1.16−h/B；(c) Vc,uFEA/Vc,uFEAn0−n

c,c为圆柱体抗压强度，N/mm2。总结核心混凝土平面抗剪承载力(c,u1)和斜压杆抗剪承载力(c,u2)可以得到混凝土抗剪极限承载力(c,u)为

因此，根据叠加原理方钢管混凝土柱−钢梁外环板式节点核心区抗剪极限承载力(u)为

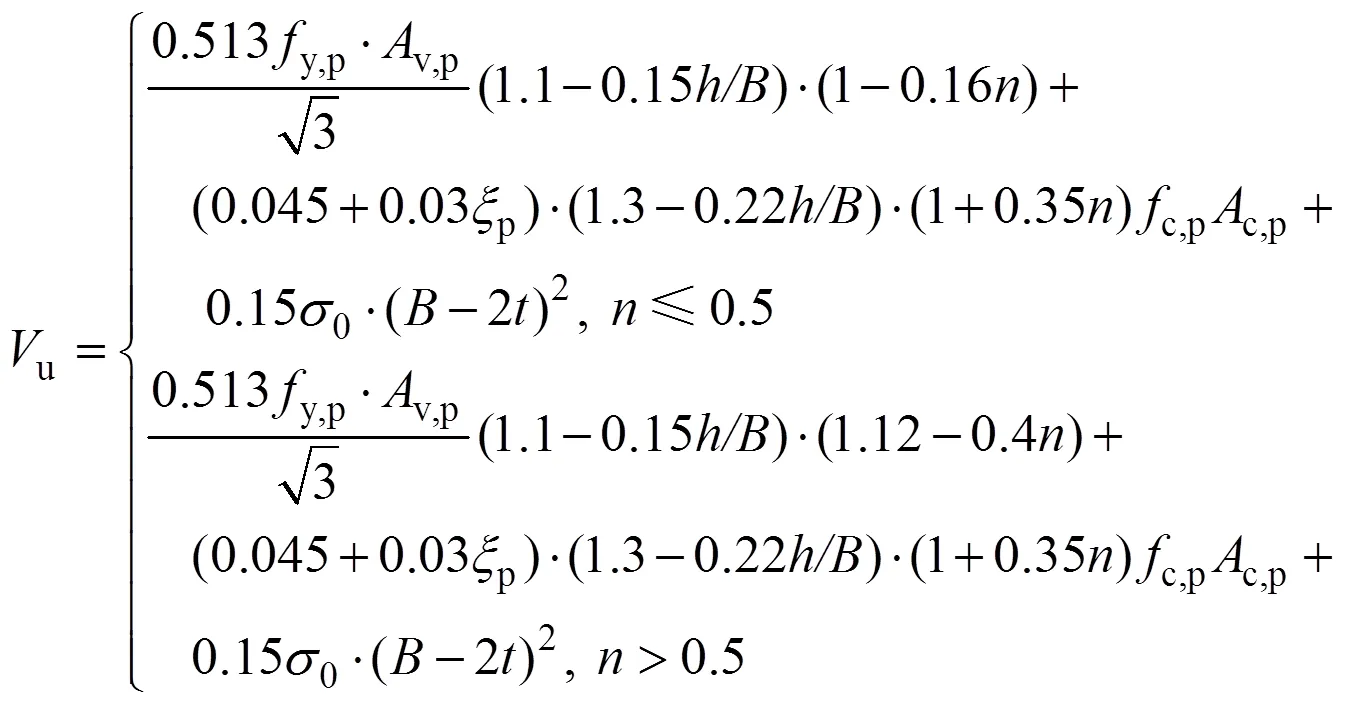
3.1.3 抗剪屈服承载力(y)

根据计算结果和试验结果可知：核心区的抗剪屈服承载力(y)和抗剪极限承载力(u)关系为

y=0.68u(12)

假设钢管与核心混凝土变形协调，核心区节点域的变形图如图12所示。图中：c和t分别为平面压缩应变和平面拉伸应变；ε和ε分别为向和向应变；γ为剪切应变；为核心区对角线和水平面的夹角。c，t和γ计算表达式分别为：

设tc=−t/c，联立方程组可得剪切应变(γ)为

当混凝土的压缩应变(c)取核心混凝土峰值压应变值(0)[18]见式(14)，可得到核心区极限剪切变形(u)见式(15)。

图12 节点域变形状态

为了确定u，首先得求出tc。本文研究tc与约束效应系数(p)，uu,1.16与高宽比()及uu,n0与轴压比()的关系分别如图13(a)~(c)所示。由图13(a)可见：tc与p成比例关系，tc=1.7。由图13(b)可见：uu,1.16与成线性关系，uu,1.16=0.837+0.05。由图13(c)可见：uu,n0与呈线性关系，uu,n0=1−0.1。因此，极限剪切变形(u)为

本文所提公式的应用范围如下：y,p为393~526 N/mm2，c,p为22~49 N/mm2，为6~12 mm，p为1.5~3.4，为0~0.8，为0.7~2.0。

(a) ktc−ξp；(b) γu/γu,1.16−h/B；(c) γu/γu,n0−n

方钢管混凝土柱−钢梁节点剪力−剪切变形曲线的恢复力模型可选用平顶退化三线型模型如图14所示，其骨架线可按图8确定，弹性阶段按弹性刚度加、卸载，弹塑性阶段按骨架线进行加载。如从1点或3点卸载时，卸载轨迹可近似取斜直线，按弹性刚度进行卸载。卸载至反向2点或4点再加载，2点或4点纵坐标为1点和3点的0.3倍。再加载线为斜直线，目标点为上一循环的卸载点。若为第1次反向加载，则目标点为骨架线上的屈服点。

图14 核心区剪力−剪变恢复力模型

3.2 恢复力模型的验证

为验证本文提出带楼板的方钢管混凝土柱−钢梁外环板式节点核心区剪力−剪切变形恢复力模型的合理性，将试验结果和有限元模拟结果与其进行对比，结果见图15。由图15可见：忽略有限元模拟结果中由损伤导致的节点刚度退化外，恢复力模型的弹性阶段刚度、承载力等与模拟结果和试验结果吻合较好。

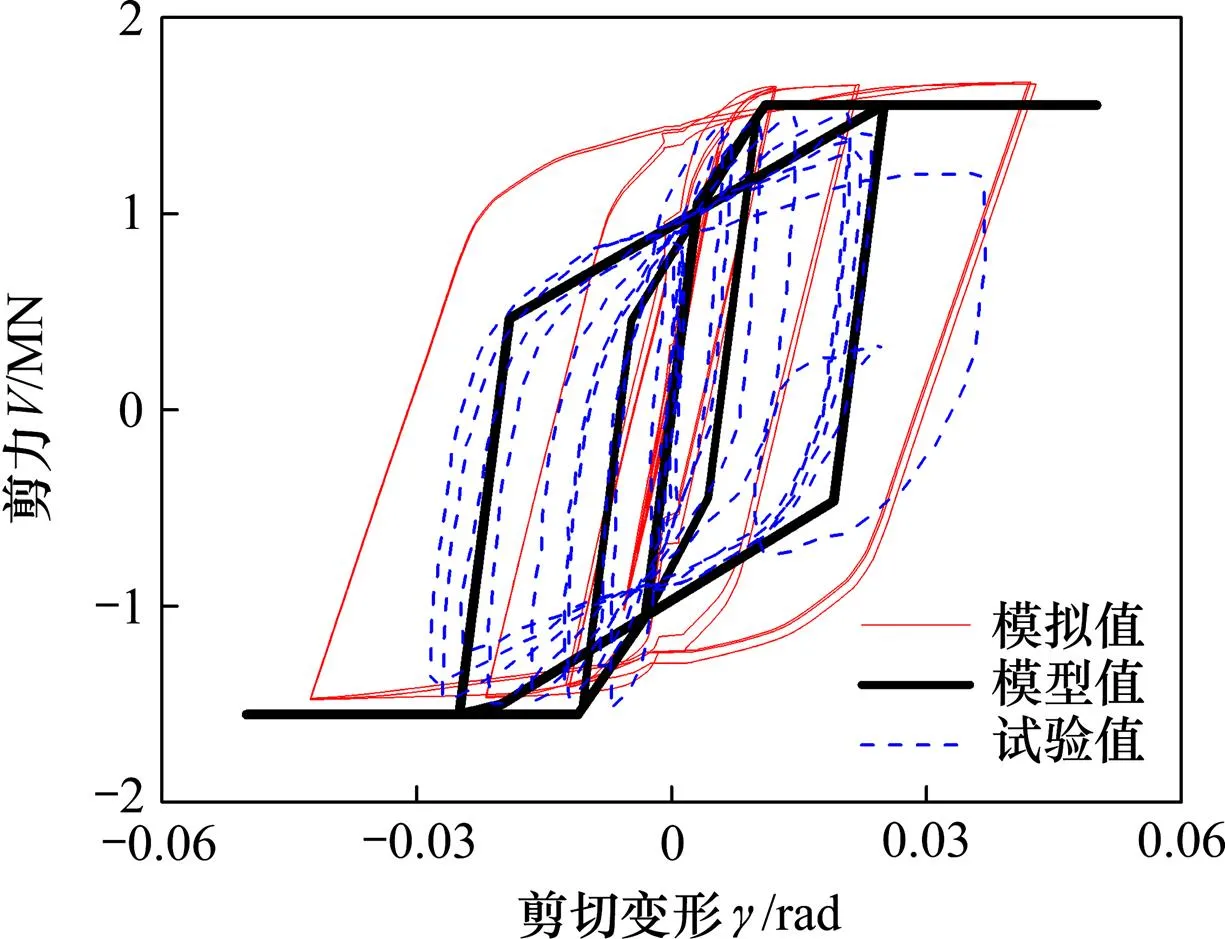
图15 CFRTJ-4核心区剪力−剪切变形模型、有限元计算结果和试验结果的比较

4 结论

1) 考虑材料非线性、混凝土的损伤退化、钢管和核心混凝土间的接触等因素，建立了带楼板的钢管混凝土柱−钢梁外环板式节点精细有限元模型。

2) 获得了柱宽厚比、核心混凝土强度、柱轴压比以及节点核心区高宽比等参数对节点抗剪承载力的影响规律，提出节点抗剪承载力计算公式。

3) 提出考虑楼板影响的方钢管混凝土柱−钢梁外环板式节点的核心区剪力−剪切变形恢复力模型。

[1] 李志南. 带楼板钢管混凝土环梁节点的试验研究和有限元分析[D]. 长沙: 中南大学土木工程学院, 2008: 1−79. LI Zhinan. Finite element analysis and experimental research of CFST connections with exterior diaphragms considering floor slab[D]. Changsha: Central South University. School of Civil Engineering, 2008: 1−79.

[2] 别雪梦, 李召, 管文强, 等. 带楼板的外加强环式 CFST 节点非线性数值模拟[J]. 工业建筑, 2016, 46(10): 163−168. BIE Xuemeng, LI Zhao, GUAN Wenqiang, et al. Nonlinear numerical simulation on the behavior of CFST connections with exterior diaphragms considering floor slab[J]. Industrial Construction, 2016, 46(10): 163−168.

[3] 王文达, 秦庚, 张鹏鹏. 钢管混凝土柱−钢梁外环板节点抗弯承载力计算方法[J]. 土木建筑与环境工程, 2011, 33(4): 29−34. WANG Wenda, QIN Geng, ZHANG Pengpeng. Design approach on flexural load-carrying capacity of steel beam to CFST column joints with external stiffening ring[J]. Journal of Civil, Architectural and Environmental Engineering, 2011, 33(4): 29−34.

[4] 黄炳生, 杜培源, 黄顾忠. 方钢管混凝土柱−钢梁外隔板节点拟静力试验研究[J]. 土木工程学报, 2012, 45(5): 50−57. HUANG Bingsheng, DU Peiyuan, HUANG Guzhong. Quasi-static experimental study of outer diaphragm connections between square concrete filled steel tube columns and steel beams[J]. China Civil Engineering Journal, 2012, 45(5): 50−57.

[5] LI X, XIAO Y, WU Y T. Seismic behavior of exterior connections with steel beams bolted to CFT columns[J]. Journal of Constructional Steel Research, 2009, 65(7): 1438−1446.

[6] QUAN C, WANG W, ZHOU J, et al. Cyclic behavior of stiffened joints between concrete-filled steel tubular column and steel beam with narrow outer diaphragm and partial joint penetration welds[J]. Frontiers of Structural and Civil Engineering, 2016, 10(3): 333−344.

[7] 聂建国, 秦凯, 肖岩. 方钢管混凝土柱节点的试验研究及非线性有限元分析[J]. 工程力学, 2006, 23(11): 99−115. NIE Jianguo, QIN kai, XIAO Yan. Experimental investigation and nonlinear finite element analysis on the behavior of concrete-filled square steel tubular column connections[J]. Engineering Mechanics, 2006, 23(11): 99−115.

[8] 刘威. 钢管混凝土局部受压时的工作机理研究[D]. 福州: 福州大学土木工程学院, 2005: 1−158. LIU Wei. Research on mechanism of concrete-filled steel tubes subjected to local compression[D]. Fuzhou: Fuzhou University. College of Civil Engineering, 2005: 1−158.

[9] 过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 2013: 1−22. GUO Zhenhai. Principles of reinforced concrete[M]. Beijing: Tsinghua University Press, 2013: 1−22.

[10] ACI Committee 318. Building code requirements for structural concrete and commentary[M]. Detroit, USA: American Concrete Institute, 2014: 1−5.

[11] GB 50010—2010, 混凝土结构设计规范[S]. GB 50010—2010, Code for Design of Concrete Structures[S].

[12] ABAQUS Inc. ABAQUS analysis theory manual[M]. Rhale Island: ABAQUS Inc, 2016: 1−841.

[13] NISHIYAMA I, FUJIMOTO T, FUKUMOTO T, et al. Inelastic force-deformation response of joint shear panels in beam-column moment connections to concrete-filled tubes[J]. Journal of Structural Engineering, 2004, 130(2): 244−252.

[14] CHENG C T, CHUNG L L. Seismic performance of steel beams to concrete-filled steel tubular column connections[J]. Journal of Constructional Steel Research, 2003, 59(3): 405−426.

[15] FUKUMOTO T, MORITA K. Elastoplastic behavior of panel zone in steel beam-to-concrete filled steel tube column moment connections[J]. Journal of Structural Engineering, ASCE, 2005, 131(12): 1841−1853.

[16] 李威. 圆钢管混凝土柱−钢梁外环板式框架节点抗震性能研究[D]. 北京: 清华大学土木工程系, 2011: 1−159. LI Wei. Study on the seismic performance of circular concrete- filled steel tubular column to steel beam joint with external diaphragm[D]. Beijing: Tsinghua University. Department of Civil Engineering, 2011: 1−159.

[17] 秦凯. 方钢管混凝土柱与钢−混凝土组合梁连接节点的性能研究[D]. 北京: 清华大学土木工程系, 2006: 1−158. QIN Kai. Study on the performance of concrete filled square steel tubular column-steel concrete composite beam[D]. Beijing: Tsinghua University. Department of Civil Engineering, 2006: 1−158.

[18] 韩林海. 钢管混凝土结构-理论与实践[M]. 2版. 北京: 科学出版社, 2007: 1−755. HAN Linhai. Concrete filled steel tube structure- theory and practice[M]. 2nd ed. Beijing: Science Press, 2007: 1−755.

[19] GB 50017—2003, 钢结构设计规范[S]. GB 50017—2003, Code for design of steel structures[S].

[20] 唐九如. 钢筋混凝土框架节点抗震[M]. 南京: 东南大学出版社, 1989: 1−544. TANG Jiuru. Seismic resistance of joints in reinforced concrete frames[M]. Nanjing: Southeast University Press, 1989: 1−544.

[21] PARRA-MONTESINOS G, WIGHT J K. Modeling shear behavior of hybrid RCS beam-column connections[J]. Journal of Structural Engineering, 2001, 127(1): 3−11.

(编辑 杨幼平)

Shear performance of square concrete-filled steel tubular column to steel beam joint with external diaphragm

BIE Xuemeng, LI Zhao, GUAN Wenqiang, DU Guofeng

(1. School of Urban Construction, Yangtze University, Jingzhou 434023, China; 2. Structural Engineering and Disaster Prevention Research Institute, Yangtze University, Jingzhou 434023, China)

Detailed finite element analysis (FEA) model was established to investigate the shear performance of square concrete-filled steel tubular (CFST) column to steel beam joint with external diaphragm under seismic loading on the basis of the size of the joint in test. The material non-linearity, the damage degradation of concrete under cyclic loading and the interaction between steel and concrete were considered in this model. Experimental result was compared to validate the feasibility of this model in simulating the behavior of the composite joints in cyclic loading. Simultaneously, parametric studies were carried out to study the influence of the following parameters on the shearing capacity and deformation in panel zone: ratio of width to thickness of column, the concrete strength of panel zone, the axial load ratio of the column and the ratio of depth to width of panel zone. Eventually, a shear force-deformation restoring-force model of panel zone in composite joints was proposed. The results show that the restoring-force model is practical and can provide practical basis for engineering design.

concrete filled steel tubular (CFST) column-steel beam joint with external diaphragm; finite element analysis (FEA); reinforced concrete (RC) slab; shear performance

TU317.1

A

1672−7207(2018)01−0226−12

10.11817/j.issn.1672-7207.2018.01.029

2017−01−01；

2017−03−20

国家自然科学基金资助项目(51778064, 51378077)；湖北省自然科学基金(创新群体)资助项目(2015CFA029, 2016CFA022)；中国石油科技创新基金资助项目(2016D-5007-0605) (Projects(51778064, 51378077) supported by the National Natural Science Foundation of China; Projects (2015CFA029, 2016CFA022) supported by the Natural Science Foundation of Hubei Province (Innovation Group); Project (2016D-5007-0605) supported by Petroleum Science and Technology Innovation Foundation of China)

杜国锋，博士，教授，硕士生导师，从事智能材料与结构、工程结构抗震研究；E-mail: gfd_1125@126.com