An investigation on adaptively machining the leading and tailing edges of an SPF/DB titanium hollow blade using free-form deformation
2018-02-02ZhengciZHAOJiuhuXUYucnFUZhiqingLI
Zhengci ZHAO,Jiuhu XU,Yucn FU,*,Zhiqing LI
aCollege of Mechanical and Electrical Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
bBeijing Aeronautics Manufacturing Technology Research Institute,Beijing 100024,China
1.Introduction
Titanium hollow blades are very popular in aerospace application with the advantages of lightweight and high damping level,which have been a pivotal option for high thrust-toweight turbine engines.1–4Because of their hollow structures,traditional machining technologies such as forging,casting,and milling,cannot be used to manufacture this kind of blades.Superplastic forming and diffusion bonding(SPF/DB)is a technique allowing for manufacturing hollow metallic sandwich parts with an internal structure,which is based on the superplasticity and bondability of metal materials.5–7Since titanium alloys exhibit great performance of superplasticity and diffusion bondability,titanium hollow blades are formed by the SPF/DB process nowadays.8,9However,a critical problem occurs in this process.Although the SPF/DB process can form the desired internal structure of a blade,it is hard to form the leading and tailing edges simultaneously,which are circle arc lines or quadratic curves with a high requirement of machining accuracy.Thus,a numerical control(NC)milling operation is often employed after the SPF/DB process to manufacture the leading and tailing edges.10,11SPF/DB is a hotforming process in which titanium alloys undergo multiple cycles of high temperature and pressure,leading to a global deformation of the hollow blade.Because the leading and tailing edges have a small allowance to be removed in the NC milling operation,the heat-induced global deformation makes it impossible to manufacture the edges depending on the original nominal CAD model of the blade.Although this global deformation problem is inevitable for SPF/DB,it has a small effect on the aerodynamic performance of the hollow blade.Hence,if the nominal CAD model of the blade can be slightly and correctly modified,like twisting and scaling,to adapt to the actual deformed shape of the hollow blade,it can dramatically reduce the rejection rate and save the production cost.This paper attempts to propose a quick and convenient approach to adaptively manufacture the leading and tailing edges of a hollow blade previously formed by the SPF/DB process.
The critical issue in adaptively machining the leading and tailing edges of a hollow blade is how to reconstruct a new nominal CAD modelfitted to the deformed shape.Many previous works have been carried out in geometric reconstruction of blades.Lin et al.12presents a geometric reconstruction approach for solving the disconnection problem between the actual surface of a blade and the theoretical model in the areas of the leading and tailing edges.They dealt with modifying each cross-section of a turbine blade separately by searching new arc radii and center points as well asfitting lines around the connection area.Wang et al.13put forward a method to remanufacture and repair damaged blades,in which the point cloud of broken blades was obtained and processed and a 3D digital model was built on the boundary section curves extracted from the point cloud.Piya et al.14used sectional Gauss sections to generate a series of prominent cross sections to rebuild a CAD model for remanufacturing gas turbine blades.Mavromihales et al.15obtained the point cloud of a hollow fan blade with afive-axis center,which was imported into reverse engineering software for CAD model reconstruction.Gao et al.16scanned a worn blade and loaded the scanned data into the reverse engineering software of Polyworks for tip reconstruction.
As described above,previous related works have mainly focused on the geometric reconstruction of worn blades for remanufacturing or repairing.Besides,the reconstructed geometry wasfitted from a large number of scanned points.Scanning,processing of points data,and geometricfitting are all time-consuming and labor-intensive.Free-form deformation(FFD)is a modelling technique for quickly reshaping an object by warping the surrounding space17,which is widely used in computer graphics and film animation.FFD wasfirstly proposed by Sederberg and Parry18,which deforms a solid geometric model in a free-form manner based on trivariate Bernstein polynomials.Coquillart19extended FFD in which arbitrarily-shaped bumps can be designed and surfaces can be bent along arbitrarily-shaped curves.Kobayashi and Ootsubo20presented a t-FFD method,by which the original shape of a polygonal mesh or point cloud is deformed using a control mesh.Up to now,volume-based,surface-based,curve-based,and point-based FFD technologies have been developed to satisfy different requirements from a user-centered perspective.17
This paper intends tofind a quick and convenient approach for adaptively machining hollow blades using an improved ICP algorithm and an FFD volume based on on-machine measurement point data,by which thefinal nominal shape can be accurately modified in a controllable amount to make the leading and tailing edges be manufactured successfully.The rest of this paper is organized as follows.The problem description and solving methodology are given in Section 2.Section 3 details the implementation of the proposed adaptive machining method.The results of a case study and some related discussion are presented in Section 4.Finally,conclusions are summarized in Section 5.
2.Problem description and solving methodology
2.1.Problem description
In traditional NC machining,the nominal shape of a part is the shapefinally wanted by designers or manufacturers,which plays an indispensable role in multi-axis NC programming.It is necessary for a blank with a non-negative allowance to be removed from thefinal nominal shape of the part.Fig.1 schematically illustrates the relation between nominal and actual SPF/DB shapes,and thefinal nominal shape for a milling operation.It can be seen that the actual SPF/DB shape has a deviation compared to the nominal SPF/DB shape.Because the nominal SPF/DB shape only has a slight allowance in the areas around the leading and tailing edges,the deviation between the actual and nominal SPF/DB shapes causes that thefinal nominal shape cannot be totally enveloped by the actual SPF/DB shape.In other words,the actual SPF/DB shape has a negative allowance,which is impossible for traditional NC machining to manufacture the leading and tailing edges of the hollow blade.This problem results in a high rejection rate and an expensive production cost,which limit the application of hollow blades in aerospace engineering.Besides,it can be seen from Fig.1 that only the areas around the leading and tailing edges(Zones A and C)are manufactured with the NC milling process,while Zone B will be polished using multi-axis belt grinding after NC milling.A disconnection problem will occur in the adjacent areas between Zones A and B and Zones B and C,which also cannot be solved by the following belt grinding process.This problem will be discussed in our future papers.
2.2.Solving methodology
Since the traditional NC machining process cannot solve this problem,a new machining approach should be developed.Fig.2 presents theflowchart of the adaptive machining approach proposed in thispaper.Firstly,on-machine measurement is used to inspect the shape of the actual SPF/DB blade to acquire the point cloud data.The point data is then matched to the nominal SPF/DB shape to evaluate whether thefinal nominal shape can be totally enveloped by the measured points.If yes,the actual SPF/DB blade can be machined to thefinal nominal shape by the traditional NC machining process.If not,the FFD volume of the SPF/DB shape is calculated based on the vector displacements between the point-pairs built in the registration process.An iterative process is introduced in the FFD calculation to improve the calculation accuracy.A threshold value ε is given to judge whether the deformation error is acceptable.If not,a refinement operation of the FFD calculation lattice is employed.Afterwards,the calculated FFD volume of the SPF/DB shape is applied to thefinal nominal shape,in which thefinal nominal shape of the blade is modified.Finally,the modified final nominalshapeisused to generatethetoolpath by computer-aided manufacturing(CAM)technology for adaptive machining of the leading and tailing edges.In our proposed approach,the key issues are how to deform thefinal nominal shape and how to control the amount in the FFD volume calculation process.The details of the proposed approach are presented in the following section.

Fig.1 Schematic of the relation between the nominal and actual SPF/DB shapes,and thefinal nominal shape.

Fig.2 Flowchart of adaptive machining.
3.Implementation of adaptive machining
3.1.On-machine measurement
To achieve a newfinal nominal shape of the hollow blade,the only reference is the actual SPF/DB shape,which is individual and unknown.A measurement method is needed to inspect the shape and acquire the point data of the shape.The coordinate measuring machine(CMM)is characterized with high accuracy and versatility,which has a widespread application in aerospace and manufacturing engineering.However,a part should be moved from a machine tool to a measuring device during the machining process,which can induce additional clampingerrorsandincreasethemachiningtime.Onmachine measurement(OMM)is one extension of the CMM,which uses a machine tool as a carrier for a probe.Thus,measurement and machining are performed on the same machine tool with the samefixture,which results in a dramatical reduction in machining cost and avoids unnecessary errors.
Measurement points generation,path planning,and data processingarethreetypicalphasesin theCMM and OMM.21–23The distribution of the generated measurement points has a significant effect on the calculation accuracy of the following algorithms and their computational costs.Due to the space limitation of this paper,how to generate measurement points for adaptively machining hollow blades will be studied in our future paper.In this paper,a special and relevant issue related to the accuracy of measuring an SPF/DB hollow blade is discussed.As known in OMM,the position of a measurement point equals to the sum of the probe center position and the radius compensation along the normal direction of the measurement point,which is formulated as where Pmis a vector from the coordinate origin to the measurement point Pm,The following symbols are expressed similarly as this.Pcis the probe center,Ris the probe radius,and nmis the unit normal vector on the measurement point of the surface,which is calculated from the CAD model.For an SPF/DB hollow blade,the actual SPF/DB shape(SR)has undergone some deformations from the nominal SPF/DB shape(Sn).Pnis the planned measurement point fromSnand n is its unit normal vector.In a practical measurement process,Pdis the actual point to be measured onSRcorresponding toPnonSn.Ideally,Pdcan be calculated as


where n′is the actual unit normal vector ofPd.However,n′is unknown and replaced with n.Thus,the probe is triggered atPr,which can be recorded in the machine tool as

wherePris the actually probed point,P′ris the recorded point,andPcris the probe center ofPr.It can be seen from Fig.3 that there is a deviation betweenPrandP′rbecause of the wrong unit normal vector.The recordedP′ris not onSR,which means that the shape formed by actual measurement points is not the correct shape of the scannedSR.

Snis represented in a format of non-uniform rational B-splines(NURBS),which is formulated as


Fig.3 Schematic diagram of the probe contacting with the deformed shape.
wherePi,jis the control point andwi,jis the weight ofPi,j.mandnare the numbers of lattice grids.uandvare the local parameters.Ni,p(u)andNj,q(v)are the NURBS basis functions of the degreespandqwhich are defined on the knot vectors of

The tangential directions inuandvshould be computed tofind the normal direction of an arbitrary point onSnas follows:

whereTu(u,v)andTv(u,v)are the tangential directions in theuandvdirections,respectively.The cross-product ofTu(u,v)andTv(u,v)is the normal direction onSn,which is written as

The offset surface ofSnis specified as

3.2.Registration using improved ICP algorithm
As shown in Fig.3,the actual measured pointPronSRhas a large deviation to the planned measurement pointPnonSn.Thus,Pris not the corresponding point ofPn.Finding the corresponding point onSnfor each measured point is essential for the allowance evaluation and the FFD volume calculation.Iterative closest point(ICP)registration canfind the closest points on a geometric entity to given points,which is formulated as

whereXiis the corresponding point on the surfaceOn(u,v),Piis the measured point,andNpis the number of measurement points.qTand qRare the translational and rotational matrices,respectively.This least square problem can be solved by singular value deposition.When the solutions of qTand qRare obtained,the coordinates of the measured points can be updated,and the corresponding points are found on the surface.
As shown in Fig.4,d+andd-are the positive and negative tolerances of the nominal shape.After ICP registration,the distancesdifrom the measured points to thefinal nominal shape are calculated.Ifdi>d-for all the measured points,this part can be manufactured by a traditional machining process.If not,adaptive machining is needed.In adaptive machining,the measured points are the targets of FFD volume calculation.The registration result nominally determines the deviation between the modified and original shapes.Hence,a threshold value ξ is introduced to restraint the largest modifi-cation amount of the original shape in the registration process.
niis defined as the unit normal direction ofXi,and thus the modified pointx′ican be approximately written as


Fig.4 Schematic diagram of the measured points,nominal SPF/DB shape,andfinal nominal shape.
whereaiis the nominal allowance ofXi.The distancedibetweenx′iand the final nominal shape is calculated as

where xi=Xi-ni·ai,which is the point on the final nominal shape.
Hence,Eq.(9)can be rewritten as

By solving Eq.(12),a new coordinate of the measured points is updated and the new corresponding point for each measured point is found,by which thefinal nominal shape can be modified in a controllable amount.
3.3.FFD volume calculation
Free-form deformation warps the embedding space around an object and thus implicitly deforms the object,which represents the space deformation by a trivariate tensor-product spline function as

where δijkare the displacements of the lattice control pointcijkbefore and after the space deformation.l,m,andnare the numbers of lattice grids,andu,v,andware the local parameters of a point inside the B-spline volume.Ni,p(u),Nj,q(v),andNk,r(w)are the basis functions of B-spline of the degreesp,q,andr,which are defined on the knot vectors of


In our application of adaptive machining,the displacements from the measured points to their corresponding points have been obtained,which means thatd(u,v,w)is known.If δijkcan be inversely calculated according to Eq.(13),the whole deformation volume of the embedding space is achieved.
This inverse calculation can be formulated as a least-square problem,that is,

which can be solved by a singular value deposition method.
The lattice size has a great effect on the calculation accuracy and efficiency of the FFD algorithm.As described above,building a local coordinate system based on each lattice point is necessary at the beginning of the FFD calculation.Point inversion is often used to build this local coordinate system,which is time-consuming.As described in Eq.(13),a trivariate tensor-product spline function is used to represent the space deformation.If an original lattice is set as 4×4×4,the space deformation is equal to a Bezier space,and point inversion is not needed any more.Hence,we set a lattice of 4×4×4 in this paper first,and then an iterative approach of refining the FFD volume from the original lattice by knot insertion is used to improve the calculation accuracy of the FFD volume,which can save the computational cost dramatically.The challenge is tofind where is the largest deviation in the iterative process.Sacharow et al.24firstly divided the FFD volume into cells,and then compared the deformed shape with the targets to locate the cells with a large error,which was formulated as

whereLis the length of the cell,Mis the maximum length of all deformation vectors,and bx= [1,0,1]T.ndis the number of vectors andkis fork-neighborhood.The cells withC≥ε would be refined by inserting new knots.
For adaptively machining a hollow blade,the FFD volume is calculated based on the measured points from the actual SPF/DB shape and their corresponding points on the nominal SPF/DB shape.Thefinal nominal shape is embedded in the deformation space.When the iterative calculation isfinished,a newfinal shape is achieved with the deformed embedding space.Because a threshold value ξ has been introduced in the registration process,the calculated FFD volume can modify thefinal shape of the hollow blade with a controllable amount.
4.Results and discussion
To validate the feasibility of the adaptive machining approach proposed above,a machining test of one certain hollow blade is presented in this section.A validating test was performed in accordance with the procedure in Fig.3.Measurement and milling tests were carried out on a DMG Linear 5-axis machine center,which has a maximum spindle speed of 42000 r/min and a traverse rangeX/Y/Zof 200/200/280 mm.The algorithms were run on a 64-bit Windows workstation with a 2.9-GHz processor and 32-GB memory.Fig.5 presents the nominal SPF/DB shape and thefinal nominal shape of the hollow blade,which was made of a typical titanium alloy Ti-6Al-4V.The nominal shape has a length of 280 mm and a width of 140 mm.It is shown from Fig.5 that the hollow blade has an internal structure of honey-comb sandwich formed by the SPF/DB process.The SPF/DB shape is the near-net shape of the blade,on which the leading and tailing edges have a small amount of allowance to be removed.Besides,for this testing part,thefinal nominal shape is tangential to the nominal SPF/DB shape at points A and B.Hence,the disconnection problem does not exist in the following machining tests.
The experimental setup of OMM is presented in Fig.6,in which the hollow blade was secured to afixture with two bolts and placed on the worktable of the machine tool.A Renishaw trigger probe was loaded on the main spindle for the measuring operation.Once the stylus touched the blade,the probe sent a triggering signal to the machine tool,and the NC system recorded the current position of the spindle.Fig.7 shows the distribution of the planned measurement points of the hollow blade.23 sections with 25 points in each section were generated on the nominal SPF/DB shape.As discussed above,the probe center positions were recorded for the accuracy requirement.Hence,the planned measurement points were generated on the offset shape of the nominal shape with a value of the probe radius.As shown in Fig.7,one top point was used to control the deformation of the blade along the chordwise direction,and side points were used to control the twisted deformation of the blade.
After the measurement data were obtained,the ICP algorithm was employed to match the measured points to thefinal nominal shape.Fig.8 shows the comparison results of the measured points and thefinal nominal shape.The maximum negative deviation is-1.905 mm,which means that there is no allowance to be removed,and thefinal nominal shape cannot be achieved by the traditional NC machining method.Thus,adaptive machining should be employed.The measured points werefirstly matched to the nominal SPF/DB shape using the improved ICP algorithm to update a new coordinate and build new point-pairs.By considering the actual dimensional state of the testing blade,we set ξ as 1 mm.The calculation time of this case was around 5.207 s.Fig.9 shows the registration result,in which the maximum absolute value of the deviation is 0.969 mm.Based on these point-pairs,an FFD volume was iteratively calculated with ε=0.01 mm.The time of calculating this case was about 9.533 s.Three iterative steps were performed,and the maximum calculation error is 0.0056 mm with a lattice of 7×7×8.

Fig.5 Nominal SPF/DB shape andfinal nominal shape of a fan blade.

Fig.6 Experimental setup of OMM.
Thefinal nominal shape was embedded in the deformation space,and a modified final shape was achieved with the deformed lattice control points.Fig.10 presents the comparison results of the modified final shape and some sampled points from its original shape.It can be seen that the original shape was totally modified by changing the embedding space.Themodification amountrangesfrom -0.527 mm to 1.082 mm.This modification was caused by the deviation between the actual and nominal SPF/DB shapes.The FFD algorithm was employed to modify thefinal nominal shape to be enveloped totally by the actual SPF/DB shape.The modified final shape was offset by a value of the probe radius in Fig.11,which was compared with the measured points from the actual SPF/DB shape.The results show that all the machining allowances on the modified final shape are nonnegative,and the maximum allowance is 1.413 mm.The comparison result of the allowance distribution before and after the FFD calculation is summarized in Table 1.It can be seen thattheminimum allowancehasbeenmodifiedfrom-0.969 mm to 0 mm,which ensures that the testing blade can be milled successfully.The allowance distribution of the modified final shape was decided by the distribution of the nominal shape and the deformation of the embedding space.Approximately,thefinal allowance distribution equals to the scale caused by the FFD volume of the original allowance distribution.The scaling factor is determined by the deviation between the actual and nominal SPF/DB shapes.Hence,the actual SPF/DB decides the modified final shape and its allowance distribution,which is so-called adaptive machining.
Based on the modified final shape,a machining test was conducted on a DMG Linear 5-axis machine center.The experimental setup was similar to the measurement test,in which a trigger was replaced by a ball endmill with a diameter of 10 mm.Fig.12 presents the manufactured hollow blade by the proposed adaptive method,one edge of which was machined successfully in one NC milling path.The results of the machining test have shown that the proposed adaptive machining by using FFD is feasible.
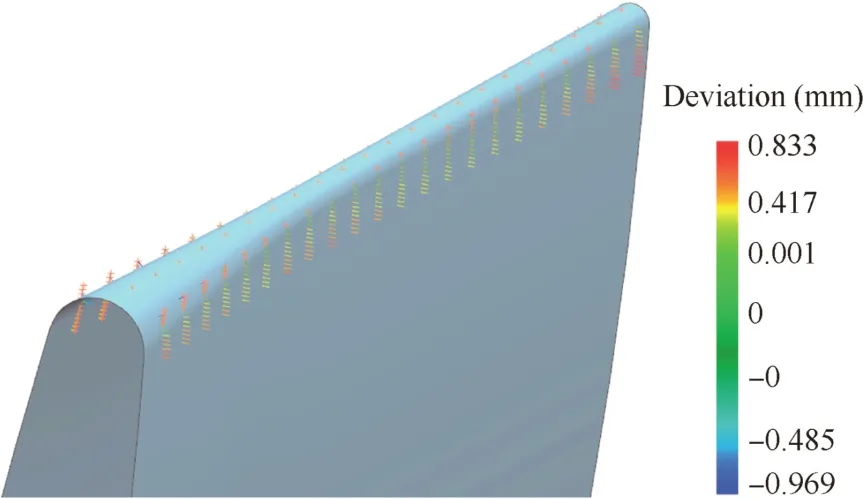
Fig.9 Registration results of the measured points and thefinal nominal shape.

Fig.10 Comparison results of the modified final shape and sampled points from the original shape.

Fig.11 Comparison results of the measured points and the offset modified final nominal shape.

Table1 Allowancedistribution beforeand afterFFD calculation.

Fig.12 Hollow blade after adaptive machining.
5.Conclusions
An integrated adaptive approach for manufacturing the leading and tailing edges of an SPF/DB hollow blade has been presented in this paper,which includes on-machine measurement,registration,and iterative FFD calculation.The error of measuring the deformed shape according to the nominal shape was analyzed.An improved ICP algorithm was developed to control the modification amount of the final nominal shape in the registration process.An iterative FFD volume was employed to deform the embedding space according to the displacements between measured points from the actual SPF/DB shape and their corresponding points on the nominal SPF/DB shape.Thefinal nominal shape was embedded in the deformation space,and a newfinal shape of the hollow blade was obtained.The results of the measurement and machining tests revealed that this adaptive machining approach is feasible in machining the leading and tailing edges of an SPF/DB hollow blade.
Acknowledgements
The authors gratefully acknowledge thefinancial supports of the NationalNaturalScience Foundation of China(No.51475233),the Fundamental Research Funds for Central Universities(No.NZ2016107),and the Jiangsu Innovation Program for Graduate Education(No.CXLX13_139).
1.Li X,Sun B,You HD,Wang L.Evolution of Rolls-Royce aircooled turbine blades and feature analysis.ProcEng2015;99:1482–91.
2.Cowles BA.High cycle fatigue in aircraft gas turbines-an industry perspective.Int J Fract1996;80(2):147–63.
3.Grujicic M,Arakere G,Pandurangan B,Yen CF,Cheeseman BA.Process modeling of Ti-6Al-4Al linear friction welding(LFW).J Mater Eng Perform2012;21(10):2011–23.
4.Zhao B,Li ZQ,Hou HL,Liao JH,Bai BZ.Three dimensional FEM simulation of titanium hollow blade forming process.Rare Metal Mater Eng2010;39(6):0963–968.
5.Sanders DG,Ramulu M,Edwards PD,Cantrell.Effects on the surface texture,superplastic forming,and fatigue performance of titanium 6AL-4V friction stir welds.J Mater Eng Perform2010;19(4):503–9.
6.Ramulu M,Edwards PD,Sanders DG,Reynolds AP,Trapp T.Tensile properties of friction stir welded and friction stir welded superplastically formed Ti–6Al–4V butt joints.Mater Des2010;31(6):3056–61.
7.Palumbo G,Brandizzi M.Experimental investigations on the single point incremental forming of a titanium alloy component combining static heating with high tool rotation speed.Mater Des2012;40:43–51.
8.Zhang TY,Liu Y,Sanders DG,Liu B,Zhang WD,Zhou CX.Development offine-grain size titanium 6Al-4V alloy sheet material for low temperature superplastic forming.Mater Sci Eng A2014;608:265–72.
9.Balasubramanian M,Ramanathan K,Kumar VSS.Mathematical modeling andfinite element analysis of superplastic forming of Ti-6Al-4V alloy in a stepped rectangular die.ProcEng2013;64:1209–18.
10.Zhou X,Zhang DH,Luo M,Wu BH.Chatter stability prediction in four-axis milling of aero-engine casings with bull-nose end mill.Chin J Aeronaut2015;28(6):1766–73.
11.Xu RF,Chen ZT,Chen WY,Wu XZ,Zhu JJ.Dual drive curve tool path planning method for 5-axis NC machining of sculptured surfaces.Chin J Aeronaut2010;23(4):486–94.
12.Lin XJ,Chen Y,Wang ZW,Guo Y,Gao Y,Zhang YG.The research of model restructuring about leading edge and tailing edge of precision forging blade for the adaptive machining technology.Acta Aeronaut Astronaut Sin2015;36(5):1695–703[Chinese].
13.Wang H,Wang LW,Wang T,Ding HP.Method and implementation of remanufacture and repair of aircraft engine damaged blades.Acta Aeronaut Astronaut Sin2016;37(3):1036–48[Chinese].
14.Piya C,Wilson JM,Murugappan S,Shin Y,Ramani K.Virtual repair:geometric reconstruction for remanufacturing gas turbine blades.IDETC/CIE 2011:international design engineering technical conferences and computers and information in engineeringconference,2011 August 28–31.Washington,DC,USA.New York:American Society of Mechanical Engineering;2011.p.1–10.
15.Mavromihales M,Mason J,Weston W.A case of reverse engineering for the manufacture of wide chord fan blades(WCFB)used in Rolls Royce aero engines.J Mater Process Technol2003;134(3):279–86.
16.Gao J,Chen X,Yilmaz O,Gindy N.An integrated adaptive repair solution for complex aerospace components through geometry reconstruction.Int J Adv Manuf Technol2008;36(11):1170–9.
17.Gain J.A survey of spatial deformation from a user-centered perspective.ACM Trans Graph2008;27(4):107,1–20.
18.Sederberg TW,Parry SR.Free-form deformation of solid geometric models.ACM SIGGRAPH1986;20(4):151–60.
19.Coquillart S.Extended free-form deformation:a sculpturing tool for 3D geometric modeling.Comput Graph1990;24(4):187–96.
20.Kobayashi K,Ootsubo K.t-FFD:free-form deformation by using triangular mesh.Proceedings of the eighth ACM symposium onsolid modeling and applications;2003 June 16–20;Seattle,USA.New York:ACM Press;2003.p.226–34.
21.Mansour G.A developed algorithm for simulation of blades to reduce the measurement points and time on coordinate measuring machine(CMM).Measurement2014;54:51–7.
22.Obeidat S,Raman S.An intelligent sampling method for inspecting free-form surfaces.Int J Adv Manuf Technol2009;40(11–12):1125–36.
23.Poniatowska M.Deviation model based method of planning accuracy inspection of free-form surfaces using CMMs.Measurement2012;45(5):927–37.
24.Sacharow A,Surmann T,Biermann D.Adaptive free-form deformation for the modification of CAD/CAM data.ADVCOMP 2011:thefifth international conference on advanced engineering computing and applications in sciences,2011 November 20–25.Lisbon Portugal.Wilmington:IARIA;2011.p.27–31.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Guide for Authors
- An aviation oxygen supply system based on a mechanical ventilation model
- Influence of TiB2particles on machinability and machining parameter optimization of TiB2/Al MMCs
- Analysis of the cylinder block tilting inertia moment and its effect on the performance of high-speed electro-hydrostatic actuator pumps of aircraft
- A direct position determination method with combined TDOA and FDOA based on particlefilter
- Rapid and robust initialization for monocular visual inertial navigation within multi-state Kalmanfilter
