Rapid and robust initialization for monocular visual inertial navigation within multi-state Kalmanfilter
2018-02-02WeiFANGLianyuZHENG
Wei FANG,Lianyu ZHENG
School of Mechanical Engineering and Automation,Beihang University,Beijing 100083,China
Navigation for an isolated target,providing the position,orientation,and velocity of the object in an unprepared environment,is a great challenge in the community of Unmanned Aerial Vehicles(UAVs),1–3mobile robot,4augmented reality,5etc.With an accurate state estimation,the target object can percept the current pose and do the decision-making for the next step,and this technology is becoming ubiquitous in our daily life.
Much work has been done to achieve this assignment,and the visual-based approach is typical one for the pose estimation and the surrounding perception.Liu et al.6presented a high-precision pose estimation based on a binocular vision,and the pose can be estimated in real time with the highspeed cameras and laser scanning.As an outside-in capturing style,this method needs to arrange the location and orientation of the observed equipment in advance to avoid the occlusion,lacking generality andflexibility for free moving targets’navigation.Zhou and Tao7proposed a vision-based navigation method by using marked feature points arranged in a radial shape.Instead of the traditional locating method by PnP,the camera location and outlier points are calculated simultaneously,making the navigation more efficient.Nevertheless,this maker-based navigation method can achieve considerable accuracy only at the expense of the prior knowledge about the scene.
With the progress of the lightweight and cheap microelectro-mechanical system,the Inertial Measurement Unit(IMU)can provide the position,orientation and velocity passively.However,these consumer-grade IMUs are influenced greatly by the time integration of the systematic error and must be corrected periodically.As a common complementary sensor,the Global Positioning System(GPS)is usually used for this correction,8but it cannot work in the GPS-denied environment for an indoor navigation.9Thus,Zhu et al.10proposed an indoor positioning method by fusing the WiFi and inertial sensors,but WiFi signals are not available everywhere,limiting a wider application of this method to some extent.As described in the last paragraph,6,7although there are some limitations by the vision-only navigation method,the accuracy of these pose estimations is reliable.Moreover,the consumer-grade camera and IMU module are ubiquitous in our daily life.For smallsize and light-weight applications,such as UAVs and mobile devices,the monocular camera turns out to be a superior visual candidate sensor.Thus,the integrated navigation by combining a monocular camera and an inertial sensor is applied in the paper.
In addition,the visual inertial navigation can be categorized into filtering-based11oroptimization-based.12Thefiltering-based approach requires fewer computational resources by marginalizing past states,but this method may have slightly lower performance due to the earlyfixing of linearization points.However,the optimization-based approach results in a better performance at the expense of higher computational demands.The comparison betweenfiltering-based and optimization-based approaches is detailed.13Taking the realtime application in the future UAV-like resource-constraint system for consideration,this paper focuses on thefilteringbased fusion method with a high efficiency.According to the different combinations of visual and inertial information,thefiltering-based sensor fusion solution can be further grouped into loosely-coupled14,15and tightly-coupled.16,17The loosely-coupled approach usually consists of a standalone vision-based pose estimation module,such as SVO18or ORB-SLAM,19and a separate IMU propagation module.15Due to the lack of cross-relation information between the vision and IMU,the loosely-coupled system is incapable of correcting drifts in the estimator.Tightly-coupled approach performs systematic fusion of the visual and IMU measurements,usually leading to better navigation results.12What is more,as a monocular navigation,the arbitrary scale is a common problem,and the tightly-coupled method is able to implicitly incorporate the metric information from IMU into the 3D scene estimation,removing the need for scale modeling individually.Thus,the tightly-coupled method is adapted for our monocular visual inertial navigation.
The most common tightly-coupled visual inertial navigation is to augment the 3D feature positions in thefilter state,and concurrently estimates the pose and 3D points.17This method leads to an increasing computational complexity with new observed features.To address this problem,the Multi-State Constraint Kalman Filter(MSCKF),16instead of estimating the positions of landmarks in the state vector,maintains constant computational demands by a sliding window of camera poses.Compared with the traditional visual inertial navigation in Extended Kalman Filter(EKF),the MSCKF method can balance the efficiency and accuracy within a larger-scale navigation.After the presentation of the MSCKF,a number of improvements have been applied,20,21and they increased the accuracy and online calibration performance for MSCKF.Gui and Gu22proposed a keyframe within the direct approach in MSCKF,and it can reduce the computational complexity linear to the number of selected patches.However,due to minimum length constraint of sliding windows for state update,the initialization problem in MSCKF is still unsolved.Usually,the sensor module had better be kept static for a while to achieve initialization,and shocks at the initial stage may damage the initialization performance in MSCKF.As a highly nonlinear system by fusion of visual and IMU measurements,an accurate and robust initialization is required to bootstrap the estimator.Hesch et al.11had shown that the performance of visual inertial navigation estimator relied heavily on the accuracy of initial state,and the initialization error would be accumulated in the subsequent navigation.In recent years,researchers have made some achievements on the initialization of the visual inertial navigation.Yang and Shen23addressed the initialization problem based on optimization-based method.They divided the estimation pipeline into different stages,and the experimental results illustrated the validity of the method.But the optimizationbased initialization is of high computational complexity,and the state vector derived from the optimization-based initialization is not consistent with the subsequent MSCKF.
To the best of our knowledge,this is thefirst paper which pays attention to the initialization within MSCKF framework for visual inertial navigation.In order to improve the initialization performance of MSCKF,a trifocal tensor constraint based Initialization MSCKF(I-MSCKF)method is proposed.Instead of calculating the 3D map points in the scene,the constraints between successive three images are applied to the initial estimator.At the same time,the estimated poses are generated and accumulated to satisfy the minimum sliding window for MSCKF.In addition,in order to improve the initialization accuracy,the sigma-pointfilter is applied to providing superior approximation for the nonlinear system.Thus,with the proposed I-MSCKF method,the robustness and accuracy of initialization can be improved,resulting in a superior performance for the monocular visual inertial navigation.The overall workflow of the proposed I-MSCKF method is depicted in Fig.1.The combination of trifocal tensor and sigma-pointfilter is applied to the initialization,and then the seamless transform for the subsequent state estimation is provided to MSCKF.Finally,the state estimation can be output by the monocular visual inertial navigation.
The following sections are organized as follows.Section 2 introduces the IMU propagation model and the MSCKF method.In Section 3,the trifocal tensor and the sigma-pointfilter for initialization are depicted.In Section 4,the performance of the proposed I-MSCKF method is demonstrated by different experiments.Finally,the conclusions of the study are summarized in Section 5.

Fig.1 Overallflowchart of visual inertial navigation.
2.State estimate and MSCKF
2.1.IMU propagation model
The state propagation is carried out from IMU measurements,and a 16-dimensional vector is parameterized for IMU state in the paper:

whereIGq is the quaternion representing the rotation from the global frame {G} to the IMU frame {I},GvIandGpIare the velocity and position of the IMU in the global frame,respectively,and bωand badenote the biases of the gyroscope and accelerometer,respectively.
Using the continuous-time dynamics of the state,Eq.(2)can be obtained.

whereGa is the acceleration in the global frame,nbωand nbaare the Gaussian random walk process of the biases bωand ba,respectively,and Ω(ω)is the quaternion multiplication matrix of ω,which can be defined by

Given the gyroscope(accelerometer)in a inertial sensor,their outputs contain a certain bias bω(ba)and white Gaussian noise nω(na).With the measurements ωmand amfrom the gyroscope and accelerometer,the real angular velocity ω and the real acceleration a can be obtained:

With the linearization of Eq.(2),the continuous-time nominal state propagation model can be achieved:


whereGδθIis the angle deviation of the error quaternion δq,and then the 15-dimensional IMU error state is obtained:

2.2.State propagation
Different to the visual aided inertial EKF-fusion method,17the MSCKF method does not add features to the state vector.And the update procedure is carried out when features are out of view or the number of appending poses reaches to the maximum length threshold.In other words,the state vector of MSCKF maintains a sliding window of camera poses.As shown in Fig.2,ncamera poses andmfeatures are visible to each other,and thus featuresfi(i=1,2,...,m)can be used to impose constraints to all camera poses in the sliding window.In our monocular visual inertial navigation,the main purpose of MSCKF is to estimate the orientation and position of the IMU-affixed frame {I} in a global frame {G},and states of the camera can be obtained by the rigid connection with the IMU.At time stepk,the full state vector consists of the current IMU state estimate andn7-dimensional past camera poses.Thus the vector has the following form:


Therefore,theerrorstatevectorofMSCKFcanbedefinedas


Fig.2 Schematic of MSCKF constraint framework.

Infilter prediction,IMU measurements for state propagation are obtained in a discrete form,and thus the signals from gyroscope and accelerometer are assumed to sample at a certain time interval.By combining Eqs.(2)and(4),the IMU error-state kinematics can be obtained:

Thus,the linearized continuous-time model of the IMU error state24is acquired:


where I3is the 3×3 identity matrix,and G is calculated as follows:

2.3.State augmentation



where I6n+15is a (6n+15)× (6n+15)identity matrix,and the Jacobian Jkis derived from Eq.(13).

2.4.Covariance propagation

Given the computational complexity,the Euler method for integration over sampling time Δtis chosen.Thus,the discretetime error state transform matrix Φ(tk+ Δt,tk)can be derived as Eq.(17)according to method12:


where QIis the covariance matrix of the IMU process noise nIin Eq.(10).
2.5.State correction



Now that we have estimated the position of any feature in the state,the measurement residual is obtained:

Linearize Eq.(21)about the estimates for the camera poses and feature positions,and the residual can be estimated approximately:





In order to reduce the computational complexity of this EKF update,a QR decomposition for Hois employed.

where Q1and Q2are the unitary matrices and THis an uppertriangular matrix.Substituting the result into Eq.(25)and multiplying by [Q1,Q2]Tyield:

The residual QT2rocan be discarded as noise,and a new error term can be defined for the EKF update:



At the same time,the correction and the updated estimate for covariance matrix are formulated as


3.Rapid and robust initialization method
As depicted in Section 2,due to a certain sliding window constraint,the visual inertial fusion based on MSCKF can maintain a tradeoff between accuracy and efficiency.However,at the initial stage of MSCKF,a certain length of sliding window is needed to bootstrap the subsequent state estimator.Usually,the navigation objects should be kept static for a while for a successful initialization.Otherwise,the initial error would deteriorate the sequential navigation performance.To alleviate the limitation,a trifocal tensor and sigma-pointfilter based initialization method I-MSCKF will be applied as follows.
3.1.Trifocal tensor based constraints

With the constraint about epipolar geometry,the trifocal tensor encapsulates geometric relationships between three different viewpoints.As shown in Fig.4,the geometric properties of the trifocal tensor are introduced.It can transfer points from a correspondence in two views to the corresponding point in a third view.Compared with the epipolar constraint in two viewpoints,the essence of the trifocal tensor is the geometric constraint of a point-line-point correspondence in a 3D-space,enabling a stronger constraint to the pose estimation.
Thus,to improve the initial robustness of MSCKF,a trifocal tensor based state vector can be defined as Eq.(32),and it makes the visual inertial navigation without estimating the 3D position of feature point:


Compared with the MSCKF,the proposed I-MSCKF method can accomplish initialization within three images.At the same time,given the same state vector framework,pose estimations at the initial stage can be accumulated to satisfy the sliding window restriction of MSCKF.Thus,the robustness of initialization is improved when suffered from shocks at initial stage.In addition,to achieve higher initial accuracy,a more accurate sigma-pointfilter is applied in the initial state rather than EKF,and the detailed measurement update process at the initial stage will be illustrated next.

Fig.3 Epipolar geometry between two views.
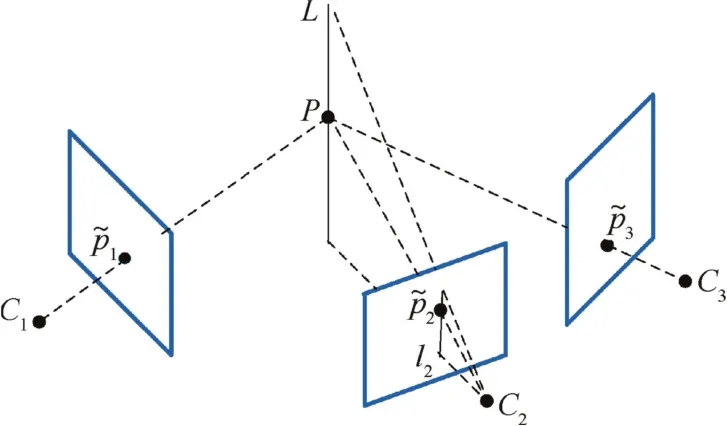
Fig.4 Correspondences between trifocal tensors.
3.2.Initial measurement update
Let the projection matrices of camera for the three views be P1= [I| 0 ],P2= [A′|a4]and P3= [B′|b4],where A′and B′are 3×3 matrices,and the vector a4and b4are the 4th column of the respective projection matrix of camera.Therefore,according to the projection matrix and the line in 3D space,the notation of trifocal tensor can be derived:

where the vectors ai,bi(i=1,2,3)are theith column of the respective projection matrix of camera.


According to the principle of trifocal tensor,the point~m3in the third image is obtained:
Thus,the measurement model can be given by the combination of epipolar and trifocal tensor constraints.Since the trifocal tensor focuses on three consecutive images,assuming that theith correspondence feature point in three images is{m1,m2,m3},two measurement models among three images are acquired:

where (h1,h2)are measurement elements from epipolar geometry,and then with the predicted pose (GRC,GpC)from IMU propagation,the corresponding pairs of (R12,t12),(R23,t23)can be yielded:

According to Eq.(36)and the trifocal tensor constraints,another measurement element is acquired as

Therefore,the total measurement zincan be derived by stacking Eqs.(37)and(39):

where~xinis the initial state from Eq.(33),and with these trifocal constraints at the initial stage of MSCKF,features from thefirst captured image are extracted and stored.Given the state vector in Eq.(33),the IMU propagation model for trifocal tensor is similar to Section 2.2.And then,when each subsequent image arrives,features are extracted and matched to former stored points,and the errors between predicted and measured locations are used to update the state estimation.In MSCKF,there exist a minimum number of observations for a feature track to trigger an update,such as ten or more continuous observed images to accomplish a reliable tracking precision.Thus,the navigation system is supposed to keep stabilization at this initialization stage,otherwise the error within the initialization would destroy the subsequent navigation.With the help of the trifocal tensor constraint,the predicted pose can be corrected within only three continuous images instead of ten or more images in MSCKF.Given that the elapsed time is proportional to the number of images,the initialization time of I-MSCKF can be reduced dramatically.And then,the estimated camera poses by trifocal tensor are appended to satisfy the minimum number of observations in MSCKF framework.Therefore,a rapid and robust initialization for visual inertial navigation can be obtained by the proposed I-MSCKF.
3.3.Sigma-pointfilter
Due to the nonlinearity of the visual inertial navigation,imprecise initialization may irreparably deteriorate the subsequent state estimation.Therefore,a more accurate sigma-pointfilter is used in the paper to apply measurement update at the initial stage.Using the following scheme,the sigma-point can be generated by the state covariance matrix Pkk-1|:


Fig.5 Typical images and estimated trajectories.
wheren=27 is the dimension of initial state vector,and thus the initial state X0can be denoted as 027×1.The weightWsiandWci(i=0,1,...,2n)in the sigma-pointfilter can be acquired as

with λ= α2(n+ κ)-n,α determines the distribution of λ,which is usually set as a small positive,27and it is set to 0.2 in the paper.κ is set as 3-nat parameter estimation.For the Gaussian distribution,β =2 can be defined.With the measurement noise covariance matrix Rin,the measurement model can be obtained as

where Pxziand Pziziare the state-measurementcrosscovariance matrix and the predicted measurement covariance matrix,respectively,and Kinis thefilter gain from the sigmapointfilter.And then,the update of error state and covariance matrix can be carried out within the initial stage.


Table 1 RMSEs of different methods in KITTI dataset.
At the same time,the output pose estimation is accumulated,and the initialization is accomplished when the number of accumulated poses reaches to the sliding threshold of MSCKF.Moreover,with the accurate sigma-pointfilter for pose estimation at initial stage,the proposed I-MSCKF method can achieve better navigation performance.
4.Experiments
In this section,two kinds of the experiments are carried out to evaluate the proposed I-MSCKF method.Thefirst kind of experiments is derived from the public datasets KITTI28and EuRoc29,which are generated by the automobile and UAV with ground truths.They can be applied to quantitative analysis of the proposed method.Another kind of experiments is carried out by our own monocular camera and IMU platform.Due to the lack of ground truth,only qualitative analyses of the I-MSCKF method can be realized.Moreover,to assess the performance of the difference methods clearly,the initial parts of all navigation experiments are chosen with major vibration intentionally.Experimental results and analyses are presented in following sections.

Fig.6 3σ boundaries for pose estimation error with proposed I-MSCKF method.
4.1.Case 1:Navigation for KITTI dataset
The KITTI dataset is a famous algorithm evaluation platform from Karlsruhe Institute of Technology and Toyota Technological Institute at Chicago.It is generated from two grayscale and two color cameras,a laser scanner,and a high-precision GPS/IMU system OXTS RT3003,and the measurement frequency of 6-axis IMU is 100 Hz.What is more,the ground truth along with the motion trajectory is also provided.For our monocular visual inertial navigation,only one grayscale camera and the IMU data are used.
The start point of the navigation near the turning part is chosen intentionally,and typical images of the trajectory are shown in Figs.5(a)and(b).With the dataset from a grayscale camera and an IMU,corresponding trajectories can be estimated from the MSCKF and I-MSCKF(see Fig.5(c)).The ground truth of the trajectory is marked with black solid line,and the results of the MSCKF and the I-MSCKF are illustrated with red dashed line and blue dot dash line,respectively.It is easy tofind that the proposed I-MSCKF method is of high accuracy in the navigation.The reason for this is that the initialization of MSCKF suffered from drastic orientation changes near turning part,making the initial pose estimation from the IMU integration inaccurate.Thus,the optimization of the sliding window cannot converge to an ideal result,leading to the estimated trajectory incrementally deviated to the ground truth.
In order to further analyze the performance of the proposed I-MSCKF method,two different methods are compared with the ground truth.At the time stepk,the Root Mean Square Error(RMSE)can be defined as

whereNis the number of images,pestis the estimated position(orientation)from the state estimation,and pgtis the ground truth of the position(orientation)from the KITTI dataset.RMSEs of these trajectories are shown in Table 1.
Given the robust analysis for the proposed I-MSCKF method,the 3σ boundary of the pose estimations are shown as the dashed line in Fig.6,and the results obtained by the proposed method are depicted as the line within the 3σ boundary.Even with some turning parts during the trajectory,the translational and rotational errors still are located in the 3σ boundaries,illustrating therobustnessoftheproposed method.
4.2.Case 2:Navigation for EuRoc UAV dataset
In addition to evaluating the proposed I-MSCKF method,further experiments on the public EuRoc dataset are performed.This dataset is provided by the ETH Zurich for the UAV navigation algorithm assessment.The experimental platform contains a stereo camera,capturing the images with 20 Hz on a UAV,as shown in Fig.7(a).The synchronized IMU is modeled ADIS16448,which can output the measurements at 200 Hz.The ‘V2_01_easy’dataset with 6-DoF pose ground truth from a Vicon motion capture system is applied.Compared with KITTI dataset,the EuRoc UAV dataset suffers from greater vibration duringflying on trajectory.The typical image and IMU measurements are shown in Figs.7(b)and(c),respectively.
Similar to the experiment in KITTI dataset,the trajectory with great shock is chosen as the start point.The estimated trajectories of different methods are depicted in Fig.8(a).According to the ground truth(marked as black solid line),we canfind that the proposed I-MSCKF method(marked as blue dot dash line)can recover a more accurate trajectory than the MSCKF method(marked as red dash line).In addition,these estimated trajectories are projected to a 2D plane in Fig.8(b),and the results also illustrate that the proposed IMSCKF method is more close to the ground truth.
According to Eq.(45),the position RMSEs of different methods are compared with the ground truth.The results are shown in Table 2.

Fig.7 Typical dataset of EuRoc.

Fig.8 Trajectory comparisons with EuRoc dataset.

Table 2 RMSEs of different trajectories in EuRoc dataset.
The results in Table 2 also show that the proposed IMSCKF method is able to acquire superior performance to the MSCKF method.The reason may be that the start point of the navigation with severe vibration deteriorates the convergence of the MSCKF method,leading to the estimated trajectory drifted severely as time goes on.However,the proposed IMSCKF method can accomplish the initialization more effi-ciently and accurately,which will result in a more precise trajectory estimation regardless of the vibration at initial stage.
4.3.Case 3:Real experiment in indoor environment
In order to evaluate the performance of the proposed IMSCKF in different circumstances,real navigation experiments are carried out in indoor and outdoor environments.The experimental platform is shown in Fig.9,consisting of a consumer-grade monocular camera and IMU with rigid connection,and the corresponding coordinate frames are also depicted.The IMU is able to output the angular velocity and linearacceleration ata rateof100 Hz,and the camera can work at a frame rate of 30 Hz,with a resolution of 640 pixel×480 pixel.
In addition,a robust and convenient calibrated method30is used to evaluate the performance of the aforementioned consumer-grade IMU in this paper.It can calibrate the nonorthogonal sensitive error S,the scale factor K and the bias vector b of the IMU.According to the typical IMU measurement dataset,parameters of the accelerometer (Sa,Ka,ba)and the gyroscope (Sg,Kg,bg)can be obtained in Table 3,which can be used to compensate the original IMU measurements.
Different from aforementioned public datasets,our experiments encountered more challenges and irregular motion in extensive environments.Within the indoor scene,the experimental platform is carried on by the pedestrian in a random movement.Moreover,the lighting changes severely for different walking directions,and these would make the visual inertial navigation in trouble.
The typical experimental scenes in a large-scale GPS-denied indoor aisle are shown in Fig.10(a).The total length of the trajectory is about 400 m.The route is subjected to the sunshine from different directions.Therefore,the captured images may suffer from overexposure or underexposure at different positions.As shown in Fig.10(a),the intensity of typical images changes dramatically to each other.Coupled with the captured images,IMU measurements are also obtained synchronously,and the corresponding angular velocity and linear acceleration from IMU measurements are also depicted in Fig.10(b).
To illustrate the robustness of the proposed I-MSCKF method,the walking trajectory is suffered from a 180°sharp turn.In addition,given the different performance between the two methods,the vibration is performed intentionally at the initial stage,as the zoom features shown in Fig.11.According to the captured images and IMU measurements,the trajectory is estimated by the proposed I-MSCKF method,as the red solid line shows.The result of the MSCKF is depicted with blue dash line.These two trajectories are illustrated on the Google map.Although there is no ground truth,the tendency of the large scale aisle can also demonstrate the performance of different methods.

Fig.9 Monocularvision inertialnavigation experimental platform.

Table 3 Parameters of accelerometer and gyroscope in IMU.

Fig.10 Dataset obtained from indoor environment.
It is obvious tofind that the proposed I-MSCKF method has high consistency with the reference path(as the tendency of the coordinate line shows in Fig.11)along the building.However,due to the suffering from some shock at initial stage,the initialization of the MSCKF method is not robust and accurate enough,which makes the estimated trajectory far away to the reference path,by stretching out of the building.These results show that the proposed I-MSCKF method is qualified with a higher robustness and accuracy for monocular visual inertial navigation.

Fig.11 Comparison of trajectories in indoor environment.
4.4.Case 4:Real experiment in outdoor environment
Another experiment is performed in an outdoor environment with a closed loop,and the length of the total trajectory is about 800 m.The typical captured images are shown in Fig.12(a),and moving objects and illumination variation occur during the movement.The experimental platform for the outdoor scene is carried on a bike,which also results influctuations during the dataset capturing.Therefore,the IMU measurements of outdoor environment change more intensely than those of indoor environment,as shown in Fig.12(b),which also imposes more challenges to the visual inertial navigation.
With captured images and IMU measurements,the trajectories can be estimated by the MSCKF and I-MSCKF method,respectively(shown in Fig.13).As a closed-loop trajectory,ideally,the start point and the end point of the trajectory should coincide with each other.Thus,the distance between start and end point can be used to evaluate the performance of different navigation methods.Similar to other experiments,some shock is applied within the initial stage,as the enlarged view shows in Fig.13.It is easy tofind that the proposed I-MSCKF method can obtain a small closed-loop error(as marked by red solid line)with about 5.87 m.At the same time,for the MSCKF method,with the sensitivity to the initial condition,the closed-loop error is up to 29.12 m,which is about 5 times to that using the proposed I-MSCKF method.Therefore,the experimental result in the outdoor environment also shows that the I-MSCKF method can achieve superior performance to the MSCKF method.
4.5.Results and discussion
Monocular visual inertial navigation is nonlinear,and to properly fuse the monocular image and IMU measurements,a rapid and robust initialization is needed to bootstrap the integrated navigation system.In order to demonstrate the proposed I-MSCKF method, different qualitative and quantitative experiments are carried out.Thanks for the public dataset KITTI and EuRoc with accurate ground truths,comparative analyses are executed and the experimental results show the superior performance of the proposed method.Moreover,in order to verify the adaptability and universality of the I-MSCKF,other real experiments with consumergrade sensor module is tested both indoor and outdoor.Experimental results also indicate that the proposed I-MSCKF can bootstrap the monocular visual inertial navigation system more accurately and robustly than MSCKF.

Fig.12 Dataset obtained from outdoor environment.

Fig.13 Comparison of trajectories in outdoor closed-loop scene.
Ideally,as a visual inertial navigation system,the Earth rotation should be considered for an accurate integrated navigation performance.However,the aim of the proposed IMSCKF in the paper is to provide 6-DoF pose for daily applications,and thus the consumer-grade IMU is applied in our visual inertial navigation.The low-cost IMU has turn-on biases larger than Earth’s rotation rate(approximately 15 degree/hour or 1 rotation per day),meaning that the measured effects of the Earth’s rotation are small enough compared to the gyroscope accuracy.Thus,the influence of the Earth’s rotation is not included in the IMU kinematics within the paper.
In addition,given the integrated navigation by combining the monocular camera and IMU,the inertial propagation provides process model,while the measurement process is carried out by minimizing the re-projection error of visual features within a sliding window.Thus,the accuracy of the inertial navigation plays an important role for subsequent measurement update strategies.If a higher accurate inertial navigation is acquired,a more stable measurement update can be expected in the visual inertial navigation system.Thus,the quantitative comparison of different inertial navigation systems within the visual inertial navigation will be worth to do further research.Due to the limitation of experimental equipment,this comparison is not covered in this paper.However,according to experiments with different consumer-grade IMUs above,the results demonstrate that the proposed I-MSCKF can obtain reliable and improved navigation performance with different IMUs.
5.Conclusions
(1)The proposed I-MSCKF method for monocular visual inertial navigation is able to estimate the 6-DoF egomotion of the UAV or other mobile devices.The experimental results demonstrate that the I-MSCKF method owns greater robustness and accuracy than the MSCKF method.
(2)To alleviate the initial demands of the MSCKF method,a trifocal tensor based I-MSCKF method is proposed,which can reduce the initial requirements within only three successive images.Moreover,the initial pose estimation framework maintains a consistency with the MSCKF.Thus,the robustness and adaptability of the monocular visual inertial navigation can be improved.
(3)Attentions are also paid to the initial accuracy for visual inertial navigation,and the sigma-pointfilter is used instead of the EKF at the initial stage,which can achieve superiorposeestimationsofthenonlinearsystemwiththe third order of the Taylor series expansion.Thus,the subsequent navigation accuracy can also be improved.
(4)Finally,the extensive experimental results demonstrate that,even under some challenging initial conditions,the proposed I-MSCKF has better performance than the MSCKF.
Acknowledgements
The authors gratefully acknowledge the supports of the Beijing Key Laboratory of Digital Design&Manufacture,the Academic Excellence Foundation of Beihang University for Ph.D.Students,and the MIIT(Ministry of Industry and Information Technology)Key Laboratory of Smart Manufacturing for High-end Aerospace Products.
1.Goh ST,Abdelkhalik O,Zekavat SA.A weighted measurement fusion Kalmanfilter implementation for UAV navigation.Aerosp Sci Technol2013;28(1):315–23.
2.Tang L,Yang S,Cheng N,Li Q.Toward autonomous navigation using an RGB-D camera forflight in unknown indoor environments.Proceedings of 2014 IEEE Chinese guidance,navigation and control conference;2014 Aug 8–10;Yantai,China.Piscataway:IEEE Press;2014.p.2007–12.
3.Santoso F,Garratt MA,Anavatti SG.Visual-inertial navigation systems for aerial robotics:Sensor fusion and technology.IEEE T Autom Sci Eng2017;14(1):260–75.
4.Lu Y,Song D.Visual navigation using heterogeneous landmarks and unsupervised geometric constraints.IEEE T Robot2015;31(3):736–49.
5.Marchand E,Uchiyama H,Spindler F.Pose estimation for augmented reality:A hands-on survey.IEEE T Vis Comput Gr2016;22(12):2633–51.
6.Liu W,Ma X,Li X,Chen L,Zhang Y,Li XD,et al.Highprecision pose measurement method in wind tunnels based on laser-aided vision technology.ChinJAeronaut2015;28(4):1121–30.
7.Zhou H,Tao Z.A vision-based navigation approach with multiple radial shape marks for indoor aircraft locating.Chin J Aeronaut2014;27(1):76–84.
8.Wendel J,Meister O,Schlaile C,Trommer GF.An integrated GPS/MEMS-IMU navigation system for an autonomous helicopter.Aerosp Sci Technol2006;10(6):527–33.
9.Jeremy M,Max B,Sara S,Larry M,Matt M.Real-time pose estimation of a dynamic quadruped in GPS-denied environments for 24-hour operation.Int J Robot Res2016;35(6):631–53.
10.Zhu N,Zhao H,Feng W,Wang Z.A novel particlefilter approach for indoor positioning by fusing WiFi and inertial sensors.Chin J Aeronaut2015;28(6):1725–34.
11.Hesch J,Kottas DG,Bowman SL,Roumeliotis SI.Consistency analysis and improvement of vision-aided inertial navigation.IEEE T Robot2014;30(1):158–76.
12.Leutenegger S,Lynen S,Bosse M,Siegwart R,Furgale P.Keyframe-based visual–inertial odometry using nonlinear optimization.Int J Robot Res2015;34(3):314–34.
13.Lange S,Sunderhauf N,Protzel P.Incremental smoothing vsfiltering for sensor fusion on an indoor UAV.Proceedings of 2013 IEEE international conference on robotics and automation;2013 May 6–10;Karlsruhe,Germany.Piscataway:IEEE Press;2013.p.1773–8.
14.Wang C,Wang T,Liang J,Chen Y,Wu Y.Monocular vision and IMU based navigation for a small unmanned helicopter.Proceedings of 2012 7th IEEE conference on industrial electronics and application;2012 Jul 18–20;Singapore.Piscataway:IEEE Press;2012.p.1694–9.
15.Weiss S,Siegwart R.Real-time metric state estimation for modular vision-inertial systems.Proceedings of 2011 IEEE international conference on robotics and automation;2011 May 9–13;Shanghai,China.Piscataway:IEEE Press;2011.p.4531–7.
16.Mourikis AI,Roumeliotis SI.A multi-state constraint Kalmanfilter for vision-aided inertial navigation.Proceedings of 2007 IEEE international conference on robotics and automation;2007 Apr 10–14;Rome,Italy.Piscataway:IEEE Press;2007.p.3565–72.
17.Kelly J,Sukhatme GS.Visual-inertial sensor fusion:Localization,mapping and sensor-to-sensor self-calibration.Int J Robot Res2011;30(1):56–79.
18.Forster C,Pizzoli M,Scaramuzza D.SVO:Fast semi-directmonocular visual odometry.Proceedings of 2014 IEEE international conference on robotics and automation;2014 May 31–Jun 7;Hong Kong,China.Piscataway:IEEE Press;2014.p.15–22.
19.Mur-Artal R,Montiel JMM,Tardos JD.ORB-SLAM:A versatile and accurate monocular SLAM system.IEEE T Robot2015;31(5):1147–63.
20.Li M,Mourikis AI.Improving the accuracy of EKF-based visualinertial odometry.Proceedings of 2012 IEEE international conference on robotics and automation;2012 May 14–18;Minnesota,USA.Piscataway:IEEE Press;2012.p.828–35.
21.Li M,Mourikis AI.3-D motion estimation and online temporal calibration for camera-IMU systems.Proceedings of 2013 IEEE international conference on robotics and automation;2013 May 6–10;Karlsruhe,Germany.Piscataway:IEEE Press;2013.p.5689–96.
22.Gui J,Gu D.A direct visual-inertial sensor fusion approach in multi-state constraint Kalmanfilter.Proceedings of the 34thChinese control conference;2015 Jul 28–30;Hangzhou,China.Piscataway:IEEE Press;2015.p.6105–10.
23.Yang Z,Shen S.Monocular visual-inertial state estimation with online initialization and camera-IMU extrinsic calibration.IEEE T Autom Sci Eng2017;14(1):39–51.
24.Trawny N,Roumeliotis S.Indirect Kalmanfilter for 3D attitude estimation.Minneapolis:University of Minnesota;2005 Report No.:2005-002.
25.Civera J,Davison AJ,Montiel JMM.Inverse depth parametrization for monocular SLAM.IEEE T Robot2008;24(5):932–45.
26.Hartley R,Zisserman A.Multiple view geometry in computer vision.2nd ed.Cambridge:Cambridge University Press;2008.p.365–83.
27.Sarkka S.On unscented Kalmanfiltering for state estimation of continuous-time nonlinear systems.IEEE T Automat Contr2007;52(9):1631–41.
28.Geiger A,Lenz P,Stiller C,Urtasun R.Vision meets robotics:The KITTI dataset.Int J Robot Res2013;32(11):1231–7.
29.Burri M,Nikolic J,Gohl P,Schneider T,Rehder J,Omari S,et al.The EuRoC micro aerial vehicle datasets.Int J Robot Res2016;35(10):1157–63.
30.Tedaldi D,Pretto A,Menegatti E.A robust and easy to implement method for IMU calibration without external equipment.Proceedings of 2014 IEEE international conference on robotics and automation;2014 May 31–Jun 7;Hong Kong,China.Piscataway:IEEE Press;2014.p.3042–9.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Guide for Authors
- An aviation oxygen supply system based on a mechanical ventilation model
- Influence of TiB2particles on machinability and machining parameter optimization of TiB2/Al MMCs
- An investigation on adaptively machining the leading and tailing edges of an SPF/DB titanium hollow blade using free-form deformation
- Analysis of the cylinder block tilting inertia moment and its effect on the performance of high-speed electro-hydrostatic actuator pumps of aircraft
- A direct position determination method with combined TDOA and FDOA based on particlefilter
