基于质点模型的多智能体遗传算法

张鑫+许峰

摘要：针对传统遗传算法优化高维函数效率不高的问题，借鉴质点间相互作用机制，提出了一种基于质点模型的多智能体遗传算法。基本思想是：定义质点的质量表示智能体的历史活动信息及具有的能量，通过质点间引力作用的特点，不断提高智能体的自学习能力和自身的能量。该算法具有较高的优化效率，特别适合高维函数的优化。

关键词：遗传算法；多智能体；质点模型；算法效率

DOIDOI：10.11907/rjdk.172216

中图分类号：TP312

文献标识码：A文章编号文章编号：16727800（2018）001008104

Abstract：A multi agent genetic algorithm based on particle model is proposed for the traditional genetic algorithm， which is prone to search efficiency is not high and precocious. The quality of the defined particle represents the historical activity information of the agent and its energy. Through the interaction between the particles， the selflearning ability and the energy of the agent are improved. The algorithm has higher optimization efficiency and is especially suitable for the optimization of highdimensional functions.

Key Words：genetic algorithm； multiagent； particle model； algorithm efficiency

0引言

遺传算法是经过模拟生物在自然界的进化而产生的一种优化算法，应用广泛。但传统遗传算法在优化高维甚至超高维函数时，效率不高，从而使其实用性大打折扣。基于智能体（Agent）的优化方法已广泛应用于计算科学的各个领域，它们通过推理、学习、协作和协商能力感知环境并做出反应，可对复杂问题有效求解。多智能体系统的分布式并行布局有利于防止遗传算法早熟，而智能体自身的邻域结构有利于提高种群的局部搜索能力，由此产生了很多改进的遗传算法[1]。钟伟才[24]等将智能体与遗传算法相结合，提出了多智能体进化算法，提升了算法的求解精度，但是消耗了大量时间；文献[5]提出的协同进化遗传算法收敛速度快，但它破坏了变量之间的相关性，导致搜索解的质量差；文献[6]把智能体的动态链式网络布局加入到遗传算法中，削减了次优个体过早获得“顶端优势”，防止早熟，可以保持种群多样性；文献[7]把均匀设计方法加入到智能遗传算法中，在某些方面避免了局部最优；文献[8]将差分进化算子结合到多智能体遗传算法上，提升了智能体的换代速度；文献[9]提出了交互式多智能遗传算法，增强了算法的全局收敛能力和局部搜索能力；文献[10]把多种群的概念加入到遗传算法中，考虑了种群数量对收敛速率的影响；文献[11]创建了包括“智能体、环境、交互式规则”3个重要概念的AER模型，有效解决了多达7 000个皇后的问题和一些大规模着色问题；文献[12]把均匀设计的思路、多智能体系统以及遗传算法相结合，提出了高维多峰函数算法，拥有很好的全局搜索能力和较快的收敛速率。上述各种改进算法都在某些方面提高了算法的寻优能力和收敛速度。

为了提高遗传算法高维优化的效率，本文将“理想化模型——质点”的思想引入到多智能体遗传算法中，提出了一种基于质点模型的多智能体遗传算法。算法采用多智能体相互作用的演化结构，各智能体分别与其它智能体

产生引力作用，通过矢量合成得到各智能体合力，相互进行比较、竞争、合作及自学习，实现自身能量的增加，向着群体最优的方向移动，各智能体定期通过引力作用操作进行信息交互。

1质点模型的多智能体遗传算法

1.1质点模型

任何物体都具有尺寸、形状、质量和空间特性，这些属性混合在一起就很难确定物体的位置和研究对象的运动。假设物体是在一个很大的空间内，自身的体积远远小于空间范围，则确定物体在空间的位置时，其自身因素对结果影响很小，这时就可以忽略物体的尺寸和形状等特性，用一个具有质量的点去代替实际物体，在物理学中称为质点。质点是科学概括的产物，是一个理想化模型，事实上不存在。质点并不是凭空想象出来的，它与实际物体有着密切关系，这种关系表现在：质点是以实际物体为基础建立起来的，对质点的描述和探究的结果能够代替实际结果。

1.2智能体

1.2.1智能体定义

将环境中的每个个体看作一个智能体，它具有自身的特征，可以了解周围环境，也可以作用和改善环境。Agent具有3种基本状态：信念、期望和意图，分别代表知识、水平和目标。Agent具有强大的智能特征，以固定的方式响应环境的要求和变化，并且能根据自身状态和学习的环境信息主动决定和控制状态以及行为。Agent在了解环境并作出反应的同时，展示出应变行为，采取积极行动实现目标。

1.2.2智能体能量

一个智能体相当于质点模型多智能体遗传算法中的一个质点，表示待优化函数的一个可能解。用质点的质量表示智能体的能量，能量越大，引力越强；反之，则弱。当引力较大时，自身的能量会不断增加，而引力较小者将被淘汰。在求整体最优结果问题中，它的能量等于目标函数的结果。智能体的目的就是在满足运行条件的情况下尽量增加其能量。endprint

1.2.3多智能体系统

与现实中的群体相同，Agent经常不是独立存在的，在环境中会有许多Agent生存，构成一个大的群体。Agent不仅可以自主运行，还能和其它Agent相互协作，并能在遇到矛盾时通过协商消解冲突，随着环境的不断变化充实自身的学问和能力，提升整个系统的智能化和可靠性。这些Agent相互协作，达到共同的目标，这种系统叫作多智能体系统。就像人类合作的能力要远大于个体一样，MAS比单个Agent有更高的智能性和更强的解决问题能力。

多智能体模型主要针对系统内共同目标的实现，为多个智能体制定共同的规划。每个Agent都有自己的求解目标，并且每个Agent都考虑其它Agent的行为和约束，并进行独立规划，称为局部规划。各个Agent以通信的方式进行协调，实现所有Agent都接受的全局规划。

1.2.4智能体区域

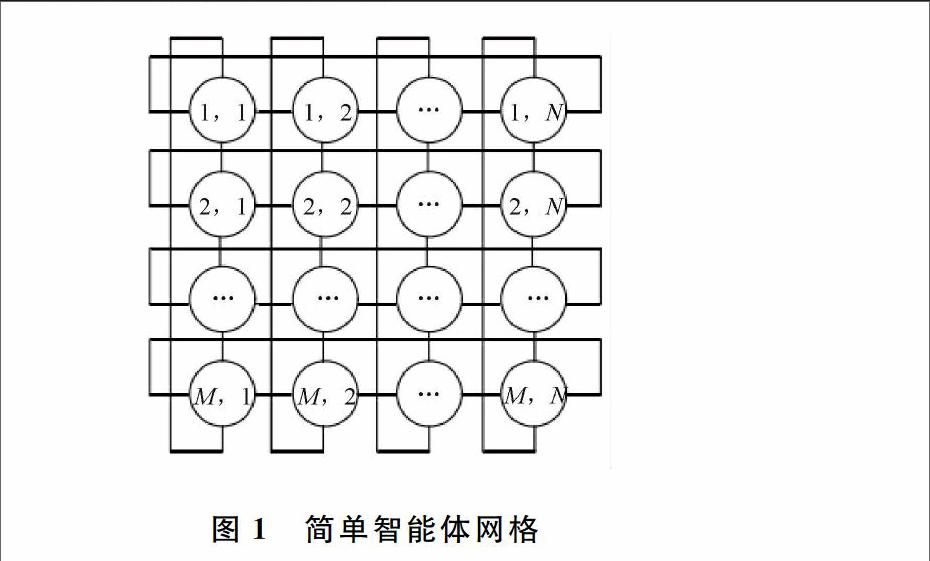
简单MAS的生存环境由一个网格组成，群体内共有N×M个Agent，稱为简单智能体网格，记为A。每个Agent固定在一个位置上，第p行第q列的Agent表示为Ap，q， p=1，2，…，N；q=1，2，…，M；则智能体Ap，q的邻域为Neighborsp，q={Ap1，q， Ap2，q，Ap，q1， Ap，q2}，p=1，2，…，N； q=1，2，…，M；分别是与Agent直接相连的上下左右的Agent，其中每个Agent只能与相邻的Agent发生相互作用，无法与远端以及其他区域的智能体发生相互作用，智能体网格表示成图1的形式。每个圆圈为一个智能体，圆圈中的数字代表智能体在网格中的位置，相连的Agent可以直接发生相互作用。

1.3智能体的行为算子

1.3.1竞争算子

首先，找出智能体Ap，q=（a1，a2，…，an）的邻域内能量最大的智能体Amaxp，q=（m1，m2，…，mn），如果Ap，q的能量大于Amaxp，q的能量，则继续保留在网格上；否则，将被Amaxp，q替代，体现了智能体之间的竞争。

1.3.2合作算子

除了竞争，Agent之间还有合作关系。合作算子将利用彼此的信息去实现不同的Agent合作。算术交叉是一种常用方法，其优点是收敛速度快、性能稳定，但是只采用该算子时，产生的个体数值特性比较接近，对优化不利，会在该区域内过早收敛。因此，以增大选择空间、加快进化速度为目的，采用混合交叉的方法得到新的Agent。

1.3.3变异算子

保留在网格上的智能体以概率P1进行变异，Agent利用自身知识获得能量增加。以概率P1选取要进行变异的Agent a=（a1，a2，…，al，am，an，…，ak），随机选择其中的两个分量al和an进行变异，变异产生新的Agent a′=（a1，a2，…，a′l，am，a′n，…，ak）。

1.3.4自学习算子

Agent不仅可以在局部环境与其它Agent进行竞争与合作，还能够通过自身所拥有的知识进行自学习。生存在网格上的Agent以概率P2进行自学习操作，进一步提高求解问题的能力，使算法逐渐收敛。

1.4算法原理与步骤

1.4.1算法原理

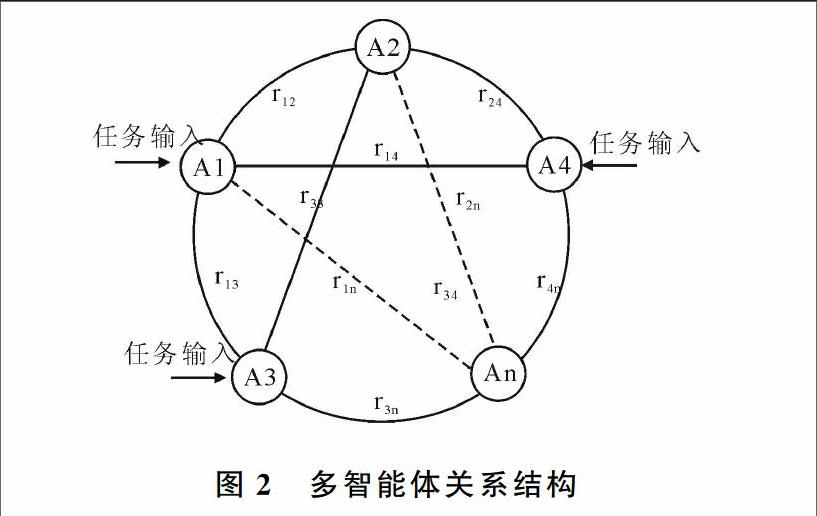
多Agent系统模型应当将系统内的个体和环境作为一个整体来描述，包含多个智能体的系统用关系型网络结构描述，如图2所示。在图中，有n个智能体，每个智能体都可以接受环境的任务输入。任意两个Agent之间连线上的字母rij代表它们之间的万有引力。针对不同系统中Agent之间关系的复杂程度，在关系型网络结构模型中，可以通过调整距离的大小对系统模型进行精确描述。

图2多智能体关系结构

在实际应用中，有时无法精确描述Agent的关系，于是引入万有引力概念，提出一种更实用的质点模型。各智能体之间引力的大小F=GMmR2，表示Agent之间的对立和合作关系以及相互影响程度的大小。其中G表示万有引力常量，M、m表示两个智能体的能量，R表示两个智能体之间的距离。邻域内任何两个智能体可以计算出它们之间引力的大小。通过比较引力大小，保留优秀个体。

在质点模型多智能体遗传算法中，每个Agent就是一个质点，Agent的数量就是算法的群体规模。每个质点的邻域就是每个Agent的邻域，智能体网格中能量最大的Agent就是群体中的最优个体。在算法中，通过竞争算子和合作算子以及变异算子，分别实现Agent的竞争、合作、更新行为，通过自学习算子实现智能体利用自身知识。结合质点模型，与全局最优的Agent进行信息同享，并根据自身经验来修正Agent的行动策略，使其可以更快、更精确地收敛到全局最优解。每个Agent利用固有的特征以及与邻域内其它Agent的相互作用，再通过质点之间的引力算法的更新机制完成种群更替，实现每一代的进化。

1.4.2算法步骤

①设置算法参数，构造智能体环境；②初始化各质点位置，并计算每个质点的能量，找出全局最优智能体Ag；③对每个质点执行邻域竞争算子；④对每个质点执行任意合作算子；⑤每个质点通过变异算子更新自己的状态，并更新全局最优智能体Ag的状态；⑥对全局最优质点执行自学习算子；⑦检查终止条件，若条件成立，输出最优解，算法终止；否则转第③步。

2.2数值实验结果

算法计算量主要体现在函数评价次数上。表1给出了优化10 000维函数时，AEA和MAGA评价次数和O（nα）的逼近结果。考虑到运算的随机性，给出的是20次运算的平均结果。

为了直观、形象地显示函数维数对AEA和MAGA

的影响，图3给出了这两种方法的平均函数评价次数随n的变化，及用函数O（nα）逼近评价次数的结果。

从表1及图3中的O（nα）逼近结果来看，10个测试函数中有9个AEA的复杂度都劣于O（n），仅有f3的复杂endprint

度为O（n0.79）。而对于MAGA，除f2外均优于O（n）。在MAGA的逼近结果中，较差的是f1和f6，分别为O（n0.78）和O（n0.79），f3和f7～f10的复杂度仅为O（n0.1）左右。由此可见，基于质点模型的多智能体遗传算法具有极低的复杂度，特别适宜于高维甚至超高维函数的优化。

3结语

本文将质点模型与多智能体遗传算法相结合，提出了一种基于质点模型的多智能体遗传算法。该算法将智能体的竞争、合作、变异以及自学习行为与质点间的引力关系相结合，提高了环境适应力。数值实验表明，与其它改进的遗传算法相比，该算法在进行高维函数优化时具有突出的搜索效率，特别适用于高维或超高维函数的优化。

参考文献：

[1]SRINIVAS M， PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems， Man and Cybernetics，1994，24（4）：656667.

[2]钟伟才，薛明志，刘静.多智能体遗传算法用于超高维函数优化[J].自然科学进展，2003，13（10）：10781083.

[3]ZHONG W C， LIU J， XUE M Z， et al. A multiagent genetic algorithm for global numerical optimization[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B： Cybernetics，2004，34（2）：11281141.

[4]LIU J， ZHONG W C， JIAO L C. A multiagent evolutionary algorithm for constraint satisfaction problems[J]. IEEE Transactions on Systems， Man， and Cybernetics， Part B： Cybernetics，2006，36（1）：11281141.

[5]孙晓燕，巩敦卫.变种群规模合作型协同进化遗传算法及其在优化中的应用[J].控制与决策，2004，19（12）：14371440.

[6]ZENG X P， LI Y M， JIAN Q. A dynamic chainlike agent genetic algorithm for global numerical optimization and feature selection [J].Neurocomputing，2009，72（46）：12141228.

[7]梁昌勇，陆青，张恩桥.基于均匀设计的多智能体遗传算法研究[J].系统工程学报，2009，24（1）：109113.

[8]何大阔，高广宇，王福利.多智能体差分进化算法[J].控制与决策，2011，26（7）：962972.

[9]黄永青，陆青，梁昌勇.交互式多智能体进化算法及其应用[J].系统仿真学报，2006，18（7）：20302055.

[10]姚志红，赵国文.多种群变换遗传算法及其在优化调度中的应用[J].控制理论与应用，2001，18（7）： 882886.

[11]韩靖，蔡庆生.AER模型中的智能涌现[J].模式识别与人工智能，2002，15（2）：134142.

[12]梁昌勇，陸青，张恩桥.基于均匀设计的多智能体遗传算法研究[J].系统工程学报，2009，24（1）：109 113.

[13]焦李成，刘静，钟伟才.协同进化计算与多智能体系统[M].北京：科学出版社，2006.

[14]PAN Z， KANG L S. An adaptive evolutionary algorithm for numerical optimization[J]. In： Simulated Evolution and Learning， Lecture Notes in Artificial Intelligence. Heidelberg： SpringerVerlag，1997（1285）：2734.

（责任编辑：杜能钢）endprint