具有Beddington-DeAngelis发生率的随机SIS传染病模型的定性分析

， ，，同迁

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

1 引言与模型建立

传染病是人类的宿敌,人类的历史充斥着与传染病的斗争。传染病给人类造成了巨大的灾难,天花、霍乱、艾滋病等让人闻之色变[1]。为了控制传染病,研究者建立了很多数学模型去研究传染病的传播动力学[2-6]。在传染病动力学中,重要的数学模型是KERMACK和MCKENDRICK在1927年提出的仓室模型[7]。在这个仓室模型中,人们被分为三个相互隔离的仓室：易感者仓室“S”,染病者仓室“I”,以及恢复者或移出者仓室“R”。在模型中,易感者可以通过与染病者接触而转化为染病者,而染病者可以通过治疗转化为恢复者或移出者,并获得永久的免疫能力,这个模型被称之为SIR模型。然而有些疾病并不符合SIR模型,比如流行感冒,患者经过治疗后,不能获得永久免疫力,还有再次感染该种疾病的可能。这样建立的模型被称为SIS模型[8]。文献[7-8]中采用了常见的非线性传染率-双线性传染率βSI。研究者还研究了很多其他类型的非线性传染率[9-11]。

众所周知,随机噪声因素在传染病的传播中起着重要作用,因此,许多学者对传染病模型随机性的影响进行了研究[12-13],不同的随机干扰方法被引入到传染病模型当中,并取得了很好的结果[14-23]。 基于以上文献分析,考虑传染率受到随机白噪声干扰即β→σdB(t)及人口输入、因病死亡率等因素,建立了一类具有Beddington-DeAngelis发生率的随机型SIS传染病动力学模型：

(1.1)

这里A表示人口的输入率(包括人口的出生和迁入),a和b是测量抑制效果的参数,α表示因病死亡率,σ2是噪声强度,B(t)是标准布朗运动。

2 预备知识

定义2.1对于模型(1.1),

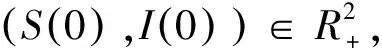
几乎处处成立。

引理2.4(伊藤公式) 设x(t),t≥0是方程dx(t)=f(x(t),t)dt+g(x(t),t)dB(t),0≤t<∞的解,V∈C2,1(Rn×R+;R)。则函数V(x(t),t)仍是一伊藤过程,具有如下随机微分：

dV(x(t),t)= [Vt(x(t),t)+Vx(x(t),t)f(x(t),t)

上式称为伊藤公式。

3 模型的分析

3.1 确定型SIS传染病模型的定性分析

首先我们考虑确定性SIS传染病模型：

(3.1)

下面考虑模型(3.1)的平衡点的稳定性。

模型在疾病消除平衡点E0:(S0,0)处的雅可比矩阵为

显然,若R<1，则疾病消除平衡点E0:(S0,0)是局部稳定的; 若R>1，则疾病消除平衡点E0:(S0,0)是不稳定的。

其特征方程为

λ2+(a11+a22)λ+a11a22-a21a12=0,

其中

显然

而

从而特征根总有负实部,故若存在疾病平衡点E:(S*,I*)，则疾病平衡点必是局部稳定的。因此得到如下定理。

定理3.1.2对于模型(3.1),

1) R<1，疾病消除平衡点E0:(S0,0)是局部稳定的;

3.2 随机SIS传染病模型(1.3)的定性分析

定义

证明：设初值为(S(0),I(0))∈Ω。设(S(t),I(t))是模型(1.1)的具有初值的解。在模型(1.1)的第二个方程中应用伊藤公式得

(3.2)

两边在[0,t]上积分得

(3.3)

考虑二次函数

(3.4)

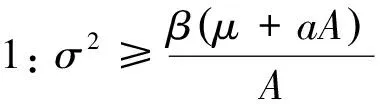
从式子(3.3)可得

(3.5)

(3.5)式两边同时除以t(t>0)，得

(3.6)

由引理2.3知

式子(3.6)两边同时取上极限得

(3.7)

(3.7)式两边同时取上极限得

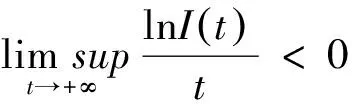
“云计算”是IT技术的一个主流发展方向，“云计算”的普及意味着快捷的空间共享、信息资源共享，也意味着不再需要电脑主机，只要有显示器或具有相当于显示器功能的设备、再加上网络，就可以开展工作。网络化的系统，应允许从电脑端、以及移动端登录。基于BIM的各项技术需与“云计算”相结合。

(3.8)

在上式中令ε→0，得到

(3.9)

另一方面,由引理2.2，可以得到

(3.10)

从而由方程(3.9)与(3.10)知

几乎处处成立,证毕。

定理3.2.2若R*>1，则模型的疾病I(t)是持久的,并且有

证明：对式(1.1)两端同时求从0到t求积分,并两边同时除以t(>0)，可以得到

接着可以得到

(3.11)

(3.12)

上式从0到t求积分,然后方程两边同时除以t(>0)得

(3.13)

不等式(3.13)可以写成

(3.14)

对(3.14)式两端取下极限：

图1 模型(1.3)的时间序列图

证毕。

4 数值模拟

为了验证得到的理论结果,给出一些数值模拟。取基本参数为

A=0.2,μ=0.4,β=2,r=0.2,α=0.1,a=1,b=1。

计算知R=0.952 4<1，根据定理3.2.1,模型的疾病消除平衡点E0:(0.5,0)是局部稳定的(图1)。若增大人口的输入率A=0.5，此时R=1.587 3>1，根据定理3.2.2知,模型的疾病平衡点E*:(0.752 7，0.397 8)是局部稳定的(图2)。

下面在持久的系统上考虑随机干扰的影响。首先,令σ=1.9，满足定理3.2.1的第一个条件,于是疾病最终消除(图3)。其次，令σ=1.7，此时,R*=0.950 2<1， 满足定理3.2.1的第二个条件,由定理3.2.1知,疾病最终消除(图4)。若令σ=0.3，经过计算,R*=1.567 5>1，由定理3.2.2知,疾病是持久的(图5)。

图2 模型(1.3)的时间序列图

图3 确定性模型和随机模型动力学行为对比

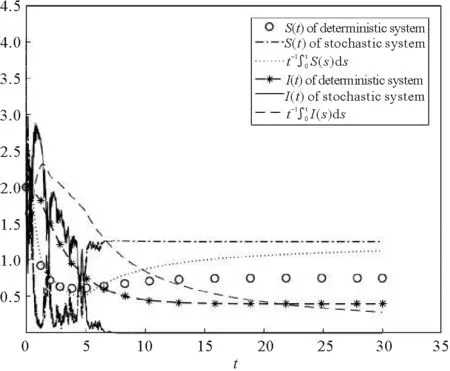
图4 确定性模型和随机模型动力学行为对比

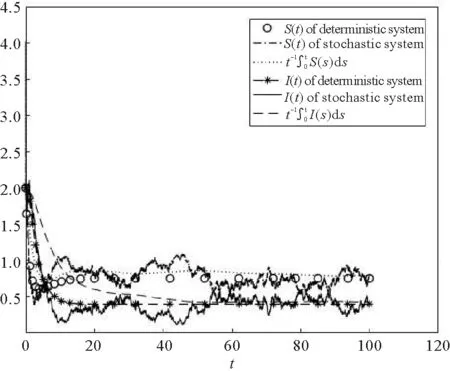
图5 确定性模型和随机模型动力学行为对比

5 结论

[1]HAMER W H.Epidemic disease in England,Lancet[M].Bedford:Bedford Press,1906:733-739.

[2]BRAUER F,CASTILLO-CHAVEZ C.Mathematical models in population biology and epidemiology[M].2nd Edition.New York:Springer,2012.

[3]MINCHIN E A.The prevention of malaria[J].Indian Medical Gazette,1911,46(2):64-66.

[4]MAY R M,ANDERSON R M,MCLEAN A R.Possible demographic consequences of HIV/AIDS epidemics:I.Assuming HIV infection always leads to AIDS[J].Mathematical Biosciences,1988,90(1):475-505.

[5]ANDERSON R M,MAY R M.Infectious diseases of human:Dynamics and control[M].Oxford:Oxford University Press,1992.

[6]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.

[7]KERMACK W O,MCKENDRICK A G.A contribution to the mathematical theory of epidemics[J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1927,115:700-721.

[8]KERMACK W O,MCKENDRICK A G.Contributions to the mathematical theory of epidemics:III.Further studies of the problem of endemicity[J].Bulletin of Mathematical Biology,1991,53(1):57-87.

[9]XU R,MA Z E.Global stability of a SIR epidemic model with nonlinear incidence rate and time delay[J].Nonlinear Analysis Real World Applications,2009,10(5):3175-3189.

[10]LIU W M,LEVIN S A,IWASA Y.Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models[J].Journal of Mathematical Biology,1986,23(2):187-204.

[11]RUAN S,WANG W.Dynamical behavior of an epidemic model with a nonlinear incidence rate[J].Journal of Differential Equations,2003,188(1):135-163.

[12]MAO X R.Stochastic differential equations and applications[M].2nd ed.Chichester:Horwood Publishing,2007.

[13]冯涛,孟新柱.一类捕食者染病的捕食者-食饵系统的随机动力学行为[J].山东科技大学学报(自然科学版),2017,36(1):99-110.

FENG Tao,MENG Xinzhu.Stochastic dynamics of a predator-prey system with disease in predator[J].Journal of Shandong University of Science and Technology (Natural Science),2017,36(1):99-110.

[14]ZHAO W C,LI J,ZHANG T Q,et al.Persistence and ergodicity of plant disease model with Markov conversion and impulsive toxicant input[J].Communications in Nonlinear Science and Numerical Simulation,2017,48:70-84.

[15]MENG X Z,ZHAO S N,FENG T,et al.Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis[J].Journal of Mathematical Analysis and Applications,2015,433(1):227-242.

[16]CHANG Z B,MENG X Z,LU X.Analysis of a novel stochastic SIRS epidemic model with two different saturated incidence rates[J].Physica A:Statistical Mechanics and its Applications,2017,472:103-116.

[17]MIAO A Q,ZHANG J,ZHANG T Q,et al.Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination[J].Computational and Mathematical Methods in Medicine,2017:4820183.

[18]MIAO A,WANG X,ZHANG T,et al.Dynamical analysis of a stochastic SIS epidemic model with nonlinear incidence rate and double epidemic hypothesis[J] Advances in Difference Equations,2017(1):226.

[19]LIU Q,JIANG D Q,SHI N Z,et al.Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence[J].Physica A:Statistical Mechanics and its Applications,2017,469:510-517.

[20]DU N H,NHU N N.Permanence and extinction of certain stochastic SIR models perturbed by a complex type of noises[J].Applied Mathematics Letters,2017,64:223-230.

[21]LI C G,PEI Y Z,LIANG X Y,et al.A stochastic toxoplasmosis spread model between cat and oocyst with jumps process[J].Communications in Mathematical Biology and Neuroscience,2016 :Article ID 18.

[22]BERETTA E,KOLMANOVSKII V,SHAIKHET L.Stability of epidemic model with time delays influenced by stochastic perturbations[J].Mathematics and Computers in Simulation,1998,45(3/4):269-277.

[23]LIU M,BAI C Z,WANG K.Asymptotic stability of a two-group stochastic SEIR model with infinite delays[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(10):3444-3453.