复数共轭运算的推广及应用
2018-01-31赵晓辉杨广武
赵晓辉,杨广武
(1.河北工程技术学院经济管理学院,河北 石家庄 050091;2.河北科技大学理学院,河北 石家庄 050018)
0 引言
复变函数中的共轭运算在数学领域及有关二维场等实际问题中有重要应用。但目前有关的研究中仅讨论了在有限运算情形下的共轭问题[1-2]。本文研究了各种极限情形中最重要的共轭运算,得到了相关的结果,并举例说明了其应用。
1 运算的推广及简单应用
在基础数学研究领域中关于数的运算的研究,尤其是关系到由有限到无限的飞跃,具有重要意义。为区别于侧重代数方面的讨论[3-4],本文讨论了共轭复数列、函数的极限及共轭运算在函数的连续性、可导、级数及复变函数的积分等方面的相关问题,进行了一定的推广[5-8],简列于下:
2)若f(z)=u+iv在z0=x0+iy0可导,则关于在处可导,且
此由定义可证。另若u,v在(x0,y0)可微,且满足Cauchy-Riemann偏微分方程组,可证u,-v在点(x0,-y0)关于x,-y亦然。
由和、积的共轭运算及1)可知
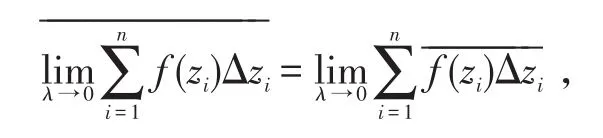
另外,若化为对坐标的曲线积分,则有
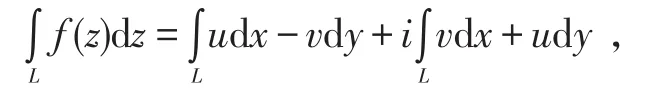
其中f(z)=u+iv,z=x+iy。
而
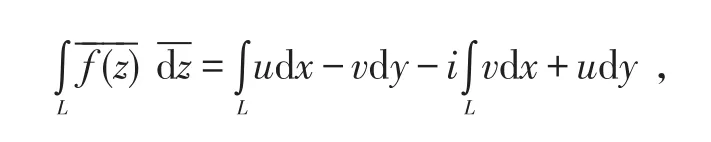
可知
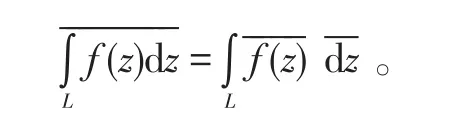
5)作为复数的共轭运算在积分、级数方面的应用举例
对于几何级数,假定||z<1,则有
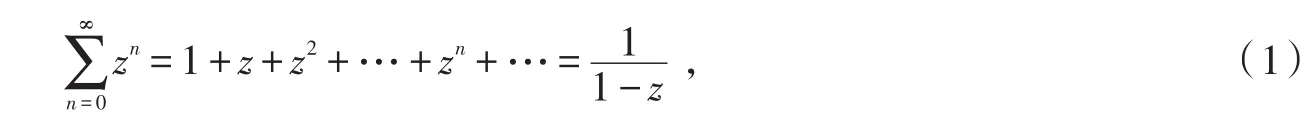
同时考虑
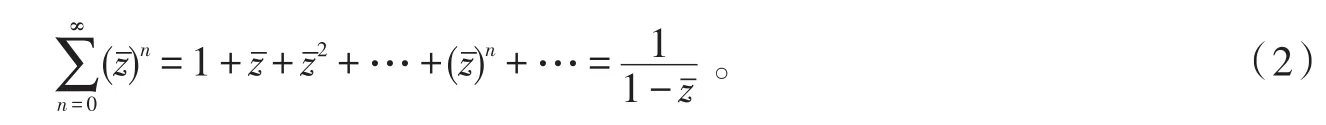
由复数的三角表示及棣莫夫定理知
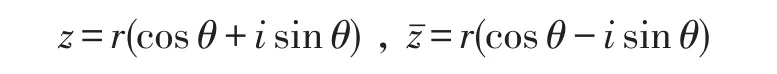
和
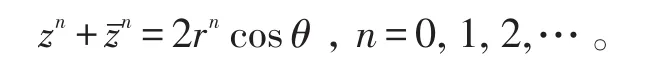
(1)、(2)式两边分别相加,有
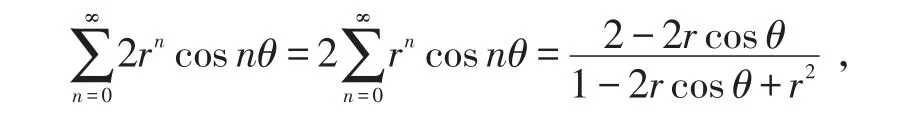
从而得到

同样,由(1)式减(2)式可得

级数(3)、(4)中既含有r,又含有θ,它们在有关级数理论的研究中有重要意义。
2 主要结果
Poisson积分公式在函数论、微分方程中有着重要应用[9],原证法主要有三种,此处给出一个新的证法。
定理(Poisson积分公式) 设复变函数f(z)=u+iv在圆内解析,在闭圆盘上连续,则当 0<r<R时,有

证明记Γ为圆周| |ς-z0=R。由柯西积分公式,有


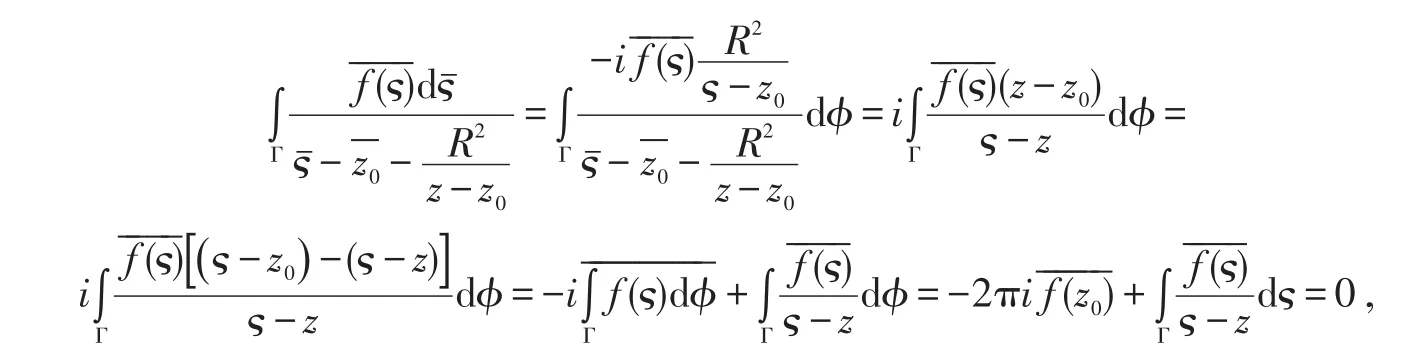


此处u(ς)=Ref(ς)。由(8)式以及有
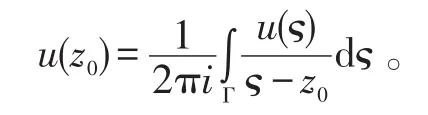
因此(8)式可改写为

这里,经计算知实常数C=Imf(z0)。
将z-z0=reiθ,z-z0=Reiθ代入(9)式,则有


故得
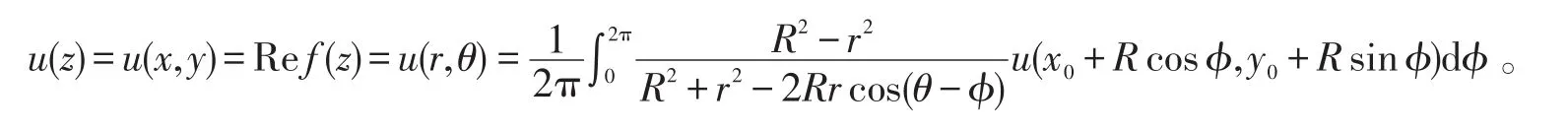
(References)
[1]乔治·波里亚,戈登·拉达.复变函数[M].路见可,余家,林玉波,等,译.北京:高等教育出版社,1985.
[2]胡文茜.复数运算的几何特征及实践研究[D].长沙:湖南师范大学,2016.
[3]王会珍.共轭积框架下复多项式矩阵的实表示[D].哈尔滨:哈尔滨工业大学,2013.
[4]焦腾腾.复数知识与数学研究[D].西安:西北大学,2016.
[5]李立珺.复数乘法运算的优化方法研究与实现[J].电子设计工程,2013,21(13):157-161.
[6]孟令彬.共轭复数的性质及应用[J].邢台师范高专学报,2000,15(2):74-77.
[7]李鸿仪.方程共轭复数解在实平面上的几何意义[J].上海第二工业大学学报,2006,23(3):177-187.
[8]WANG J.Bound the number of limit cycles bifurcating from center of polynomial Hamiltonian system via interval analysis[J].Chaos Solutions&Fractals,2016,87(6):30-38.
[9]R·柯朗,D·希尔伯特.数学物理方法[M].钱敏,郭敦仁,译.北京:科学出版社,1981.
