等壁温下超临界CO2于螺旋管内对流传热的数值模拟

顾 骞 余南阳



等壁温下超临界CO2于螺旋管内对流传热的数值模拟

顾 骞 余南阳

（西南交通大学机械工程学院 成都 610031）

在等壁温条件下，对超临界CO2于螺旋管内的对流传热进行了数值模拟。得出并分析了超临界CO2在螺旋管内对流换热过程中温度、流速和密度的分布情况，总结了螺旋管内超临界CO2的局部对流传热系数沿轴向角的变化规律，讨论了壁面温度的改变对螺旋管内局部对流传热系数的影响。研究结果表明：离心力的影响在整个对流传热过程均存在，浮升力的影响在流体离开拟临界区之前不能忽略；当轴向角≤1035°时，bottom母线上的最大，inner母线上的最小且最先达到峰值；局部对流传热系数的峰值会随壁面温度的增大而减小。

等壁温；螺旋管；超临界CO2；对流传热；数值模拟

0 引言

超临界CO2因其高效的换热特性以及无毒、无味、易于回收利用的特点，被广泛地应用于空调及热泵系统当中。由于超临界CO2在拟临界区，其比热、密度、粘度和热导率等热物性参数会发生剧烈变化，这使得其在管内的换热过程变得非常复杂。国内外学者对超临界CO2在管内的流动与传热特性开展了大量研究。Bruch等[1]对超临界CO2在管内被水冷却降温的过程进行了实验研究，分析了压力、质量流量的改变对传热系数、浮升力强度的影响。Tanimizu和Sadr[2]用三种常用的浮升力判据对超临界CO2在水平管内对流传热的浮升力程度进行了评估。徐轶君等[3-5]对超临界CO2在竖直圆管内的对流换热进行了实验研究，探究了压力、入口温度、流量等对换热的影响。饶政华和廖胜明[6-9]运用数值模拟的方法对超临界CO2在细微圆管、微通道气体冷却器和水平三角细微管中流动与换热进行了分析。杨传勇等[10,11]对超临界CO2在倾斜管内的对流传热过程进行了数值模拟，分析了管道倾斜角度对超临界CO2管内换热特性的影响。齐伟等[12]借助Matlab软件开发出了一种针对超临界流体在冷却管内对流传热问题的工程预测方法，并将通过该方法得到的计算结果与实验数据比较，证明了其方法的正确性。

以上研究主要都是针对超临界CO2在直管中的对流换热问题所展开的。螺旋管由于结构较为紧凑，有利于节省空间，提高换热效率，已成为输送传热流体介质的理想管路。在超临界CO2于螺旋管内的传热研究方面，Zhang等[13]对超临界CO2在竖直螺旋管内的混合对流传热过程进行了实验研究，分析了浮升力、离心力对传热的影响。李洪瑞等[14]通过数值模拟的方法探讨了超临界CO2在螺旋管内不同流向下的换热和压降变化。由于上述螺旋管内的传热研究所涉及的壁面工况均为等热通量条件，对等壁温条件下螺旋管内的流动传热研究还有待开展。因此，本文将通过CFD软件探究等壁温条件下超临界CO2在螺旋管内的流动及换热情况，对流体在管内的温度、密度、流速、浮升力和局部对流传热系数等情况展开分析和讨论，本文得出的结论对螺旋管式超临界压力换热设备的设计与优化具有一定的参考价值。

1 数理模型及求解方法

1.1 物理模型

螺旋管的几何模型如图1所示。模拟所用螺旋管具体尺寸为：螺旋管直径=9mm，螺旋曲率直径=283mm，螺距=32mm。超临界CO2在螺旋管内自下而上流动并被管壁加热。在图1中，以z轴作为螺旋管轴线，为轴向角，入口处=0，每增大360°，螺旋管就向上抬升一个螺距的高度。图中inner、outer、top、bottom分别代表螺旋管近轴侧、远轴侧、上侧及下侧的四条母线。

本文采用ICEM软件对模型进行网格划分，划分方式采用O型切分。为保证计算精度，在近壁面采用增强壁面处理方法，将各工况的y+（无量纲壁面距离）定为1左右。对划分好的网格进行网格无关性验证后，选定网格节点数为175万的网格为计算所用网格。

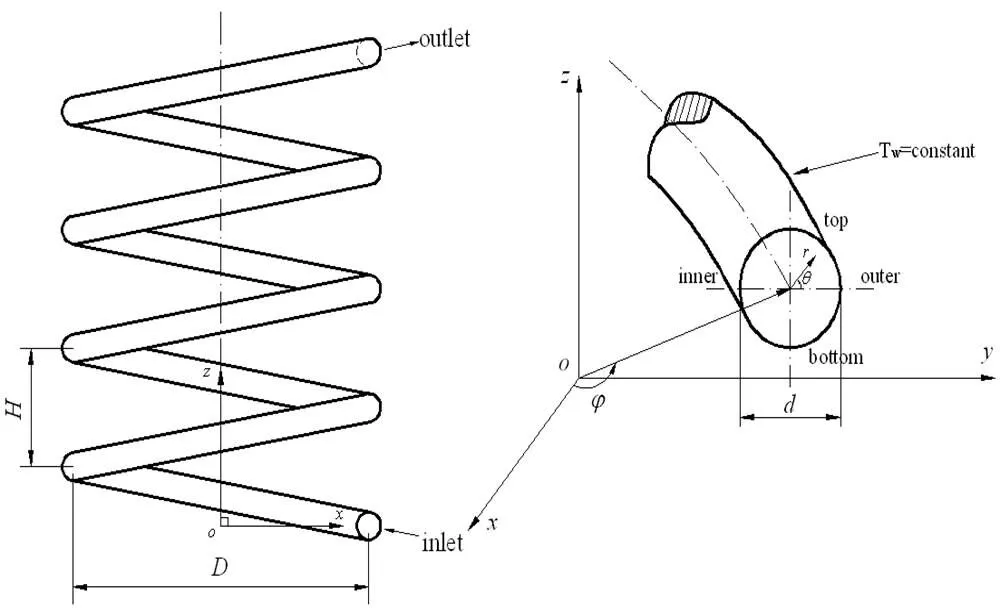
图1 螺旋管几何模型示意图

本文采用FLUENT软件对模型进行求解。入口设为质量进口条件，出口设为压力出口条件，壁面设为无滑移的壁面条件，采用等壁温加热的方式。CO2在不同温度和压力下的物性参数在REFPROP软件中获取，并在FLUENT求解器中按piecewise-liner方法将相关参数逐个输入。在求解器的设置方面，压力-速度耦合采用SIMPLEC算法，Skewness Correction设为1，动量、能量、湍动能以及湍动能耗散率的离散格式均选用QUICK格式。

1.2 数学模型

连续性方程为：

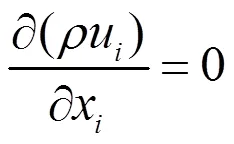
动量方程为：

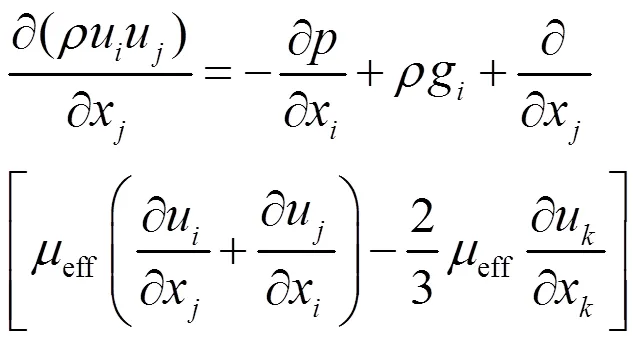
能量方程为：

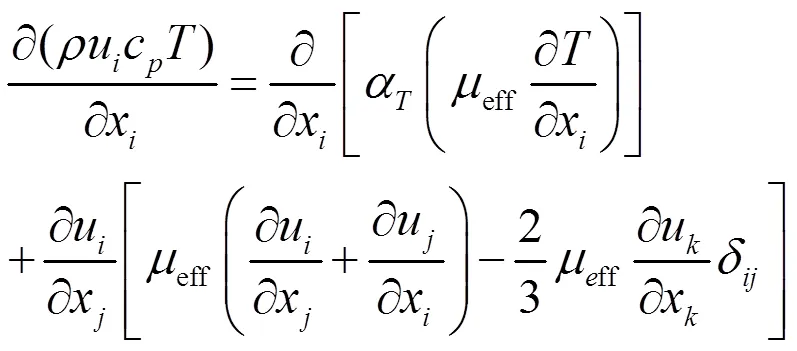
式中：eff为湍流有效粘度。

对于湍流模型，本文选用在计算旋转流方面有较高精度的RNG-两方程模型[15]：

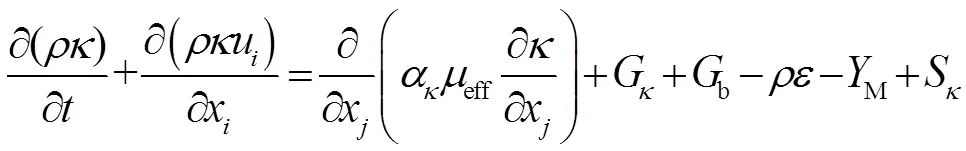
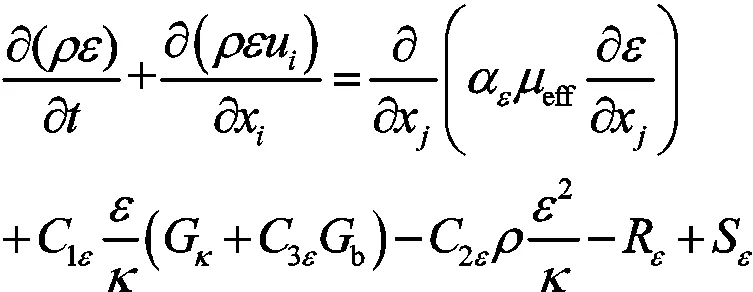
式中：G表示由层流速度梯度而产生的湍动能项，b表示由浮力产生的湍动能项，M表示在可压缩流动中，湍流脉动膨胀到全局流程中对耗散率的贡献项，1、2、3为经验常数，α和α分别为方程和方程的湍流数，S和S是湍动能和湍流耗散源项。

主流平均温度b为：

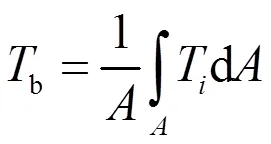
式中：为管道横截面积。

壁面局部传热系数为：

（7）

式中：为热通量；w为壁面温度。

2 模拟结果及分析

2.1 计算模型验证

为验证模型的正确性，对Zhang等[13]的实验工况进行模拟。在该工况下，压力=8.02MPa，单位面积质量流量s=97.92kg/m2·s，入口温度0=288.15K，热通量=10.4kW/m2。实验中所用螺旋管尺寸与本文所建模型相同。图2为模拟的不同截面处主流平均温度随/的变化与Zhang等的实验数据的对比。图中的横坐标表示该截面至入口截面的距离与管径的比值。如图2所示，模拟所得的结果与实验数据基本吻合，误差很小，说明本文所用模型能够较好地模拟超临界CO2在螺旋管内的对流换热过程。

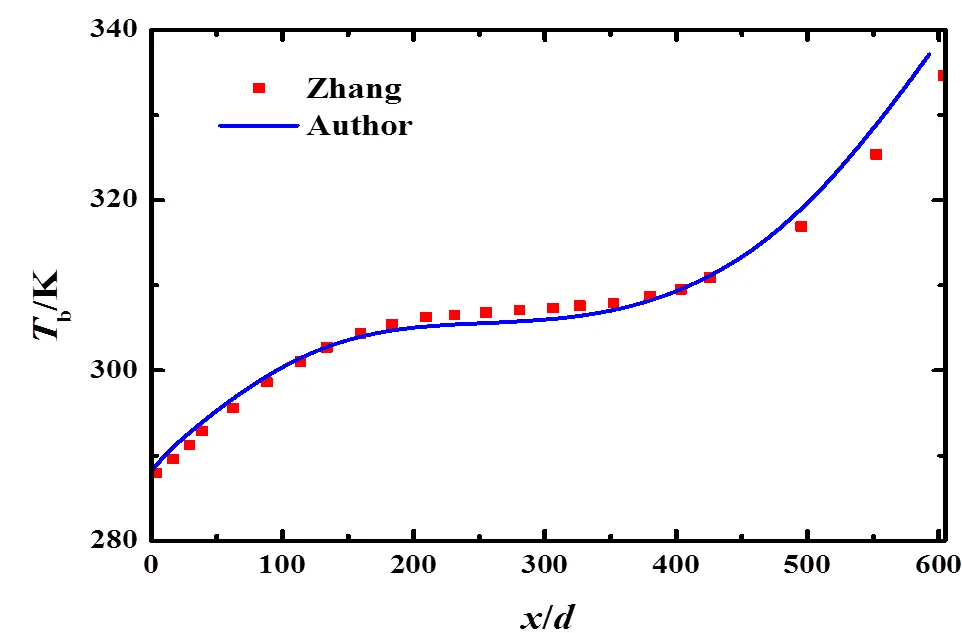
图2 本文模拟主流平均温度Tb随x/d的变化情况与 文献[13]对比

2.2 温度、密度及流速

本模拟工况的相关条件设定为：压力=7.6MPa，质量流量0=0.0352kg/s，入口温度0=288.15K，壁面温度w=323.15K，重力加速度=9.807m/s2。图3给出了螺旋管不同轴向角处的截面温度、密度及流速分布状况。为统一视角，图中各截面均以左侧作为螺旋管靠近轴线的一侧（近轴侧），右侧作为远离轴线的一侧（远轴侧）。

=180°处的截面呈现的是流体刚被管壁加热不久时的状态。从图中可以看出，=180°的截面温度、密度及流速分布的对称轴呈倾斜状态。这是流体受到浮升力和离心力的共同作用所致。一方面，当流体刚被加热时，近壁面流体开始进入拟临界区，密度迅速变小，从而与主流流体形成密度差产生浮升力的作用，使高温低密度流体流向上部，低温高密度流体流向下部。另一方面，流体在螺旋管内作曲线运动，低温高密度流体在流动过程中受离心力的影响比高温低密度流体大，使得这部分流体向远离轴线一侧的管壁靠近，以便能够借助外侧管壁提供的足够大的向心加速度来支持其作曲线运动，而高温低密度流体受离心力影响较小，会在远轴侧的低温高密度流体挤压下流向靠近轴线的一侧。正是由于以上两方面的因素导致低温高密度流体聚集在了管远轴侧下部区域，而高温低密度流体聚集在了管近轴侧上部区域。

CO2在7.6MPa压力下的拟临界温度为305.45K。如图3（a）所示，在=360°处，位于管近轴侧上部的部分流体的温度已处于拟临界温度附近。当超临界流体的温度处于拟临界温度附近时，很小的温度差便会导致很大的密度变化，使得图3（b）中=360°处密度云图出现了较多的分层。该现象同样能够在图3（b）中=720°、900°处被观察到。在=720°处，管内流体已全部处于拟临界温度。由于在拟临界区CO2的比热较之前会大增，使得流体温升变得很慢，管内温度在很长一段距离范围内均保持在拟临界温度附近，没有进一步升温的迹象。因此，在=900°处，流体的温度与=720°处的温度相比并没有改变，依然维持在拟临界温度上下。对比图3（b）中=720°、900°处的密度云图则可以发现，后者的密度较前者明显变小，这反映流体在拟临界区物性参数发生了剧烈的变化，密度出现了陡降。

=1350°、1980°处的截面显示的是流体离开拟临界区之后的状态。从图3（a）中可以看出，流体经过一段距离的加热后逐渐远离了拟临界区，开始进一步升温。观察图3（b）中=1350°处的密度分布可以发现，虽然此时管内仍有温度差，但密度分层已不太明显，在=1980°处，管内密度已呈均匀分布。这说明流体经过拟临界区后，密度已不再随温度的升高而发生明显的改变。

随着流体温度的升高，流体的流速也逐渐增大，从图3（c）中可以看出，在=1350°处出现了明显的流速分层。对于流体在直管内的流动而言，其截面流速一般呈同心圆分布，流体在螺旋管内流动所形成的截面流速分布则与之不同。因为流体在螺旋管中流动会受到离心力的影响，在远轴侧除层流底层之外的流体流速会大于近轴侧流体的流速，故其截面上的流速呈图3（c）所示的分布。

观察图3中螺旋管各截面对称轴的变化可以发现，当≤900°时，各截面的温度、密度、速度分布云图的对称轴均呈倾斜状态，说明在该区间，流体在流动传热过程会受浮升力和离心力的共同影响，浮升力的影响在流体离开拟临界区之前不能忽略。当≥1350°之后，螺旋管截面的温度、密度及流速已呈上下对称分布，表明流体已经离开了拟临界区，浮升力的影响可以被忽略，流体的温度、速度及密度分布受离心力作用的支配。

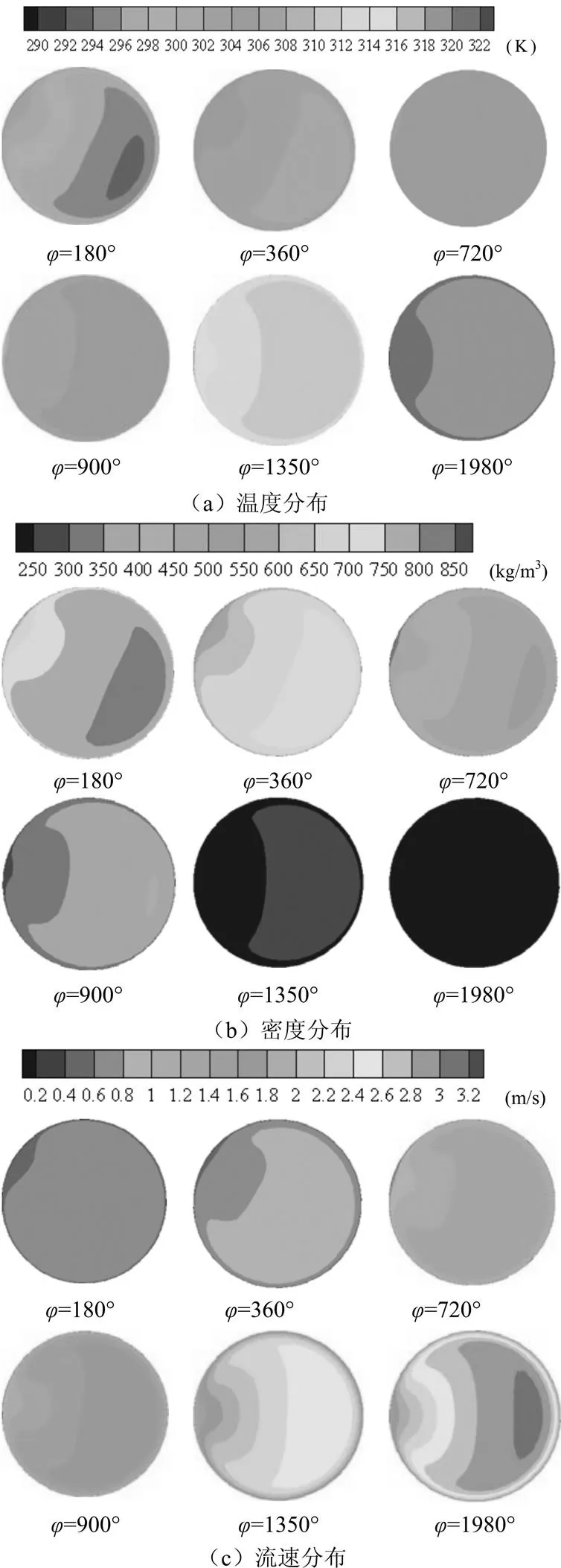
图3 不同截面处温度、密度、流速云图（左侧为近轴侧）

2.3 对流传热系数

图4给出了超临界CO2在螺旋管内等壁温加热条件下，top、bottom、outer和inner四条母线上局部对流传热系数沿轴向角的变化情况。从图中可以看出，四条母线上的对流传热系数均呈现在入口处先减小，不久之后开始增大，到达峰值后又逐渐减小的变化规律。各母线在入口处最大，是因为入口附近温度边界层还未形成，流体与壁面间的对流换热非常充分。在这之后急剧下降则是由于边界层开始形成并增厚所造成的。随着流体在螺旋管内被加热，进入拟临界区，各物性参数开始发生剧烈变化，物性参数的剧烈改变使得对流传热系数开始增大。在=540°处，inner母线的首先到达峰值，其余三条母线的对流传热系数在=720°附近位置处也达到了峰值。图3中=720°处的截面反映了流体top、bottom、outer三条母线的对流传热系数处于峰值时管截面的温度、密度及流速分布情况。可以发现，当三条母线的达到峰值时，流体主流温度刚好处于305.45K的拟临界温度上下，这说明流体在拟临界区物性参数的剧烈变化增强了流体与管壁间的换热，是使对流传热系数增大的直接原因。inner母线的先于其他三条母线到达峰值是因为在离心力所引发的二次流作用下，inner母线附近聚集了温度较主流流体温度更高的流体，这部分流体由于温度更高，更早到达拟临界区发生物性参数的改变，因此inner母线上的最先达到峰值。

对比四条母线还可以发现，当≤1035°时，bottom母线上的最大，inner母线上的最小。不同母线上值的差异与不同壁面位置处的二次流强弱有关。当<1350°时，流体在流动过程中受到浮升力与离心力的共同影响，使管壁不同位置处出现强度不等的二次流。inner母线位于螺旋管内侧壁面，其附近的流体在离心力的影响下呈现远离壁面的运动趋势，使得该处的二次流强度最弱，bottom母线上的较大则是因为在浮升力引发的二次流影响下，螺旋管下部的高密度流体受上部低密度流体压迫冲刷下部壁面，使bottom母线附近的二次流强度强过了上部区域的二次流。正是由于二次流在管内不同位置处强弱不一使得四条母线上的值的大小存在差距。

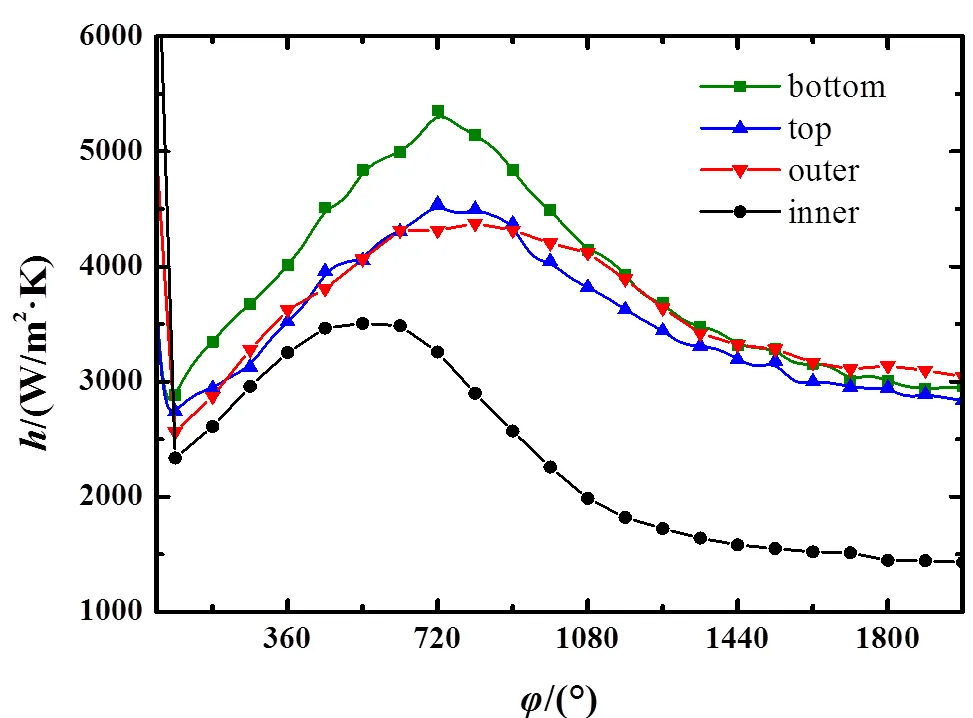
图4 四条母线上的h随φ的变化

为探究壁面温度的变化对传热过程的影响，图5给出了壁面温度分别为323.15K、338.15K和353.15K时上侧母线局部对流传热系数沿轴向角的变化情况。如图5所示，壁面温度的增大会使拟临界区内的峰值有所减小。这说明壁面温度的变化会影响流体各热物性参数随温度的变化，从而间接改变了的大小。另外，随着壁面温度的增大，流体在拟临界区出现峰值时对应的轴向角会减小。这是由于壁面温度越高，在入口温度相同的情况下流体与壁面间的温差就越大，流体升温也就更快，因而使流体更早地进入拟临界区。

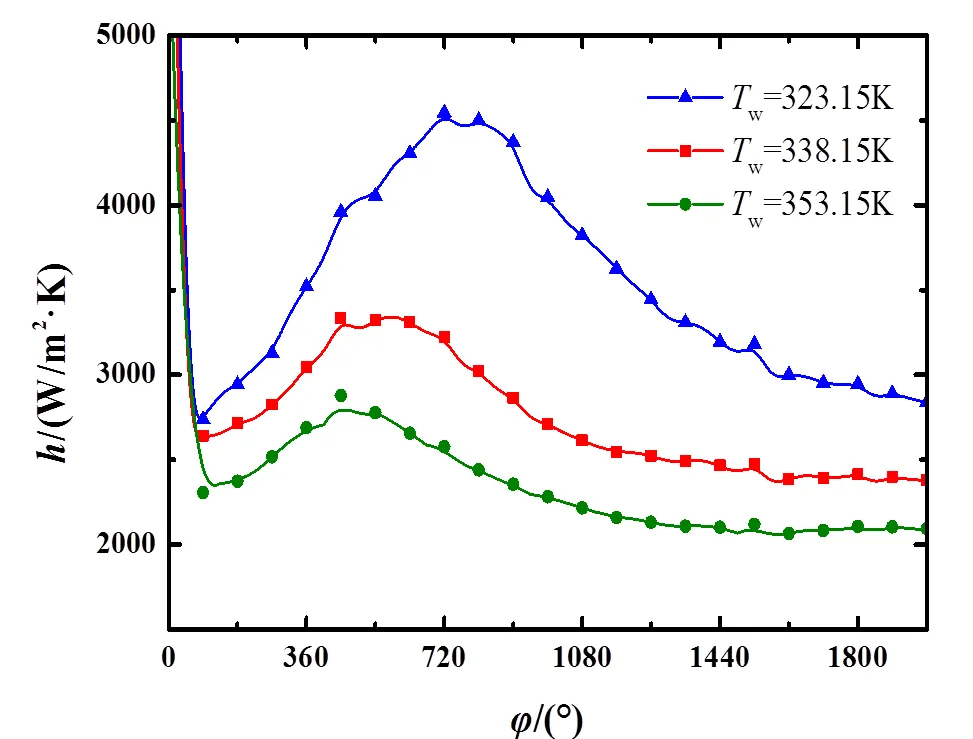
图5 不同Tw下局部h随φ的变化

3 结论

通过对等壁温条件下超临界CO2在螺旋管内的对流传热过程进行数值模拟，可得出以下结论：

（1）超临界CO2在螺旋管内的流动与传热会受到离心力与浮升力的影响，离心力的影响在整个流动过程中均存在，浮升力的影响在流体离开拟临界区之前不能忽略；

（2）局部对流传热系数在入口处先减小，不久后增大，到达峰值后又逐渐减小。在浮升力与离心力的影响下，螺旋管不同壁面位置处的局部对流传热系数的大小有所不同；

（3）局部对流传热系数的峰值会随壁面温度的增大而减小，峰值出现的位置则会随壁面温度的变大向入口方向移动。

4 致谢

感谢台北科技大学颜维谋教授在课题研究及论文写作过程中所提供的帮助。

[1] Bruch A, Bontemps A, Colasson S. Experimental investigation of heat transfer of supercritical carbon dioxide flowing in a cooled vertical tube[J]. International Journal of Heat and Mass Transfer, 2009,52(11-12): 2589-2598.

[2] Tanimizu K, Sadr R. Experimental investigation of buoyancy effects on convection heat transfer of supercritical CO2flow in a horizontal tube[J]. Heat and Mass Transfer, 2016,52(4):713-726.

[3] 徐轶君,姜培学,石润富,等.超临界CO2在微细圆管中对流换热实验研究[C].第六届全国低温与制冷工程大会会议论文集,2003.

[4] 徐轶君,姜培学,向恒,等.竖直细圆管中超临界CO2对流换热实验研究[J].工程热物理学报,2004,25(S1):87-90.

[5] 徐轶君,姜培学,张宇,等.竖直圆管中超临界压力CO2在低雷诺数下对流换热研究[J].工程热物理学报,2005, 26(3):468-470.

[6] 饶政华,廖胜明.超临界二氧化碳管内湍流流动和传热的数值模拟[J].流体机械,2005,33(1):71-75.

[7] 饶政华,廖胜明.超临界CO2水平细微管内层流流动与换热的数值模拟[J].热科学与技术,2005,4(2):113-117.

[8] 饶政华,廖胜明.二氧化碳微通道气体冷却器的数值仿真与性能优化[J].化工学报,2005,56(9):1721-1726.

[9] 饶政华,廖胜明.超临界CO2在水平三角细微管内层流对流换热的数值模拟[J].制冷学报,2006,27(5):43-47.

[10] 杨传勇,徐进良,王晓东,等.超临界参数CO2在倾斜管内对流换热数值模拟[J].热力发电,2013,42(1):26-35.

[11] 杨传勇,徐进良,王晓东,等.管道倾斜角度对超临界CO2管内换热特性的影响[J].原子能科学技术,2013,47(9): 1522-1528.

[12] 齐伟,毛宇飞,刘庆君.冷却管内超临界二氧化碳对流传热Matlab分析[J].制冷与空调,2015,29(3):341-344.

[13] Zhang W, Wang S, Li C, et al. Mixed convective heat transfer of CO2at supercritical pressures flowing upward through a vertical helically coiled tube[J]. Applied Thermal Engineering, 2015,88:61-70.

[14] 李洪瑞,徐肖肖,刘朝,等.螺旋管内超临界CO2流动方向对换热的影响[J].航空学报,2016,37(7):2123-2131.

[15] Yakhot V, Orszag S A. Renormalization group analysis of turbulence. I. Basic theory[J]. Journal of Scientific Computing, 1986,1(1):3-51.

Numerical Simulation of Convective Heat Transfer of Supercritical CO2in a Helical Tube under Constant Wall Temperature Condition

Gu Qian Yu Nanyang

( School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, 610031 )

The convective heat transfer of supercritical CO2in a helical tube under constant wall temperature condition was numerically simulated.The distribution of temperature, velocity and density in the convective heat transfer to the supercritical CO2in the helical tube were obtained and analyzed. The variation law of the local convection heat transfer coefficient of the supercritical CO2along the axial angle in the helical tube was summarized. The impacts of changing wall temperature on the local convective heat transfer coefficient of helical tube were discussed. The results show that the influence of centrifugal force is existing in the whole convective heat transfer process, and the influence of buoyancy can not be neglected before the fluid leaves the pseudocritical region; when the axial angle≤1035°, the convective heat transfer coefficient at the bottom generatrix is the largest, the convection heat transfer coefficient at the inner generatrix is the smallest and increase to the peak value first; the peak value of the local convective heat transfer coefficient decreases with the increase of the wall temperature.

constant wall temperature; helical tube; supercritical CO2; convective heat transfer; numerical simulation

1671-6612（2017）06-576-06

TK124

A

顾 骞（1991-），男，在读硕士研究生，E-mail：mike9300@126.com

余南阳（1961-），男，博士，教授，博士生导师，E-mail：rhinos@126.com

2017-04-17