聚酯/聚酰胺中空橘瓣型超细纤维非织造材料的孔径预测
2018-01-29钱晓明杨红英申屠宝卿张一风刘让同
张 恒, 甄 琪, 钱晓明, 杨红英, 申屠宝卿, 张一风, 刘让同
(1. 中原工学院, 河南 郑州 451191; 2. 武汉纺织大学 纺织纤维及制品教育部重点实验室, 湖北 武汉 430070;3. 浙江大学 化学工程与生物工程学院, 浙江 杭州 310027; 4. 天津工业大学 纺织学院, 天津 300387)
超细纤维非织造材料作为由超细纤维相互连接而成的网状多孔柔性材料,在渗透、过滤与分离等领域具有广泛的应用。其应用在很大程度上依赖于纤维间的孔隙对细小颗粒物和对连续流体自由流动的拦截作用[1],因此,分析非织造材料的孔径分布对于研究非织造材料的过滤和渗透机制是有益的。
作为一种新型超细纤维非织造材料,基于水刺原纤化的双组分纺粘超细材料与静电纺丝、熔喷等超细纤维非织造材料相比,不仅具有比表面积大、柔软舒适的特点,还具有安全、环保、强力高等特点,在擦拭布、皮革基布和过滤领域具有广泛应用[2-3]。现有研究多围绕开纤机制[4]、材料的功能性应用[5]等方面进行分析,这为使用数学方法描述其结构特征提供了基础。LU等[6]探究了聚酯(PET)/聚酰胺(PA6)橘瓣型双组分纺粘非织造材料的水刺开纤工艺与形态结构的物理关系,并证明利用实验方法获得开纤率是可行的;Hollowell等[7]则进一步明确了样品的模态孔径受材料厚度和双组分纤维开裂程度的影响。
目前关于非织造材料孔隙分布的研究以实验测试方法为主,采用数学模型预测的方法相对较少。Faure等[8]假设纤维在材料表面的排列是各向同性的,并将纤维看作是随机排列的直线,将材料的孔径看作是能通过直线间隙的圆,同时认为圆的直径的概率分布符合泊松分布,建立了纤维特性和材料的结构特性与孔径分布的数学关系。此后,人们在Faure研究的基础上不断地进行完善并应用:Lombard等[9]修正了数学关系中材料的结构特性对孔径分布的影响;Rawel等[10]则对材料中纤维排列角度对孔径分布的影响进行了修正。文献[11-13]在这个模型的基础上对非织造材料的孔径分布进行了数学分析和预测,但是现有研究没有表明,是否存在一种有效的数学模型可以预测同时含有开裂超细纤维和未开裂双组分纤维的PET/PA6中空橘瓣型超细纤维非织造材料的孔径[14]。
本文在前人研究的基础上,通过对PET/PA6中空橘瓣型超细纤维非织造材料的纤维几何形态和结构特征进行分析,引入概率平均直径以构建双组分超细纤维非织造材料的孔径模型。对PET/PA6中空橘瓣型超细纤维非织造材料的孔径研究可以为PET/PA6橘瓣型双组分纺粘水刺非织造材料在土工、过滤等领域的应用提供基础。
1 实验部分
1.1 样品的制备
将热塑性聚合物切片(PET切片和PA6切片)分别经螺杆挤出机软化、熔融后送入计量泵中,定量挤出的聚合物熔体经过双组分纺丝模头挤出成型,此后经冷却风、牵伸气流的冷却、牵伸作用在成网帘上铺放成均匀的双组分纤维网,然后双组分纤维在高压水射流的冲击作用下开裂成超细纤维并相互缠结成型。
聚合物切片为聚对苯二甲酸乙二醇酯(PET)切片(仪征化纤有限责任公司)、聚酰胺6(PA6)切片(无锡龙诚化纤有限公司),所用切片的参数如表1所示。

表1 聚合物切片参数Tab.1 Basic properties of polymers
注:Mw为重均相对分子质量;Mn为数均相对分子质量。
PET/PA6中空橘瓣型纤维截面如图1所示。纤维由8份PET和8份PA6交替排列而成,PET和PA6的体积比为7∶3。纤维细度为(17.8±1.2)μm,纤维的空心圆直径为(4.2±0.8)μm。

图1 PET/PA6中空橘瓣型双组分纤维截面Fig.1 Cross section of PET/PA6 hollow segmented-pie bicomponent fibers
现有文献已表明双组分纤维开裂的主因是水射流冲击作用,单位时间内单位质量的纤维网所承受的水针冲击总能量Es表示为
(1)
式中:Es为单位体积纤维网所受的水针冲击能量,kJ/m3;cv为孔口流速系数,0.98;cq为孔口流量系数,0.98;ρ为水的密度,998 kg/m3;w为纤网面密度,g/m2;v为纤网前进速度,m/s;di为第i个水刺头的水针孔径,120 μm;pi为水针压力,Pa;Ni为水针孔密度,1 667孔/m。
1.2 样品的结构特征参数测试
对PET/PA6中空橘瓣型超细纤维非织造材料的结构特征参数和孔径分布进行研究。通过TM1000型台式扫描电子显微镜(日本株式会社日立制作所)分析材料的结构和纤维的截面形态,采用PSM-165型孔径测试仪(Topas®)测试材料的孔径分布。采用YG141LA型数字式织物厚度仪测定材料的厚度,压脚面积为1 000 mm2,压脚重力为500 cN。材料的孔隙率由式(2)计算得出。试样的特征参数如表2所示。
(2)
式中:P为材料的孔隙率,%;u为面密度, g/m2;Th为厚度,mm;ρf为纤维的平均密度,kg/m3。
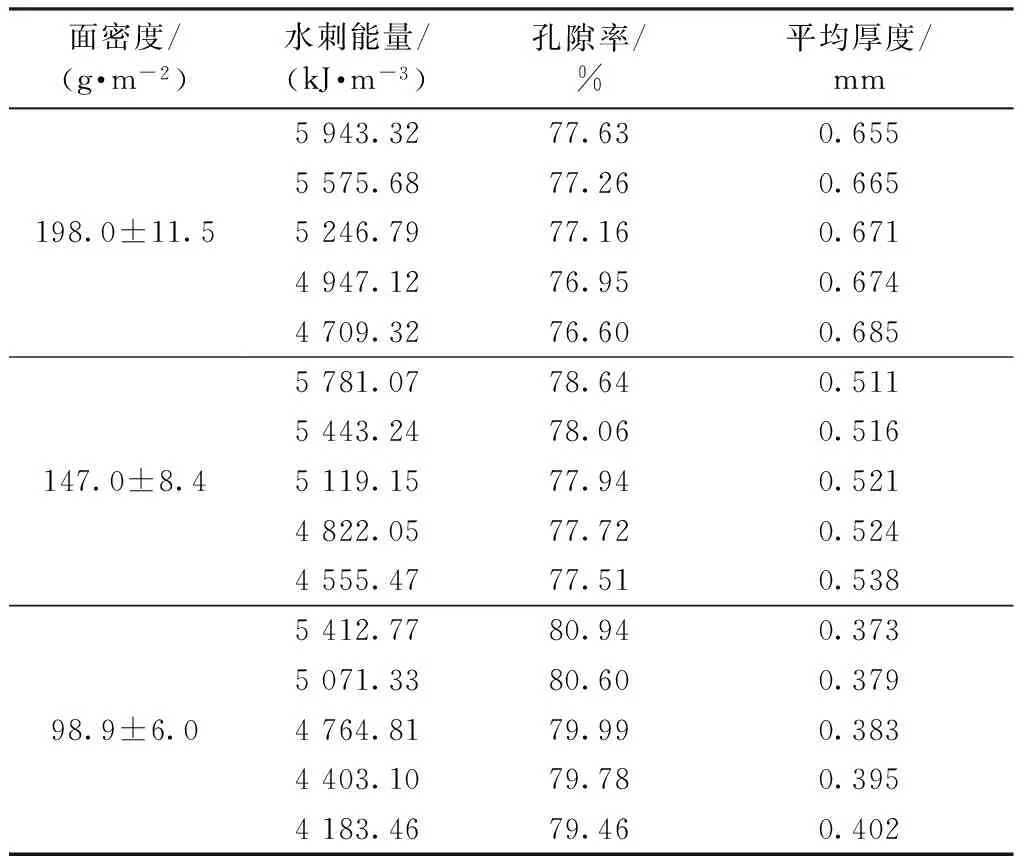
表2 材料的特征参数Tab.2 Characteristic parameters of samples
2 孔径模型的构建
2.1 双组分非织造材料形态特征
图2示出样品的表面和横截面扫描电镜照片。可以看出:双组分纤维在高压水射流的作用下开裂成超细纤维并相互纠缠形成致密的网状结构;同时,开裂后纤维相互缠结成纤维束,并在样品表面进行杂乱无序的排列,进而相互交叉在材料表面形成较大的孔洞。结合样品的横截面扫描电镜照片可看出,这些孔洞并没有贯穿整个材料,因此,可认为材料厚度方向上的孔隙大小取决于材料内部纤维间缝隙大小。从图2还可看出,纤维主要在水平方向上分布,而在厚度方向上排列较少。这可能是由于双组分纺粘的气流成网方式导致的,在双组分纺粘成型过程中,纤维在气流分丝的作用下一层层铺放而成。此外,从图2还可得到单位面积(l×h)内未开裂的双组分纤维的数目,这为通过试样横截面电镜照片获得开纤率提供了可能性。
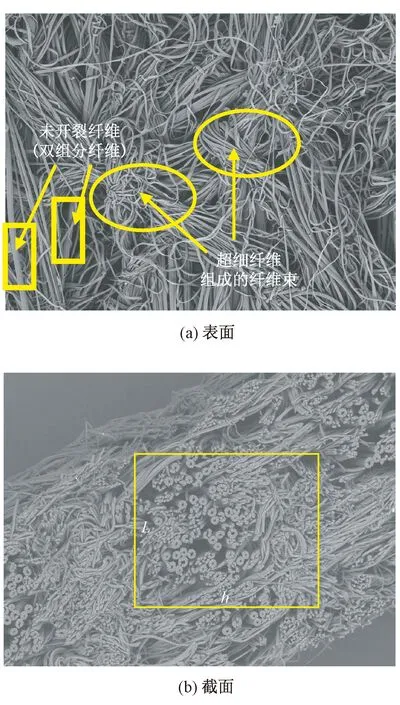
图2 样品的扫描电镜照片(×200)Fig.2 SEM images of samples(×200). (a) Surface; (b) Cross sections
开纤率是表征双组分纤维开纤程度的指标[14]。通过对材料的横截面扫描电镜照片进行分析,利用式(3)得出开纤率
(3)
式中:Sr为开纤率,%;N为单位面积中未开裂纤维的根数;N0为单位面积中所有未开纤前纤维的根数。
N0=l×h×P/sf
式中:l为样品长度,mm;h为样品宽度,mm;sf为双组分纤维截面面积,μm2。
2.2 基于概率平均直径的孔径模型构建
2.2.1Faure孔径模型
平均随机分割是指假设有一平面被随机直线网分割,则平面被直线网分割成无数多边形。根据Poisson-Polyhedron理论,这些多边形的最大内接圆直径大于或等于d的频率[8]为
(4)
(5)
式中:d为孔径,m;ω为特征长度,m-1。
若将这些多边形等效为多孔介质的圆形孔隙,则G(d)即为孔隙中孔径大于或等于d的累积概率。孔径小于d的累积概率[8]为
F(d)=1-G(d)
(6)
PET/PA6中空橘瓣型超细纤维非织造材料可以看作是由多层薄型纤网逐层排列而成,每层纤网均由纤维和纤维间的孔隙组成,且每层薄型纤维网之间相互独立。假设纤维只在水平方向呈直线随机平面交叉分布,同时假设纤维的界面全部为圆形,根据上述分析,依据现有孔径预测模型公式可获得双组分非织造材料的孔径累积频率
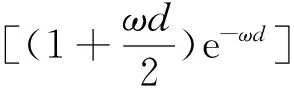
(7)
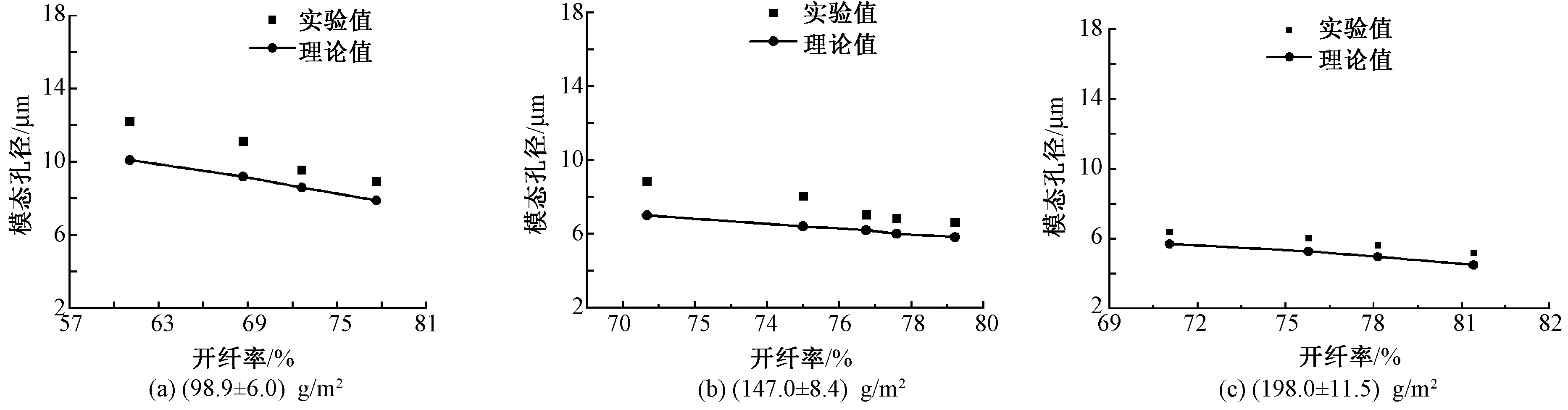
图3 不同面密度样品的模态孔径随开纤率的变化Fig.3 Mean pore size vs. splitting rate for samples
式中,N为组成双组分非织造材料的薄型纤维网层数。Faure等[8]假定薄型纤维网厚度为纤维直径;Lombard等[9]假定薄型纤维网厚度为2倍的纤维直径;Rawal等[15]假定薄型纤维网厚度为概率平均直径。
2.2.2概率平均直径的引入
基于双组分超细纤维的特点,假定薄型纤维网厚度为概率平均直径的2倍,即
(8)
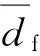
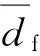
(9)
式中:dpet为PET超细纤维直径,μm;dpa6为PA6超细纤维直径,μm;df为双组分纤维直径,μm;φpet为PET超细纤维体积分数,%,φpet=0.7sr;φpa6为PA6超细纤维体积分数,%,φpa6=0.3sr;φf为双组分纤维体积分数,%,φf=1-sr。
根据式(4)~(9)建立PET/PA6中空橘瓣型超细纤维非织造材料的孔径预测模型
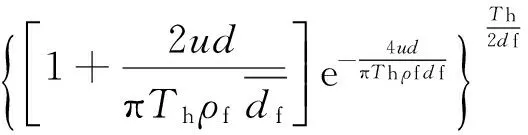
(10)
3 结果与讨论
3.1 模型验证
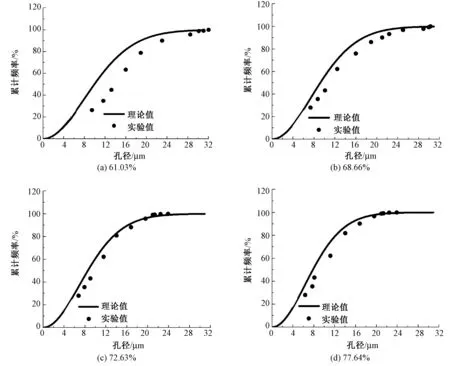
图4 不同开纤率样品孔径累计频率理论值和实验值对比曲线Fig.4 Comparison between theoretical and experimental pore size distributions of samples
为验证PET/PA6中空橘瓣型超细纤维非织造材料孔径预测模型的可预测性,对不同开纤率试样的孔径分布进行对比和分析。图3示出不同面密度试样的模态孔径随开纤率变化的理论值和实验值的对比曲线。图4示出面密度为(98.9±6.0)g/m2材料的孔径累积频率理论值和实验值对比曲线。
从图3可看出,开纤率和面密度对孔径有显著的影响,且理论预测值与实测值吻合度较高,均表现为孔径随着开纤率的增大而减小。这是由于随着开纤率的增大,单位体积内超细纤维的数量增多,从而纤维间的孔隙减小导致结构致密;此外,材料厚度的增大使得厚度方向上的纤维叠加概率增大,进而纤维间孔隙的堵塞概率增大,引起孔隙在厚度方向的弯曲和不连续。此变化趋势与现有研究结果相符。
实验值和理论值存在误差的原因为:1)纤维并不是全部在水平方向上杂乱排列,超细纤维在样品表面形成的纤维束也会对孔径分布造成影响,只是限于现有技术条件无法定量分析其影响规律。2)纤维材料的结构和纤维排列并不是各向同性的,从图2可看到在材料表面的水射流的痕迹(规则的较大孔隙),这些孔洞的尺寸和分布受水刺工艺的影响,同时会对孔径大小造成影响。3)模型的建立和运算是基于纤维为规则的圆形截面,而超细纤维的细度和纤维界面并不规整,这也会对孔径分布造成影响。4)双组分纤维的开纤率对材料的孔径分布有很大的影响,开纤的实际情况和纤维开裂程度对非织造材料的孔径有一定的影响。5)测试误差。
3.2 孔径分布的预测分析
现有的大量实验研究结果表明,影响非织造材料孔径大小的主要因素是纤维的特征和加工方式。对于PET/PA6中空橘瓣型超细纤维非织造材料来说,影响其孔径大小的主要因素是纤维细度、开纤率等结构参数[3]。利用所构建的PET/PA6中空橘瓣型超细纤维非织造材料的孔径预测模型分析纤维的细度和开纤率对孔径大小的影响,具有非常现实的指导意义。图5示出孔径分布和开纤率的理论关系曲线。可以看出,随着开纤率的增大,孔径呈现减小的趋势。
图6示出孔径大小与纤维细度的关系。可以看出,随着纤维直径的减小,材料的孔径分布同样呈现减小的趋势,这与前人的研究结果[2]相符。
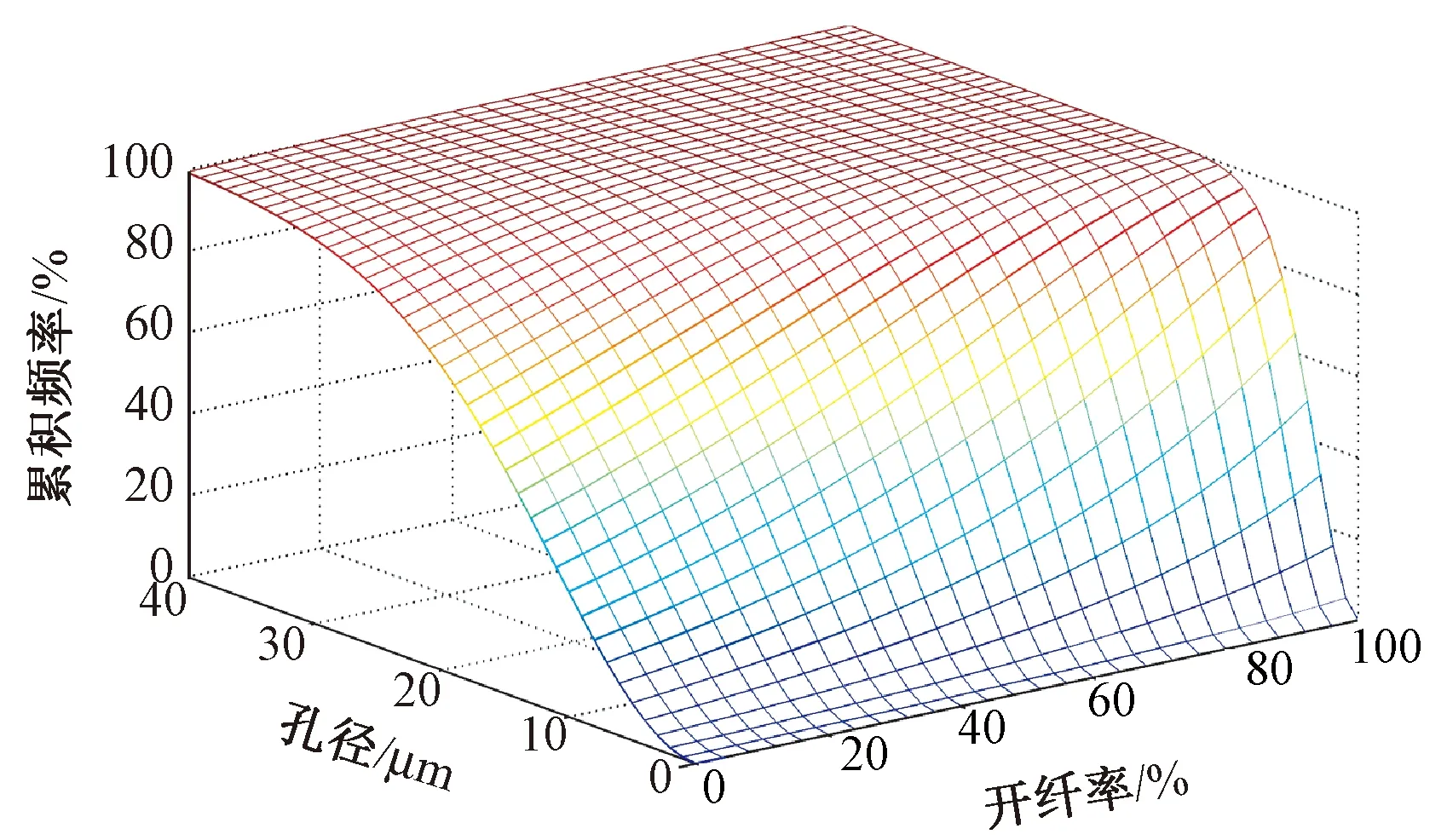
图5 孔径分布和开纤率的理论关系曲线(Th=0.465 mm,df=17.8 μm)Fig.5 Theoretical curve of pore size distribution vs. splitting rate(Th=0.465 mm,df=17.8 μm)
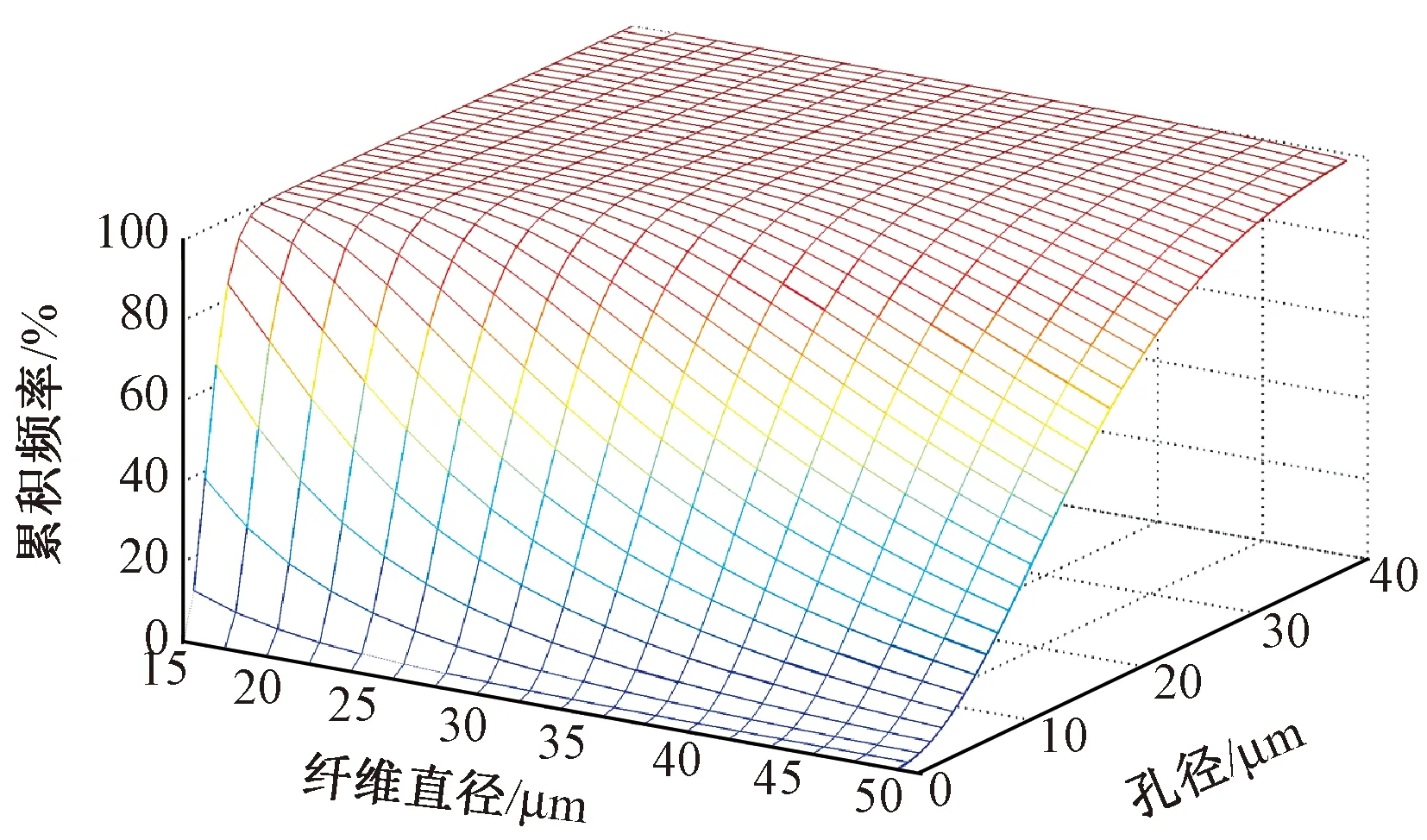
图6 孔径分布和纤维细度的理论关系曲线(Th=0.465 mm,Sr=80%)Fig.6 Theoretical curve of pore size distribution vs. fiber diameter(Th=0.465 mm,Sr=80%)
4 结 论
在对基于水刺原纤化PET/PA6中空橘瓣型超细纤维非织造材料结构特征研究的基础上,尝试对Faure孔径模型引入概率平均直径以表征其孔径特征。
1)验证结果表明,基于概率平均直径的孔径预测模型所得的理论曲线和实验所得数值重合性较好,且随着材料面密度(厚度)的增加,重合性逐渐提高。
2)利用所建立的模型对材料的开纤率和纤维细度与材料孔径的关系进行模拟分析,获得了PET/PA6中空橘瓣型双组分超细纤维非织造材料的孔径特征随开纤率、厚度、纤维细度等结构参数变化而变化的规律。
通过以上研究,不仅可获得PET/PA6中空橘瓣型双组分超细纤维非织造材料的孔径预测模型,还可将孔径特征与开纤率、厚度、纤维细度等结构参数的模拟研究用于PET/PA6中空橘瓣型双组分超细纤维非织造材料的的参数化建模,从而为进一步拓展PET/PA6橘瓣型双组分纺粘水刺非织造材料在土工、过滤等领域的应用提供参考。
[1] 王成, 姚理荣, 陈宇岳. 芳纶纳米纤维毡/聚苯硫醚高温超过滤材料的制备及其性能[J]. 纺织学报, 2013, 34(7): 1-4.
WANG Cheng,YAO Lirong,CHEN Yuyue. Preparation and properties of high temperature resistant ultrafiltration aramid nanofiber/PPS composite material[J]. Journal of Textile Research, 2013, 34(7): 1-4.
[2] HENG Z, QIAN Xiaoming, ZHEN Qi, et al. Research on structure characteristics and filtration performances of PET-PA6 hollow segmented-pie bicomponent spunbond nonwovens fibrillated by hydro entangle method[J]. Journal of Industrial Textiles, 2015, 45(1):48-65.
[3] 张恒, 钱晓明, 宋卫民,等. 双组分纺黏水刺非织造材料的过滤性能[J]. 东华大学学报(自然科学版), 2014, 40(2):171-175.
ZHANG Heng, QIAN Xiaoming, SONG Weimin, et al. Filtration performance of the bicomponent spunbonded nonwoven material based on the hydroentanglement[J]. Journal of Donghua University (Natural Science Edition), 2014, 40 (2): 171-175.
[4] SUVARI F, ULCAY Y, MAZE B, et al. Acoustical absorptive properties of spunbonded nonwovens made from islands-in-the-sea bicomponent filaments[J]. Journal of the Textile Institute, 2013, 104(4): 438-445.
[5] YEOM B Y, POURDEYHIMI B. Aerosol filtration properties of PA6/PE islands-in-the-sea bicomponent spunbond web fibrillated by high-pressure water jets[J]. Journal of Materials Science, 2011, 46(17): 5761-5767.
[6] LU Z M, QIAN Xiaoming. Combination technology of spunbond & spunlace[J]. Advanced Materials Research, 2011, 331: 241-244.
[7] HOLLOWELL K B, ANANTHARAMAIAH N, POURDEYHIMI B. Hybrid mixed media nonwovens composed of macrofibers and microfibers: part I: three-layer segmented pie configuration[J]. Journal of the Textile Institute, 2013,104(9): 1-8.
[8] FAURE Y H, GOURC J P, GENDRIN P. Structural study of porometry and filtration opening size of geotextiles [J]. Geosynthetics: Microstructure and Performance, 1990, 1076: 102-119.
[9] LOMBARD G, ROLLIN A, WOLFF C. Theoretical and experimental opening sizes of heat-bonded geotextiles[J]. Textile Research Journal, 1989, 59(4): 208-217.
[10] RAWAL A, KAMESWARA Rao P V, RUSSELL S, et al. Effect of fiber orientation on pore size characteristics of nonwoven structures[J]. Journal of Applied Polymer Science, 2010, 118(5): 2668-2673.
[11] 吴兆平, 李艰. 非织造土工布几何结构与孔径分布计算[J]. 上海工程技术大学学报, 1997, 11(3): 23-27.
WU Zhaoping, LI Jian. Calculation of nonwoven geotextile geometric structure and pore size distribution[J]. Journal of Shanghai University of Engineering Science, 1997, 11(3): 23-27.
[12] 刘丽芳, 王卫章, 储才元, 等. 非织造土工布孔径分布与渗透性能关系的研究[J]. 产业用纺织品, 2003, 21(3): 17-20.
LIU Lifang, WANG Weizhang, CHU Caiyuan. Study on relation between pore size distribution and permeability of nonwoven geotextile[J]. Technical Textiles, 2003, 21(3): 17-20.
[13] 田正宏, 刘兆磊, 张丹, 等. 透水模板布孔径分布测试方法与理论研究[J]. 建筑材料学报, 2009, 12(6): 639-642.
TIAN Zhenghong, LIU Zhaolei, ZHANG Dan, et.al Measurement of pore size distribution of controlled permeabil ity formwork liner[J]. Journal of Building Materials, 2009, 12(6): 639-642.
[14] 钱小刚,吴中元,张恒. 双组分纺粘非织造过滤材料的结构设计[J]. 天津纺织科技,2015(1):16-18.
QIAN Xiaogang, WU Zhongyuan, ZHANG Heng. Structural design of bicomponent spunbonded nonwovens for filters [J]. Tianjin Textile Science & Technology, 2015(1):16-18.
[15] RAWAL A, SARASWAT H. Pore size distribution of hybrid nonwoven geotextiles[J]. Geotextiles and Geomembranes, 2011, 29(3): 363-367.
[16] PAN N, CHEN J, SEO M, et al. Micromechanics of a planar hybrid fibrous network[J]. Textile Research Journal, 1997, 67(12): 907-925.
