一类特定数字集下自仿测度的非谱性

刘佳惠

(陕西师范大学 数学与信息科学学院,西安 710119)

1 预备知识

设μM,D是由迭代函数系{φd(x)=M-1(x+d)}迭代产生的,Hutchinson在文献[1]中证明该迭代函数系产生的自仿测度μ:=μM,D满足下面等式的唯一概率测度：

其中M∈Mn(Ζ)扩张整数矩阵,D⊂Ζn是基数为|D|的有限数字集,它的支撑是该迭代函数系的吸引子T:=T(M,D).如果存在一个离散的集合Λ⊂Rn,使得指数函数系E(Λ):={e2πi〈λ,x〉:λ∈Λ}构成Hilbert空间L2(μM,D)的正交基(Fourier基),则称自仿测度μM,D为谱测度,上述集合Λ是μM,D的一个谱,也称(μM,D,Λ)为一个谱对(见文献[2],[3]).近年来,自仿测度的谱与非谱以及μM,D-正交指数函数系的有限性与无限性问题已经成为人们研究的主要内容,并取得有效的成果(见文献[9],[12],[13]);而对于非谱问题的研究主要分为两类(见文献[5-7])：(i)空间L2(μM,D)中有有限个正交指数函数系,(ii)空间L2(μM,D)中有无限个正交指数函数系,但不组成正交集.

在平面上，正交指数函数系有限与无限问题已取得比较完善的结论(见文献[9],[12]),在空间上仅对对角矩阵或上(下)三角矩阵进行了研究(见文献[7],[8],[10]).在文献[14]研究的基础上,对于空间上任意三阶扩张矩阵M下面的定理给出了存在无限μM,D-正交指数函数系的充分条件.

定理1.1[14]设D⊂Ζ3是有限数字集,使得

E=E1∪E2∪E3⊆{x∈[0,1)3:mD(x)=0}

(1.1)

其中E1={ek1/2:k1∈{1,2,3}},E2={(ek1+ek2)/2:k1,k2∈{1,2,3}},k1≠k2},E3={(e1+e2+e3)/2}这里e1=(1,0,0)t,e2=(0,1,0)t,e3=(0,0,1)t表示空间R3中的标准正交基.则|D|是一个大于等于8的偶数,且数字“8”是最好的.若M∈M3(Z)为扩张矩阵,使得det(M)∈2Z,则空间L2(μM,D)中存在无限正交系E(Λ)且Λ⊆Z3.

满足(1.1)式的数字集是非常多的,(见[14])而且数字8是最好的下界,并构造出空间R3中一个八元素数字集D

(1.2)

定理1.1中仅讨论了det(M)∈2Z的情况,对于det(M)∈2Z+1的情况,研究其正交指数系的有限性与无限性还有一定的难度和复杂性,但此处数字集的基数|D|是偶数,按照[文献[5],猜想1]可知,空间L2(μM,D)中应该有有限个指数正交系,而在有限性遗留的问题仍然是第一类的问题,即估计空间L2(μM,D)中正交指数函数系的最佳上界.若上述扩张矩阵M为对角矩阵,数字集满足(1.1)式,(i)当p1,p2,p3这三个数中至少有一个数是偶数时,空间L2(μM,D)中存在无限正交系E(Λ)且Λ⊆Z3;(ii)pj∈2Z{0,±1}(j=1,2,3)时,满足条件(1.1)式的数字集D=D1+D2+D3(D1={0,e1},D2={0,e2},D3={0,e3}),则μM,D为谱测度[14].对于定理1.1给出的这类数字集所对应的μM,D-正交指数函数系的有限性问题还未解决.本文主要在上述研究的基础之上讨论det(M)∈2Z+1,研究八元数字集D的谱性质，推广了已有的结果.

2 主要结果及其证明

定理2.1 对于如下形式的三阶扩张矩阵和数字集：

(2.1)

当pj∈2Z+1{0,±1},j=1,2,3,μM,D是非谱测度,且空间L2(μM,D)中正交指数函数系至多包含“8”个,且数字“8”是最好的.

证明对于形如(2.1)式中的M和D,如果λj∈R3(j=1,2,3…,9)是空间L2(μM,D)中存在的九个正交指数函数系,设它们为e2πi<λ1,x>,e2πi<λ2,x>,e2πi<λ3,x>,…,e2πi<λ9,x>,其中

(2.2)

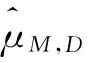
首先由(2.1)式给出的数字集D,这里D=D1⊕D2⊕D3(D1={0,e1},D2={0,e2},D3={0,e3})(见文献[14]),见文献[10]知：

(2.3)

得：

θ0(x)={ξ∈R3:mD(ξ)=0}=A1∪A2∪A3

(2.4)

解得：

(2.5)

(2.6)

(2.7)

这里A1∪A2∪A3可以分成无不相交的集合

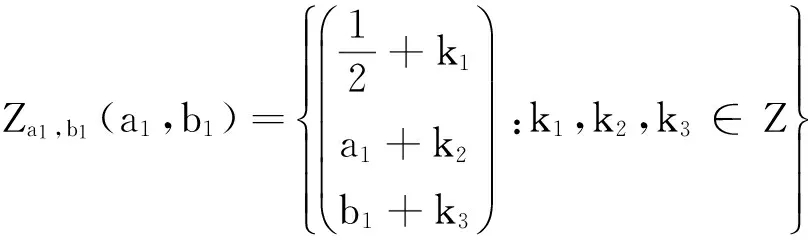
(2.8)

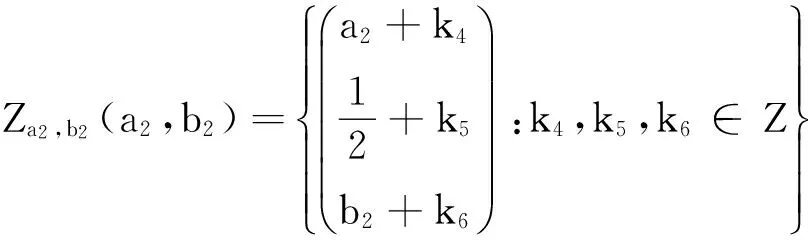
(2.9)

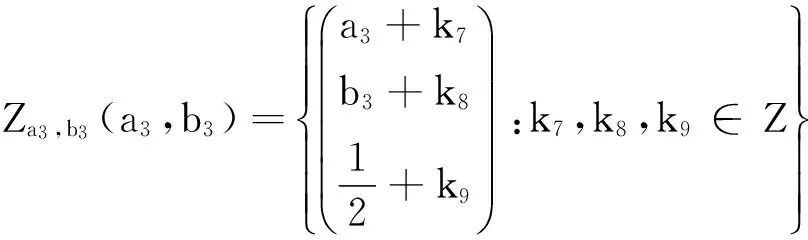
(2.10)

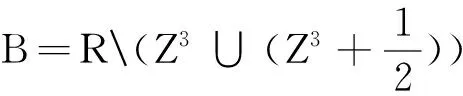
(2.11)

通过式子(2.8),(2.9),(2.10)得到：

(2.12)

接下来有Bj(j=1,2,3…,19)定义如下集合：

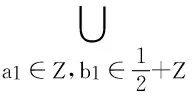
(2.13)

由(2.4)～(2.13)式知：

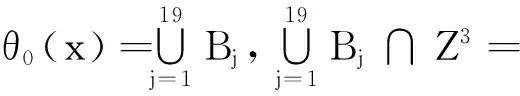
(2.14)

(2.15)

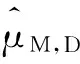
引理2.2 (2.16)式中的Zj(j=1,2,…,19)满足下面的性质：

(1)Z1,Z2,…,Z19互不相交；

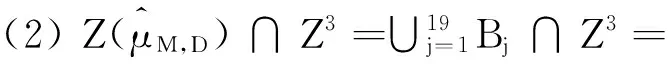
(3)Zj±Zj⊆Z3,Zj=-Zj,(j=1,2,…,7);

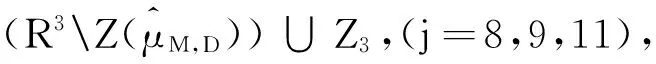
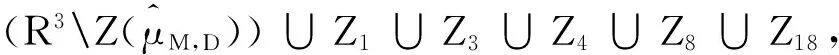
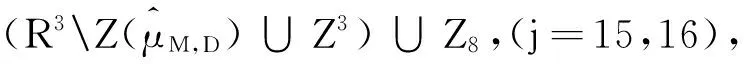
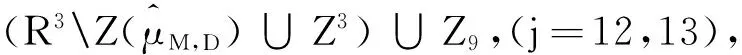
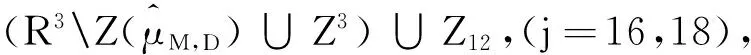
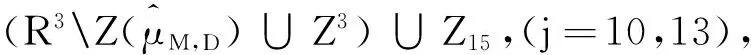
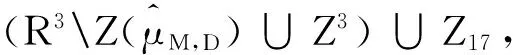
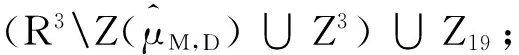
(6)Z1±Zk⊆Zk(k=15,16,17,18,19),

Z2±Zk⊆Zk(k=10,12,13,14,19),

Z3±Zk⊆Zk(k=8,9,11,14,17)；

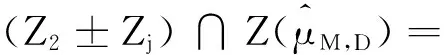
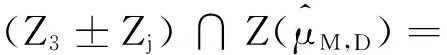
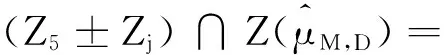
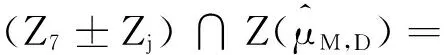
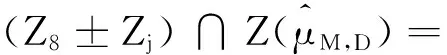
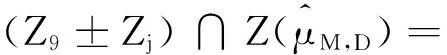
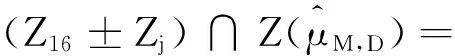
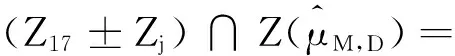
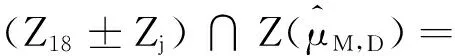
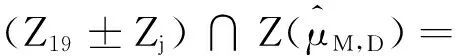
(2.16)

为了证明空间空间L2(μM,D)中正交指数函数系至多包含“8”个,且数字“8”是最好的.接下来分成步骤一,步骤二,步骤三来完成定理的证明.

步骤一证明每个盒子里面至多包含的元素个数.

引理2.3P1至多包含七个元素.λjk-λj∈P1(jk≠j,1≤k≤9,1≤j≤9,jk∈{1,2,…,9})是七个不同的数.

证明首先证明Z1至多包含(2.2)式中的一个元素.设λj1-λj,λj2-λj∈Z1,由引理2.2(3)知

λj1-λj2=(λj1-λj)-(λj2-λj)∈Z1-Z1⊆Z3

(2.17)

引理2.4P2至多包含六个元素.λjk-λj∈P2(jk≠j,1≤k≤9,1≤j≤9,jk∈{1,2,…,9})是六个不同的数.

证明首先证明Z8至多包含(2.2)式中的两个元素.设λj1-λj,λj2-λj,λj3-λj∈Z8,由引理2.2(4),(2.2)式知：

λj1-λj2=(λj1-λj)-(λj2-λj)∈Z8-Z8⟹λj1-λj2∈Z3

(2.18)

λj1-λj3=(λj1-λj)-(λj3-λj)∈Z8-Z8⟹λj1-λj3∈Z3

(2.19)

由引理2.2(3)知：

λj2-λj3=(λj1-λj3)-(λj1-λj2)∈Z3-Z3⊆Z3

(2.20)

综上所述知：六个元素全部包含在Z8∪Z9∪Z11或者Z8∪Z10∪Z11,(2-2-2)分布；五个元素包含在Z8∪Z9∪Z11或Z8∪Z10∪Z11,(2-2-1),(2-1-2),(1-2-2)分布;四个元素包含在Z8∪Z9,Z8∪Z10,Z8∪Z11,Z9∪Z11或Z10∪Z11,(2-2)分布；Z8∪Z9∪Z11或者Z8∪Z10∪Z11,(2-1-1),(1-1-2),(1-2-1)分布；以此类推.

引理2.5P3至多包含四个元素.λjk-λj∈P3(jk≠j,1≤k≤9,1≤j≤9,jk∈{1,2,…,9})是四个不同的数.

证明由引理2.2(4)知：Z10与Z12,Z13有相同的性质,由引理2.4知：Z12,Z13至多包含(2.2)式中的两个元素.其次证明Z14至多包含(2.2)式中的四个元素.设λj1-λj,λj2-λj,λj3-λj,λj4-λj,λj5-λj∈Z14,则λj1-λj2，λj1-λj3，λj1-λj4，λj1-λj5∈Z14-Z14，由引理2.2(4)知可分成如下三种情形

情形1 由引理2.3，(2.2)式知，不妨设λj1-λj2∈Z2,λj1-λj3∈Z3,λj1-λj4∈Z5,则λj1-λj5不属于Z2,Z3,Z5,Z9,Z10.

(i)λj1-λj5∈Z2,由引理2.2(3)知:λj2-λj5=(λj1-λj5)-(λj1-λj2)∈Z2-Z2⊆Z3,

(ii)λj1-λj5∈Z3,由引理2.2(3)知:λj3-λj5=(λj1-λj5)-(λj1-λj3)∈Z3-Z3⊆Z3,

(iii)λj1-λj5∈Z5,由引理2.2(3)知:λj4-λj5=(λj1-λj5)-(λj1-λj4)∈Z5-Z5⊆Z3,

(iv)λj1-λj5∈Z9,由引理2.2(7)知:

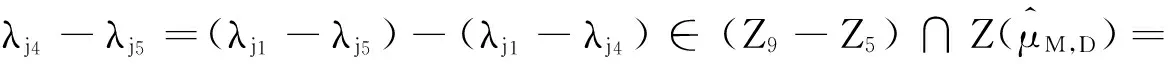
(v)λj1-λj5∈Z10,由引理2.2(7)知:

情形2 由引理2.4知Z9,Z10不能同时包含(2.2)式中的元素,由引理2.2(7)知Z9与Z2,Z5也不能同时包含(1.2)式中的元素,即:λj1-λj2∈Z3,λj1-λj3,λj1-λj4∈Z9,则λj1-λj5不属于Z2,Z3,Z5,Z9,Z10.

(ii)λj1-λj5∈Z3,由引理2.2(3)知:λj2-λj5∈Z3-Z3⊆Z3,

(iv)λj1-λj5∈Z9,由引理2.4知:Z9至多包含(2.2)式中的两个元素.

(v)λj1-λj5∈Z10,由引理2.4知:Z9和Z10不同时包含(2.2)式中两个元素.

情形3 由引理2.4知Z9,Z10不能同时包含(2.2)式中的元素,由引理2.2(7)知Z10与Z3,Z5也不能同时包含(2.2)式中的元素,即:λj1-λj2∈Z2,λj1-λj3,λj1-λj4∈Z10,则λj1-λj5不属于Z2,Z3,Z5,Z9,Z10,类似情形1,情形2的证明过程可推出矛盾.

综上所述知Z14至多包含(2.2)式中的四个元素.

最后证明P3至多包含四个元素.设λj1-λj,λj2-λj,λj3-λj,λj4-λj,λj5-λj∈P4,有两种情况：

情形4 1-1-3设λj1-λj∈Z12,λj2-λj∈Z13,λj3-λj,λj4-λj,λj5-λj∈Z14,

情形5 1-2-2(2-1-2或2-2-1)设λj1-λj∈Z12,λj2-λj,λj3-λj∈Z13,λj4-λj,λj5-λj∈Z14,

情形4由引理2.2(5)，(2.2)式知:λj1-λj3,λj1-λj4,λj1-λj5∈Z9,由引理2.2(4)，(2.2)式知:λj3-λj4,λj3-λj5,λj4-λj5∈Z3,由引理2.2(3)知:λj4-λj5=(λj3-λj5)-(λj3-λj4)∈Z3-Z3⊆Z3与引理2.2(2)矛盾.因此由上述分析可知：P3至多包含四个元素.当Z12或Z13包含(2.2)式中的一个元素,Z14至多包含(2.2)式中的两个元素.

情形5由引理2.2(5)，(2.2)式知:λj2-λj4,λj3-λj4∈Z9,由引理2.2(4)，(2.2)式知:λj2-λj3∈Z9-Z9⟹λj2-λj3∈Z3,λj2-λj3∈Z13-Z13⟹λj2-λj3∈Z2,与引理2.2(1)矛盾.由上述分析可知：P3至多包含四个元素.当Z13(Z12)与Z14包含(2.2)式中的元素,Z13(Z12)至多包含(2.2)式中的一个元素.

综上所述知：P3至多包含四个元素.(1-1-2),(0-0-4),(2-2-0)分布；P3包含三个元素.(1-1-1),(1-2-0),(2-1-0),(1-0-2),(0-1-2),(0-0-3)分布;以此类推.

引理2.6P4至多包含四个元素.λjk-λj∈P3(jk≠j,1≤k≤9,1≤j≤9,jk∈{1,2,…,9})是四个不同的数.由于P3与P4有相同的性质,因此可证得Z15,Z16至多包含(2.2)式中的两个元素.Z17至多包含(2.2)式中的四个元素.P4至多包含四个元素.

引理2.7P5至多包含四个元素.λjk-λj∈P3(jk≠j,1≤k≤9,1≤j≤9,jk∈{1,2,…,9})是四个不同的数.由引理2.2(4)知Z15,Z16与Z18有相同的性质,可证Z18至多包含(2.2)式中的两个元素.Z17与Z19有类似的性质,可证Z19至多包含(2.2)式中的四个元素.P5至多包含四个元素.

步骤二三十六个元素放入五个盒子里面进行分类，分成四类.

步骤三证明空间L2(μM,D)中正交指数函数系至多包含“8”个,且数字“8”是最好的.

情形1(7-1)分布：设λj-λ1∈P1,(2≤j≤8),由引理2.2(7)知：λ9-λ1不属于P2,P3,P4,P5,设λ9-λ1∈Z8,λ9-λ2∈Z1-Z8⊆Z3,与引理2.2(2)矛盾.其他情况可类似证明.

情形2(6-2)分布：由引理2.3,2.4可分成如下两种情况：

情形2.1 设λj-λ1∈P1,(2≤j≤7).

情形2.2 设λj-λ1∈P2,(2≤j≤7).

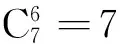
情形2.2设λj-λ1∈P2,(2≤j≤7),由引理2.4可分成如下两种情况：

情形2.2.1 设λ2-λ1,λ3-λ1∈Z8,λ4-λ1,λ5-λ1∈Z9,λ6-λ1,λ7-λ1∈Z11,

情形2.2.2 设λ2-λ1,λ3-λ1∈Z8,λ4-λ1,λ5-λ1∈Z10,λ6-λ1,λ7-λ1∈Z11,

以上两种情况类似，因此下面讨论情形2.2.1的情况即可.由引理2.2(7)知：Z8∪Z9∪Z11与Zj(j=1,2,4,5,6,7,10,12,13,16,18,19)可推出矛盾.则λ8-λ1,λ9-λ1不属于P1,P5,设λ8-λ1,λ9-λ1∈Z14或Z17可分成如下两种情形：

情形2.2.1.1 设λ8-λ1,λ9-λ1∈Z14,

情形2.2.1.2 设λ8-λ1,λ9-λ1∈Z17,

情形2.2.1.1设λ8-λ1,λ9-λ1∈Z14,由引理2.2(5)，(2.2)式知：

λ2-λ8=(λ2-λ1)-(λ8-λ1)∈Z8-Z14⟹λ2-λ8∈Z10

(2.21)

λ3-λ8=(λ2-λ1)-(λ8-λ1)∈Z8-Z14⟹λ3-λ8∈Z10

(2.22)

由引理2.2(4)，(2.2)式知：

λ2-λ3=(λ2-λ8)-(λ3-λ8)∈Z10-Z10⟹λ2-λ3∈Z2

(2.23)

λ2-λ3=(λ2-λ1)-(λ3-λ1)∈Z8-Z8⟹λ2-λ3∈Z3

(2.24)

与引理2.2(1)矛盾.

情形2.2.1.2设λ8-λ1,λ9-λ1∈Z17,由引理2.2(5)，(2.2)式知：

λ4-λ8=(λ4-λ1)-(λ8-λ1)∈Z9-Z17⟹λ4-λ8∈Z18

(2.25)

λ5-λ8=(λ5-λ1)-(λ8-λ1)∈Z9-Z17⟹λ5-λ8∈Z18

(2.26)

由引理2.2(4)知：

λ4-λ5=(λ4-λ8)-(λ5-λ8)∈Z18-Z18⟹λ4-λ5∈Z1

(2.27)

λ4-λ5=(λ4-λ1)-(λ5-λ1)∈Z9-Z9⟹λ4-λ5∈Z3

(2.28)

与引理2.2(1)矛盾.

情形3 (5-3)分布：由引理2.3-2.7可分成如下两种情况：

情形3.1 设λj-λ1∈P1,(2≤j≤6),类似情形2.1，此处不再证明；

情形3.2 设λj-λ1∈P2,(2≤j≤6),由引理2.4可分成如下两种情况：

情形3.2.1λj-λ1∈Z8∪Z9∪Z11,(2≤j≤6),

情形3.2.2λj-λ1∈Z8∪Z10∪Z11,(2≤j≤6),

以上两种情况类似，因此下面讨论情形3.2.1的情况即可.

情形3.2.1.1 设λ2-λ1∈Z8,λ3-λ1,λ4-λ1∈Z9,λ5-λ1,λ6-λ1∈Z11,

情形3.2.1.2 设λ2-λ1,λ3-λ1∈Z8,λ4-λ1∈Z9,λ5-λ1,λ6-λ1∈Z11,

情形3.2.1.3 设λ2-λ1,λ3-λ1∈Z8,λ4-λ1,λ5-λ1∈Z9,λ6-λ1∈Z11,

这三种情况记为(1-2-0-2),(2-1-0-2),(2-2-0-1)分布,后两种分布类似第一种分布，下面考虑情形3.2.1.1.由情形2.2.1分析知：λ7-λ1,λ8-λ1,λ9-λ1∈Z14或Z17可分成如下两种情形：

情形3.2.1.1.1 设λ7-λ1,λ8-λ1,λ9-λ1∈Z14

情形3.2.1.1.2 设λ7-λ1,λ8-λ1,λ9-λ1∈Z17,同情形2.2.1.2类似,由(2.25)-(2.28)式可推出矛盾.

情形3.2.1.1.1λ7-λ1,λ8-λ1,λ9-λ1∈Z14,则λ5-λ7,λ6-λ7∈Z11-Z14，由引理2.2(5)，(2.2)式知：λ5-λ7,λ6-λ7∈Z10,由引理2.2(4)，(2.2)式知：λ5-λ6∈Z10-Z10⟹λ5-λ6∈Z2,λ5-λ6∈Z11-Z11⟹λ5-λ6∈Z3,与引理2.2(1)矛盾.

情形4 (4-4)分布：由引理2.3-2.7可分成如下五种情况：

情形4.1 设λj-λ1∈P1,(2≤j≤5),类似情形2.1，此处不再证明,

情形4.2 设λj-λ1∈P2=Z8∪Z9∪Z10∪Z11,(2≤j≤5),

情形4.3 设λj-λ1∈P3=Z12∪Z13∪Z14,(2≤j≤5),

情形4.4 设λj-λ1∈P4=Z15∪Z16∪Z17,(2≤j≤5),

情形4.5 设λj-λ1∈P2=Z18∪Z19,(2≤j≤5),

情形4.2设λj-λ1∈P2=Z8∪Z9∪Z10∪Z11,(2≤j≤5),由引理2.4知:这种情况有如下11种分布：(1-2-0-1),(2-1-0-1),(1-1-0-2),(1-0-1-2),(1-0-2-1),(2-0-1-1),(2-2-0-0),(2-0-2-0),(2-0-0-2),(0-2-0-2),(0-0-2-2);后面九种类似于情形2.2，情形3.2的证明过程，前面两种分布类似，即讨论(1-2-0-1)，其他情况可类似证明.

情形4.2.1λ2-λ1∈Z8,λ3-λ1,λ4-λ1∈Z9,λ5-λ1∈Z11,由情形2.2.1分析知：λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z14或Z17可分成如下两种情形：

情形4.2.1.1 设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z14

情形4.2.1.2 设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z17,同情形2.2.1.2类似,由(2.25)～(2.28)式可推出矛盾.此处不再证明.

情形4.2.1.1设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z14由引理2.2(5),(2.2)式知λ2-λ7,λ2-λ8,λ2-λ9∈Z8-Z14⟹λ2-λ7,λ2-λ8,λ2-λ9∈Z10,λ7-λ8,λ7-λ9,λ9-λ8∈Z10-Z10，由引理2.2(4),(2.2)式知λ7-λ8,λ7-λ9,λ9-λ8∈Z2，由引理2.2(3)知λ9-λ8∈Z2-Z2⊆Z3,与引理2.2(2)矛盾.

情形4.3 设λj-λ1∈P3=Z12∪Z13∪Z14,(2≤j≤5),由引理2.5知:这种情况有如下3种分布：(1-1-2),(2-2-0),(0-0-4);前两种情况类似,讨论(1-1-2),(0-0-4)即可，其他情况可类似证明.

情形4.3.1 设λ2-λ1∈Z12,λ3-λ1∈Z13,λ4-λ1,λ5-λ1∈Z14,

情形4.3.2 设λ2-λ1,λ3-λ1,λ4-λ1,λ5-λ1∈Z14,

情形4.3.1由引理2.2(7)知：Z12∪Z13∪Z14与Zj(j=1,4,6,7,8,11,15,16,17,18)可推出矛盾，则λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1不属于P1,P2,P4.设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z19,则λ3-λ7,λ3-λ8,λ3-λ9∈Z13-Z19,由引理2.2(5),(2.2)式知λ3-λ7,λ3-λ8,λ3-λ9∈Z15,由引理2.2(4),(2.2)式知λ7-λ8,λ7-λ9∈Z15-Z15⟹λ7-λ8,λ7-λ9∈Z1,由引理2.2(3)知λ9-λ8=(λ7-λ8)-(λ7-λ9)∈Z1-Z1⊆Z3,与引理2.2(2)矛盾.

情形4.3.2由引理2.2(7)知:Z14与Zj(j=1,4,6,7,15,16,18)可推出矛盾，则λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1不属于P1.设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈P2,同情形4.2的11种分布，均可推出矛盾.则λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈P4或P5,可分成两种情况：

情形4.3.2.1 设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z17,

情形4.3.2.1 设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z19,

以上两种情况类似，因此下面讨论情形4.3.2.1的情况即可.

λ2-λ3=(λ2-λ1)-(λ3-λ1)=(λ2-λ6)-(λ3-λ6)∈Z2,

(2.29)

λ2-λ4=(λ2-λ1)-(λ4-λ1)=(λ2-λ6)-(λ4-λ6)∈Z2,

(2.30)

由引理2.2(3)知：

λ3-λ4=(λ2-λ4)-(λ2-λ3)∈Z2-Z2⊆Z3,

(2.31)

与引理2.2(2)矛盾.

情形4.4λj-λ1∈P4=Z15∪Z16∪Z17,(2≤j≤5),由引理2.6知:这种情况有如下3种分布：(1-1-2),(2-2-0),(0-0-4);前两种情况类似,第三种情形同情形4.2,情形4.3中的情况类似，可推出矛盾,讨论(1-1-2)分布即可,设λ2-λ1∈Z15,λ3-λ1∈Z16,λ4-λ1,λ5-λ1∈Z17,由引理2.2(7)知：Z15∪Z16∪Z17与Zj(j=2,5,6,7,9,10,11,12,13,14)可推出矛盾,则λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1不属于P1,P2,P4.由引理2.7知：设λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈Z19,由引理2.2(5),(2.2)式知：λ3-λ6,λ3-λ7,λ3-λ8∈Z16-Z19⟹λ3-λ6,λ3-λ7,λ3-λ8∈Z12,由引理2.2(4),(2.2)式知：λ6-λ7,λ6-λ8∈Z12-Z12⟹λ6-λ7,λ6-λ8∈Z2,由引理2.2(3)知：λ7-λ8=(λ6-λ8)-(λ6-λ7)∈Z2-Z2⊆Z3,与引理2.2(2)矛盾.

情形4.5λj-λ1∈P4=Z18∪Z19,(2≤j≤5),由引理2.7知:λ2-λ1,λ3-λ1,λ4-λ1,λ5-λ1∈Z19,由引理2.2(7)知:Z19与Zj(j=3,4,5,7,8,9,11)可推出矛盾，则λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1不属于P1,P2.即λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈P3=Z12∪Z13∪Z14,类似情形4.3的情形可推出矛盾；λ6-λ1,λ7-λ1,λ8-λ1,λ9-λ1∈P4=Z15∪Z16∪Z17,类似情形4.3的情形可推出矛盾.

综上证明可知：当pj∈2Z+1{0,±1},j=1,2,3,μM,D是非谱测度,且空间L2(μM,D)中至多有8个正交指数函数系,进一步地，可以得到很多包含8个正交指数函数的集合.例如指数函数系E(S)就是空间L2(μM,D)中含有8个相互正交的指数函数系，其中

从而可知数字“8”是最好的,证毕.

2 结语

[1] HUTCHINSON J E.Fractals and self-similarity[J].Indiana Univ.Math.J.1981,30:713-747.

[2] JORGENSEN P E T,PEDERSEN S.Dense analytic subspaces in fractalL2-spaces[J].J.Anal.Math,1998,75:185-228.

[3] JORGENSEN P E T,PEDERSEN S.Spectral pairs in Cartesian coordinates[J].J.Fourier.Anal.Appl,1999,5:285-302.

[4] DUTKAY D E,JORGENSEN P E T.Analysis of orthogonality and of orbits in affine iterated function systems[J].Math.Z,2007,256:801-823.

[5] LI J L.Non-spectral problem for a class of planar self-affine measures[J].J.Funct.Anal,2008,255:3125-3148.

[6] LI J L.Non-spectral of planar self-affine with three-element digit set[J].J.Funct.Anal,2009,257:537-552.

[7] LI J L.The cardinality of certainμM,D﹣orthogonal exponentials[J].J.Math.Anal.Appl,2010,362:514-522.

[8] LI J L.Non-spectral of self-affine measures on the spatial Aoerpinski[J].J.Math.Anal.Appl,2015,432:1005-1017.

[9] LI J L.On theμM,D- orthogonal exponentials[J].Nonlinear. Analysis,2010,73:940-951.

[10] LI J L.Spectrality of self-affine measures on the three-dimensional Sierpinski gasket[J].Proc.Edinburgh.Math,2012,55:477-496.

[11] LI J L.Spectrality of class of self-affine measures with decomposable digit sets[J].Sci.China.Math,2012,55(12):1229-1242.

[12] LI J L.Analysis ofμM,D-orthogonal exponentials for the planar four-element digit sets[J].Math.Nachr,2014,287:297-312.

[13] LI J L.A necessary and sufficient condition for the finiteμM,D-orthogonality[J].Sci.Math,2015,58(12):2541-2548.

[14] 李敏.空间自仿测度下无限正交指数系存在的条件[J].数学进展，2016,45(3):332-342.