分析在空调系统运行优化中的可行性研究

黄婷婷 梁彩华 张小松

（东南大学能源与环境学院 南京 210096）

随着经济发展和人们生活水平的提高，空调能耗在建筑能耗中所占比重日益增加。据统计，空调运行能耗约占建筑总能耗的50% ～60%［1］，因此空调系统运行节能成为降低建筑总能耗的重要途径之一。常规空调系统的设计选型是以建筑最大负荷为依据，而实际上空调系统90%以上的运行时间都处于70%设计负荷以下波动运行［2］，由此造成空调系统运行效率降低，能源浪费严重。因此，对空调系统进行准确的能效评价，并采取有效的优化措施是保证空调系统在部分负荷下高效运行的重要条件。

目前，空调系统优化研究方法主要包括能效分析法和“ ”分析法。能效分析法采用一些常规的能效评价指标包括日本空调系统能耗系数CEC（coefficient of energy consumption）、美国 IPLV（integrated part load value）评价指标、制冷机组制冷系数COP（或EER）、制冷机组季节能效比SEER、采暖季节性能系数HSPF等对空调系统整体性能进行评价。但能效分析法主要从能源的数量上对空调系统进行评价，尚缺乏从能源的数量和品位两方面对系统进行研究。为此，有学者提出用“ ”分析方法对空调系统进行能效评价［3-5］。“ ”分析通过研究能量中 的传递、转化、利用和损失的情况，进而确定系统的 利用效率，其核心内容在于热功转换［6］。然而对于空调系统而言，营造空调房间的建筑热湿环境最核心的工作是将室内多余热量和湿量排除到室外，并不以热功转换为目的。 分析的基础是研究对象与环境温度（参考温度）之间的差异形成的做功能力，与建筑热湿环境营造过程的核心工作不一致［6］。

Guo Zengyuan等［7］基于热电比拟，提出了一个新的传热物理量—— ， 具有物体热量的“能量”性质，代表物体传递热量的总能力，对于内能为U，温度为T的物体，其 定义为G＝1/2UT。由于热量传递过程的不可逆性，传热过程必然伴随着 的耗散，Guo Zengyuan等［7］发展了表征当量热阻的 耗散极值原理，将 理论应用于优化导热、对流、辐射等多种传热过程［8-10］。为更直观地表示 在传热过程中的变化规律，Chen Qun等［11］建立了传热过程的T-q图，并用于换热系统的优化分析。对于热功转换过程，Cheng Xuetao等［12-14］进一步发展了 理论并基于功

和 耗散的概念提出 损失的概念，将 损失定义为流入与流出系统的 流之差，也表明 损失等于功

和 耗散之和，使得既有传热又有热功转换的热力学过程优化成为可能。

分析在传热和热功转换优化过程中有良好的适用性［15-17］，考虑到空调系统运行同样包括蒸发、冷凝等换热过程和压缩制冷等功-热转换过程，因此本文将 理论应用于空调系统优化运行中，提出空调系统 增加极值原理，构建空调系统的 增加率模型，通过实验研究，探索 理论在评价空调系统能效方面的可行性，为实现空调系统的整体节能优化运行提供了新思路。

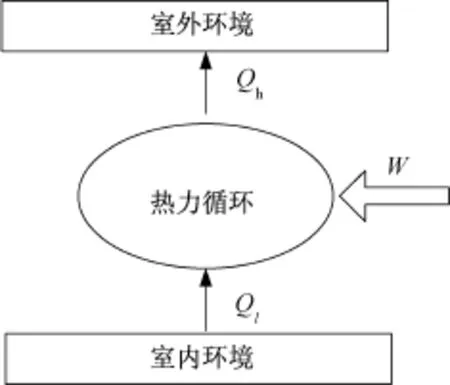
图1 空调系统能量转换Fig.1 Energy conversion in air conditioning systems

1 空调系统 增加极值原理

根据空调系统能量守恒：

其中：

式中：Qh，Ql分别为高，低温热源与工质之间的换热量，kW；W，Wc，Wdp，Wqp分别为系统输入功率，压缩机功率，冷冻水泵功率和冷却功率，kW。

在空调系统中 的变化主要包括：1）不可逆传热引起的 耗散；2）主要功耗设备（包括压缩机、冷冻水泵和冷却水泵）做功引起系统 增加而产生的功 。

高低温热源与工质传热所引起的 损失率表示为［7］：

式中：Gl，Gh分别为低，高温热源与工质传热引起的 损失率，kW·k；Tl，Th分别为低，高温热源温度，K；ql，qh分别为工质与低，高温热源的热通量，kW/m2；Al，Ah分别为工质与低，高温热源的换热面积，m2。

根据热力学第一定律，推导得到热力循环过程平衡方程为［12］：

式中：Gm为工质的 ，kW·K。由于工质的 是一个状态参数，经历一个循环后将回到初始状态，因此：

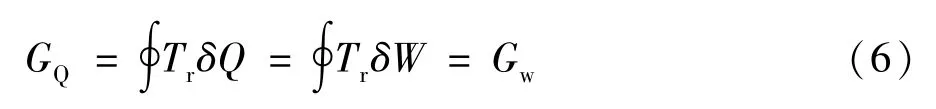
式中：GQ，GW分别为工质在热力学循环中传热引起的 损失率和做功引起的 损失率，kW·K。

由于：

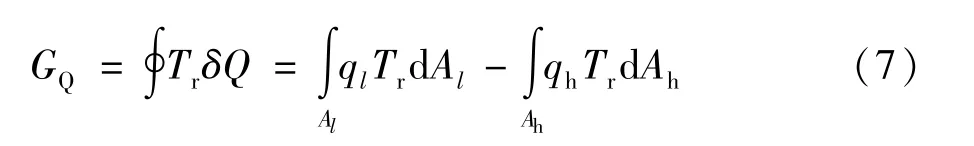
所以：

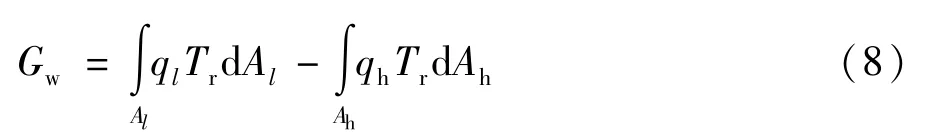
空调系统的 损失率为工质与高低温热源传热引起的的 损失率和工质在热力学循环中做功引起的 损失率之和，结合式（3）、式（4）、式（8）可得：

由于Ql、Th和W都为正值，且Th大于Tl，所以系统 损失率始终为负值，即系统 不但没有减少，而且是增加的。

将空调系统 增加率表示为：

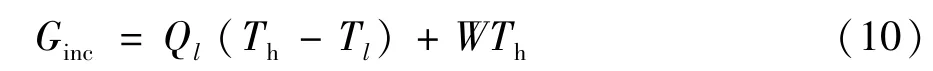
由式（10）可知，给定高低温热源温度时，当系统制冷量一定，系统 增加率最小时，系统输入功率最小，系统效率最高；当系统输入功率一定，系统 增加率最大时，系统制冷量最大，系统效率最高，这就是空调系统 增加极值原理。

2 空调系统 增加模型

空调系统由冷水机组、冷却塔、末端和管道组成。本文将分别构建压缩机、冷凝器、蒸发器、冷却塔、表冷器、冷冻水泵、冷却水泵、风机及管道的 损失率计算模型，最后形成整个空调系统的 变化模型。

2.1 压缩机 损失率模型

首先对模型的建立作如下假设：压缩机的压缩过程绝热。由于压缩机可视为一个开口热力学系，采用开口热力学的 平衡方程对其进行分析，压缩机的输入功用来增加制冷剂的 ，则压缩机过程 损失率为：

式中：mr为制冷剂质量流量，kg/s；H1，H2分别为压缩机吸气焓和排气焓，kJ/kg；Tci，Tco分别为压缩机的吸排气温度，K。

2.2 冷凝器 损失率模型

图2所示为冷凝器内整个传热过程的T-q图。将传热过程分为3段：过热段、冷凝段、过冷段。在制冷剂与冷却水的传热过程中因传热的不可逆性不可避免地将发生 损失，上下两条线分别表示制冷剂与冷却水温度的变化规律，整个传热过程总的传热量为Qh，而两条线之间区域的面积即为在传热过程中发生的 损失。

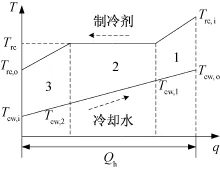
图2 冷凝器传热过程T-q图Fig.2 T-q diagram for heat transfer in the condenser

冷凝器内由传热引起的 损失率表示为：

式中：Qc1，Qc2，Qc3分别为过热段、冷凝段和过冷段的换热量，kW；Tri，i，Trc，Trc，o分别为冷凝器进口制冷剂温度，冷凝温度和冷凝器出口制冷剂温度，K；Tcw，i，Tcw，1，Tcw，2，Tcw，o分别为冷凝器进口冷却水温，过热段出口冷却水温，冷凝段出口冷却水温和冷凝器出口冷却水温，K。

2.3 蒸发器 损失率模型

图3所示为蒸发器内整个传热过程的T-q图。将传热过程分成两段：过热段和蒸发段。与冷凝器一样，蒸发器内存在由传热引起的 损失。

图3 蒸发器传热过程T-q图Fig.3 T-q diagram for heat transfer in the evaporator

蒸发器内由传热引起的 损失率表示为：

式中：Qe1，Qe2分别为蒸发段和过热段的换热量，kW；Tw，i，Tw，o，Tw，1分别为蒸发器进口冷冻水温，出口冷冻水温和过热段出口冷冻水温，K；Tre，Tre，o分别为蒸发温度和蒸发器出口制冷剂温度，K。

2.4 冷却塔 损失率模型

从冷凝器流出的高温冷却水进入冷却塔内与空气发生热湿交换，这时空气被加热加湿，因此空气与冷却水之间不仅存在显热交换还存在潜热交换。

冷却塔内空气与冷却水显热交换引起的 损失率表示为：

式中：Qa1为空气与冷却水的显热换热量，kW；Ta，i，Ta，o分别为空气进塔温度和出塔温度，K；Twt，i，Twt，o分别为冷却水进塔温度和出塔温度，K。

由于空气和冷却水之间潜热交换引起的湿 损失率为：

式中：ma为空气质量流量，kg/s；da，i，da，o分别为空气进塔绝对含湿量和出塔绝对含湿量，g/kg。

将湿 损失率转换为显热 损失率［18］：

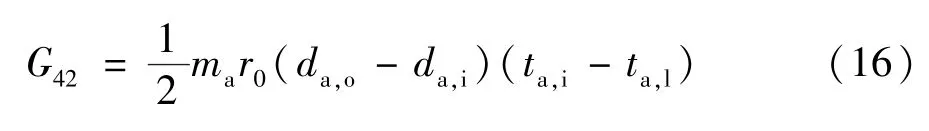
式中：r0为水蒸汽的汽化潜热，kJ/kg；ta，l为进塔空气对应的露点温度，K。

根据式（14）和式（16）得到空调系统 损失率为：

2.5 表冷器 损失率模型

表冷器内被冷却空气与冷冻水换热引起 损失，表示为：

式中：Qn为空气与冷冻水的换热量，kW；Tn，i，Tn，o分别为空气进出表冷器温度，K；Twb，i，Twb，o分别为冷冻水进出表冷器温度，K。

2.6 水泵 损失率模型

冷冻水泵和冷却水泵均为流体的输送设备，其输入功用于克服流体的黏性阻力耗散，做功导致流体的

增加。其 损失率分别为：

2.7 管道 损失模型

除了传热不可逆性引起的 耗散，流体流动过程中流动阻力的存在使得压力发生改变同样会造成工质

耗散。若流体流动是稳态绝热的，焓的变化对熵产的影响可忽略不计，由热力学熵和 的联系可得［16］：

因流体阻力引起的 耗散为［16］：

管道主要包括冷冻水管道和冷却水管道。

冷冻水管道和冷却水管道内的水为不可压缩流体，由流动阻力引起的 损失率分别表示为［16］：

式中：mcw，mw分别为冷却水和冷冻流量，kg/s；Δpcw，Δpw分别为冷却水管路和冷冻水管路压差，kPa；ρcw，ρw分别为冷却水和冷冻水密度，kg/m3。

综上所述，得到空调系统 损失率为：

式中：G1、G6、G7均为负值，且绝对值大于G2、G3、G4、G5、G8、G9之和，因此，空调系统的 增加率表示为：

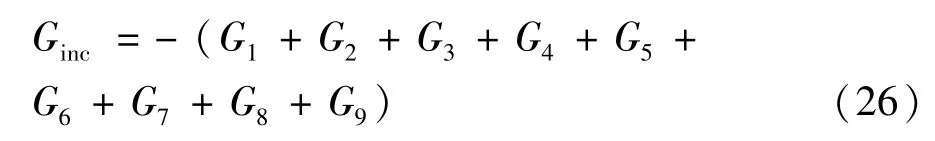
式（26）即空调系统 增加率方程，下文将用此方程对实验机组运行过程中的空调系统 增加率进行计算。

3 理论评价空调系统能效的可行性

为研究在空调系统运行中，系统 增加在评价空调系统能效方面的可行性，本文采用定系统制冷量和定系统输入功率为前提条件，通过调节各运行参数对空调系统不同运行工况下研究了 增加率。

3.1 实验装置

为研究实际空调系统在不同工况下的运行性能，搭建了空调系统综合性能实验系统，如图4所示。系统采用全封闭型旋转式变频压缩机，使用R22制冷剂，频率变化范围为30～110 Hz。冷凝器与蒸发器均为板式换热器，其中冷凝器传热面积为2.04 m2，蒸发器传热面积为1.08 m2。节流装置为热力膨胀阀。冷却塔为逆流开式冷却塔，额定水流量为10 m3/h，额定风量为135 m3/min。空气干湿球温度与水温测量均采用铂电阻温度传感器，测量范围-200～500℃，测量偏差±0.15℃。冷冻水与冷却水流量测量采用涡轮流量计，量程0.6～6 m3/h，精度为1.0%。冷水机组蒸发压力与冷凝压力测量采用压阻型压力变送器，根据测压范围不同，量程分为0～1.5 MPa型和0～2.0 MPa型，测量精度均为0.1%FS。压缩机、水泵功率采用WT230数字功率表，测量精度为0.1%。系统数据采集采用Agilent34970A型数据采集仪。

3.2 实验结果分析

3.2.1 定系统制冷量条件下系统 增加率分析

当室内外空气温度一定时，通过压缩机、冷冻水泵和冷却水泵的变频调节，使空调系统制冷量为5 kW，符合系统制冷量为5 kW的运行工况，参数如表1所示。

图4 空调系统运行性能实验装置系统Fig.4 The experiment platform of the air conditioning system for testing its operating performance

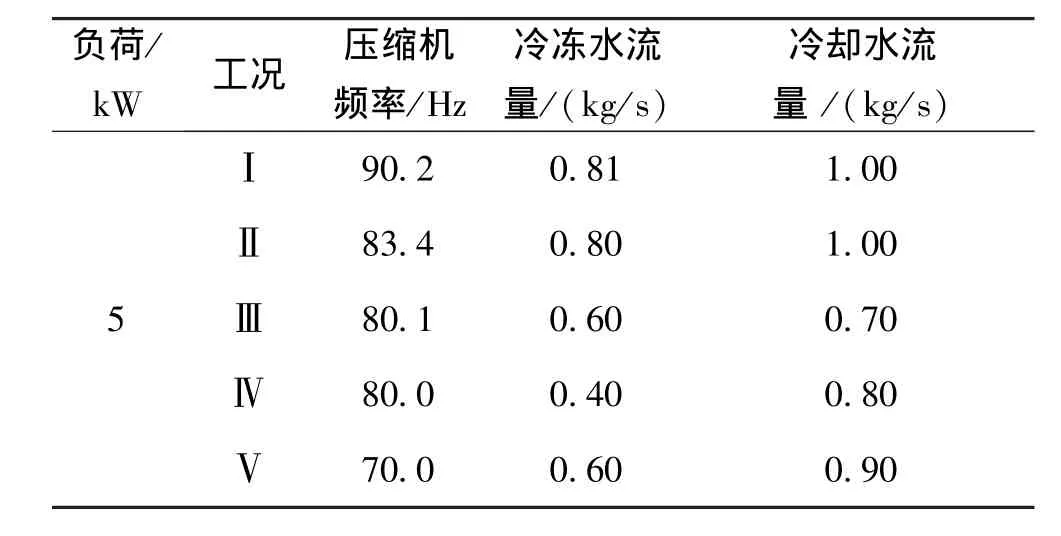
表1 定制冷量空调系统运行工况参数Tab.1 The operating parameters of the air conditioning system in fixed load

图5为定系统制冷量5 kW时，空调系统 增加率与总输入功率在不同运行工况下的实验结果对比。由图5可知，当空调系统在给定制冷量条件下运行时，不同运行工况所对应的空调系统 增加率和总输入功率呈现相同的变化规律，当系统 增加率越小时，系统输入功率也越小，系统效率越高，较好的验证了空调系统 增加极值原理。实验中，当空调系统在运行工况5，即压缩机频率为70 Hz，冷冻水流量为0.6 kg/s，冷却水流量为0.9 kg/s时，系统 增加率最小，系统总输入功率也最小，系统能效最高，因此该工况为实验空调系统在5 kW定制冷量运行时的最佳运行工况。

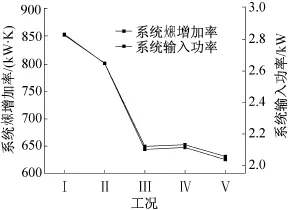
图5 定制冷量5 kW系统 增加率与输入功率变化Fig.5 The correlation between total entransy increase rate and total power consumption for system cooling load fixed 5 kW

3.2.2 定系统输入功率条件下系统 增加率分析

实验中，当室内外空气温度一定时，通过压缩机、冷冻水泵和冷却水泵的变频调节，使空调系统输入功率为2.8 kW，符合系统输入功率为2.8 kW的运行工况参数如表2所示。

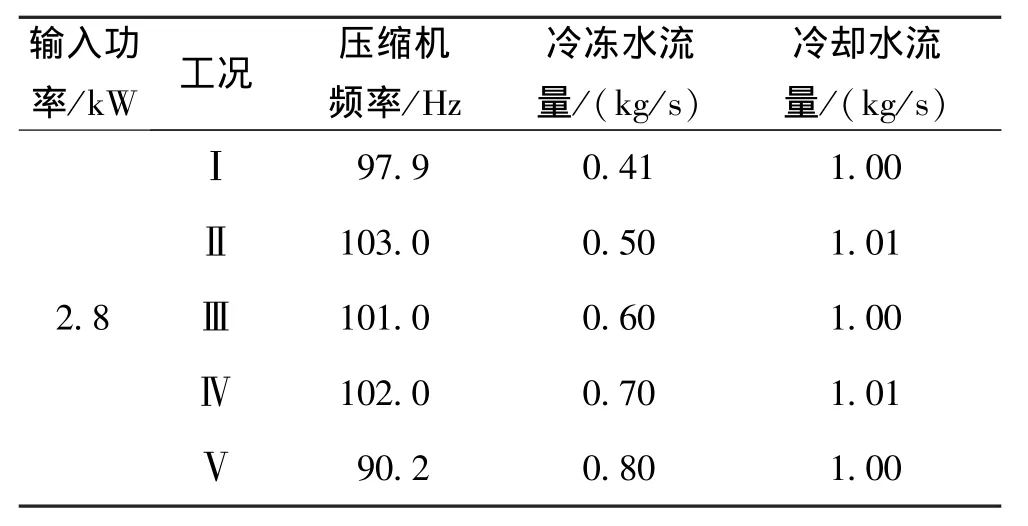
表2 定输入功率空调系统运行工况参数Tab.1 The operating parameters of the air conditioning system in fixed power consumption

图6所示为定输入功率2.8 kW时，空调系统增加率与制冷量在不同运行工况下的实验结果对比。由图6可知，当空调系统在给定制冷量条件下运行时，不同运行工况所对应的空调系统 增加率和制冷量的变化规律呈现较好的一致性，当系统 增加率越大时，系统制冷量也越大，系统效率越高，较好的验证了空调系统 增加极值原理。实验中，当空调系统在运行工况Ⅰ，即压缩机频率＝97.9 Hz，冷冻水流量＝0.41 kg/s，冷却水流量＝1.00 kg/s时，系统 增加率最大，系统制冷量也最大，系统能效最高，因此该工况为实验空调系统在2.8 kW定输入功率运行时的最佳运行工况。

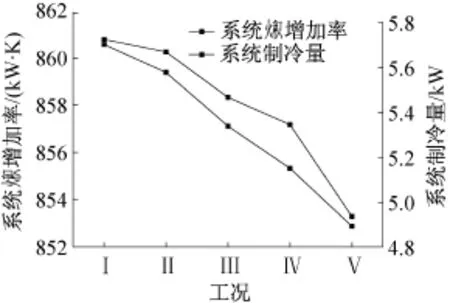
图6 定输入功率2.8 kW系统 增加率与制冷量变化Fig.6 The correlation between total entransy increase rate and cooling load for system power consumption fixed 2.8 kW

4 结论

1）基于 理论，提出空调系统 增加极值原理，指出给定系统制冷量时，系统 增加率最小对应的系统输入功率最小，系统效率最高；给定系统输入功率时，系统 增加率最大对应的系统制冷量最大，系统效率最高。

2）分别构建了空调系统中压缩机、冷凝器、蒸发器、表冷器、水泵和管道的 损失率计算模型，得到空调系统 增加率计算模型。

3）根据定系统制冷量条件下空调系统 增加率与输入功率的实验结果对比，以及定系统输入功率条件下空调系统 增加率与制冷量的实验结果对比，均较好的验证了空调系统 增加极值原理。当系统制冷量＝5 kW时，最佳运行工况为压缩机频率＝70 Hz，冷冻水流量 ＝0.6 kg/s，冷却水流量 ＝0.9 kg/s；当系统输入功率＝2.8 kW时，最佳运行工况为压缩机频率＝97.9 Hz，冷冻水流量＝0.41 kg/s，冷却水流量 ＝1.00 kg/s。

［1］钟玮.我国建筑中央空调能耗现状及全面节能措施［D］.重庆：重庆大学，2004.（ZHONG Wei.The current situation of the energy consumption and total energy conserving methods of central air-conditioner in Chinese building［D］.Chongqing：Chongqing University，2004.）

［2］YU F W，CHAN K T.Improved energy performance of air cooled centrifugal chillers with variable chilled water flow［J］.Energy Conversion and Management，2008，49（6）：1595-1611.

［3］王厉.基于（ ）方法的暖通空调系统热力学分析研究［D］.长沙：湖南大学，2012.（WANG Li.Thermodynamic analysis of HVAC systems based on exergy method［D］.Changsha：Hunan University，2012.）

［4］BACCOLI R，MASTINO C，RODRIGUEZ G.Energy and exergy analysis of a geothermal heat pump air conditioning system［J］.Applied Thermal Engineering，2015，86： 333-347.

［5］DU Zhimin，JIN Xinqiao，FAN Bo.Evaluation of operation and control in HVAC （heating，ventilation and air conditioning）system using exergy analysis method［J］.Energy，2015，89： 372-381.

［6］孟妮.中央空调系统能效评价方法研究［D］.长沙：中南大学，2012.（MENG Ni.The study of the evaluation method of the central air conditioning system energy efficiency［D］.Changsha： Central South University，2012.）

［7］GUO Zengyuan，ZHU Hongye，LIANG Xingang.Entransy-A physical quantity deseribing heat transfer ability ［J］.International Journal of Heat and Mass Transfer，2007，50（13/14）： 2545-2556.

［8］XIA Shaojun，CHEN Lingen，SUN Fengrui.Entransy dissipation minimization for liquid-solid phase change processes［J］.Science China（Technological Sciences），2010，53（4）： 960-968.

［9］CHEN Qun，REN Jianxun，MENG Ji′an.Field synergy equation for turbulent heat transfer and its application［J］.International Journal of Heat and Mass Transfer，2007，50（25/26）： 5334-5339.

［10］CHENG Xuetao，LIANG Xingang.Entransy flux of thermal radiation and its application to enclosures with opaque surfaces［J］.International Journal of Heat and Mass Transfer，2011，54（1/2/3）： 269-278.

［11］CHEN Qun，XU Yunchao，GUO Zengyuan.The property diagram in heat transfer and its applications［J］.Chinese Science Bulletin，2012，57 （35）：4646-4652.

［12］CHENG Xuetao，LIANG Xingang.Entransy loss in thermodynamic processes and its application ［J］.Energy，2012，44（1）： 964-972.

［13］CHENG Xuetao，WANG Wenhua，LIANG Xingang.Optimization of heat transfer and heat-work conversion based on generalized heat transfer law ［J］.Science China Technological Sciences，2012，55（10）： 2847-2855.

［14］CHENG Xuetao，WANG Wenhua，LIANG Xingang.Entransy analysis of open thermodynamic systems［J］.Chinese Science Bulletin，2012，57（22）： 2934-2940.

［15］李孟寻，郭江峰，许明田，等.（ ）耗散理论在管壳式换热器优化设计中的应用［J］.工程热物理学报，2010，31（7）： 1189-1192.（LI Mengxun，GUO Jiangfeng，Xu Mingtian，et al.Application of entransy dissipation theor in optimization design of shell-and-tube heat exchanger［J］.Journal of Engineering Thermophysics，2010，31（7）： 1189-1192.）

［16］许明田，程林，郭江峰.（ ）耗散理论在换热器设计中的应用［J］.工程热物理学报，2009，30（12）：2090-2092.（XU Mingtian，CHENG Lin，GUO Jiangfeng.An application of entransy dissipation theory to heat exchanger design［J］.Journal of Engineering Thermophysics，2009，30（12）： 2090-2092.）

［17］程雪涛，梁新刚.（ ）理论在热功转换过程中的应用探讨［J］. 物理学报，2014，63（19）： 40-47.（CHENG Xuetao，LIANG Xingang.Discussion on the application of entransy theory to heat-work conversion processes［J］.Acta Physica Sinica，2014，63（19）： 40-47.）

［18］谢晓云，江亿.蒸发冷却制备冷水流程的热学分析［J］.暖通空调，2011，41（3）：65-76.（XIE XiaoYun，JIANG Yi.Thermological analysis of chilled water by evaporative cooling processes［J］.Heating Ventilating and Air Conditoning，2011，41（3）： 65-76.）