基于热弹耦合的齿轮热刚度研究

罗彪，李威，李林升



基于热弹耦合的齿轮热刚度研究

罗彪1, 2，李威1，李林升2

(1. 北京科技大学 机械工程学院，北京，100083；2. 南华大学 机械工程学院，湖南 衡阳，421001)

为研究热对齿轮刚度的影响，引入齿轮热刚度的概念，并定义热刚度的计算方法。引入热应力修正系数te，对热应力进行修正，得到热弹耦合应力的计算方法和热弹耦合变形的计算方法。在热弹耦合条件下，分别利用有限元法和解析法计算出齿轮的单齿热刚度和啮合热刚度，2种方法的计算结果基本吻合。研究结果表明：齿轮在热弹耦合作用下的热刚度为齿轮的弹性刚度与修正的热膨胀刚度的串联。齿轮啮合热刚度相对于弹性啮合刚度整体下降，单齿热刚度与弹性刚度沿啮合线的分布曲线在齿根附近存在唯一交点，单齿热刚度在交点的齿根侧大于弹性刚度，在交点的齿顶侧小于弹性刚度。

热弹耦合; 热刚度; 齿轮; 有限元法; 解析法

齿轮的啮合刚度是研究齿轮传动承载能力、传动误差、齿廓修形和动力学特性等的基础，因此，齿轮的刚度研究是齿轮传动研究的热点。研究齿轮刚度的方法包括解析法[1−3]、有限元法[4−6]和实验研究方法[7−9]等。解析法又包括国际标准方法、当量齿形法(石川模型)[10]和势能法[11]等。在各种解析法中，当量齿形法应用最为广泛，而且研究者们基于石川模型提出了很多齿轮啮合刚度的改进算法[12]。同时，很多研究者对齿轮刚度的影响因素也进行了大量研究，主要集中在齿轮的几何参数[13]、齿根裂纹[14]、齿面摩擦因数[15]、齿形误差[16]、磨损及修形[17−18]等。但以上计算方法均未考虑热对齿轮刚度的影响。本文作者基于有限元和石川模型，考虑热对齿轮刚度的影响，引入齿轮热刚度的概念，并给出其具体的计算方法。

1 齿轮热刚度的定义

齿轮在啮合的过程中产生热膨胀，热膨胀的方向与齿轮受外载荷产生的弹性变形的方向相反，能够减少齿轮总的弹性变形量。但在实际工况中，弹性变形和热膨胀是相互影响的，啮合齿轮最终的热弹耦合变形总量大于单独的弹性变形量。这是因为在啮合的过程中由于热膨胀，在啮合点处将产生附加热应力，同时热应力与弹性应力相互耦合产生附加的热弹耦合应力，在弹性应力、热应力和热弹耦合应力的共同作用下，啮合点的实际热弹耦合变形总量要比单独的弹性变形量大。同时，由于温度升高，齿轮材料的弹性模量也发生变化，进一步削弱齿轮的抗变形能力。本文作者引入齿轮热刚度的概念，定义如下：齿轮热刚度为引起单位热弹耦合变形量的外载荷大小。其计算公式为

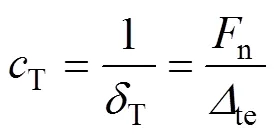
式中：T为齿轮热刚度；T为齿轮热柔度；n为啮合点法向外载荷；te为啮合点法向热弹耦合变形量。

根据以上定义，计算齿轮热刚度的关键在于找到计算啮合点热弹耦合变形量的方法。本文将采用解析法和有限元法分别进行计算。

2 齿轮热刚度的解析法

2.1 基于石川模型的齿轮弹性刚度

齿轮啮合刚度的石川模型是将齿轮齿廓简化成由梯形和矩形组成的当量齿形，再通过材料力学和弹性力学理论来计算当量齿形在外载荷作用下的各个柔度，并根据柔度与刚度的关系求出单齿和啮合齿轮对的刚度。其具体的计算方法参见参考文献[19]。

2.2 齿轮热膨胀

齿轮齿廓热膨胀量的计算方法参见文献[20]。齿廓热膨胀示意图如图1所示。渐开线齿廓上任一点热膨胀后到达′点，在圆柱坐标系下，′点半径r′=r+Δr。r′与轴的夹角φ′=φ+Δφ。其中Δr，φ和Δφ的计算公式分别如下：

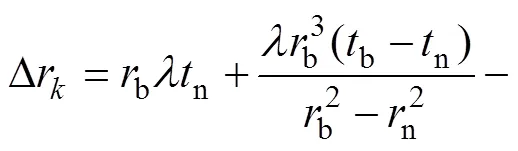
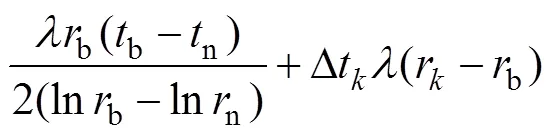
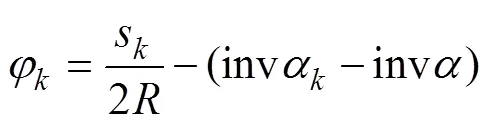
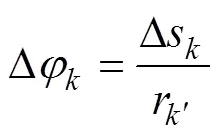
式中：sk为k点的齿厚；Δtk为k点的温升；tn为齿轮内孔表面温度；tb为齿轮基圆温度；φk为k点的半径与y轴夹角；R为齿轮分度圆半径；rb为基圆半径；rn为齿轮内孔半径；αk为k点压力角，invαk为αk对应的展角，invαk=tanαk−αk；α为分度圆压力角，invα为α对应的展角，invα=tanα−α；Δsk为k点周向膨胀量，Δsk=Δtkλsk/2。

由以上分析可知：在直角坐标系下，啮合点热膨胀量沿坐标轴的分量Δ和Δ，以及沿啮合线方向的热膨胀量t计算公式分别为

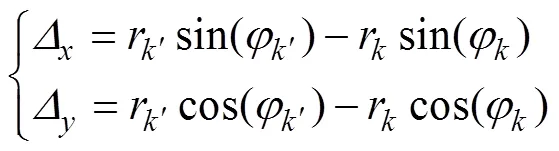
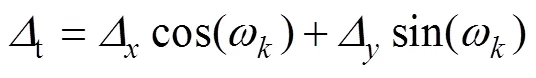
式中：ω为啮合点的载荷角。

2.3 齿轮啮合热应力及热弹耦合应力

2.3.1 齿轮啮合热应力

物体由于温度的升高将产生热膨胀，同时由于外载荷或外部约束的限制将产生热应力。如长度为的钢棒，当均匀受热，温度由0升高到时，钢棒沿长度方向的线膨胀量为Δ=(−0)。若钢棒两端刚性固定且无法产生弯曲变形时，相当于钢棒受热后受到一轴向压力，使长度为Δ的钢棒产生轴向压缩变形Δ，钢棒内将出现压缩应力。若压缩变形全都是弹性变形，则有

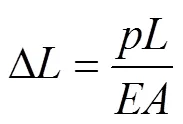
式中：为材料的弹性模量；为材料的截面积；为钢棒的压缩刚度。

由以上分析可知：物体在完全约束状态下的受热膨胀，其产生的热应力为物体热膨胀方向的刚度与物体自由状态下热膨胀量的乘积。对于无齿侧间隙的啮合齿轮对，在本体温度的作用下，啮合点的热应力t为

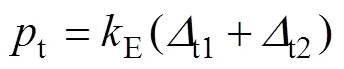
式中：E为齿轮的啮合弹性刚度；t1和t2为主、从动轮的热膨胀量。

2.3.2 齿轮啮合热弹耦合应力

齿轮在啮合的过程中，热应力和弹性应力互相作用并相互耦合，产生热弹耦合应力。热弹耦合应力的计算非常复杂，本文引入修正系数te对热应力进行修正，得到的热弹耦合应力计算公式如下：

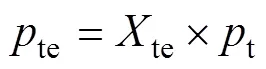
2.4 时变啮合合热刚度

2.4.1 热弹耦合变形

齿轮在外载荷与热应力、热弹耦合应力产生的附加载荷的共同作用下产生大的弹性变形，同时由于温度的升高齿廓将产生热膨胀，且弹性变形的方向与热膨胀的方向相反，因此，齿轮热弹耦合变形量为弹性变形量与热膨胀量的差值。即tei=ei−ti。其中轮齿在外载荷与热附加载荷、热弹耦合附加载荷作用下的弹性变形ei的计算公式为

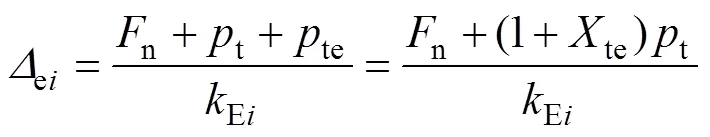
式中：Ei为齿轮的单齿弹性刚度；=1，2，分别表示主、从动轮。

2.4.2 齿轮热刚度

根据热刚度的定义及前述分析，主、从动轮的单齿热刚度Ti以及齿轮对的啮合热刚度T的计算公式分别如下：

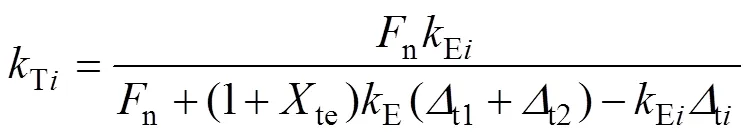
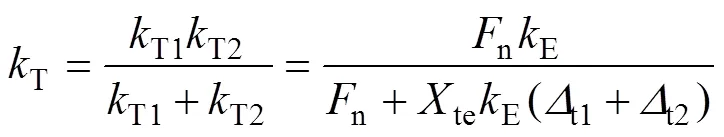
值得注意的是：当热应力修正系数te=0时，T=E。但在实际工况中，热弹耦合应力是确实存在的，即te＞0，因此，热弹耦合热刚度小于弹性刚度，这也与材料加热变软刚度降低的常识相符合。te的确定相对复杂，本文将通过有限元的方法，分别计算齿轮啮合点法向的弹性变形量和热弹耦合变形量，得到弹性变形与热弹耦合变形的比例关系再反求热弹耦合应力修正系数te。

由式(11)可知：当(1+te)E(t1−t2)−Eiti=0时，热刚度与弹性刚度相等。由刚度的串联特性可知：E总是小于Ei，尤其在齿根部分Ei远大于E。因此，上式在靠近过齿根部分存在零点，且由于单齿刚度的连续单调性，零点是唯一的。由此可知，单齿热刚度与弹性刚度沿啮合线的分布曲线存在唯一交点，在交点的一侧热刚度大于弹性刚度，在另一侧热刚度小于弹性刚度。

将式(12)的左右两端同时除以齿轮的啮合弹性刚度E，化简整理得

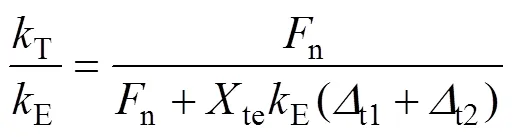
式中：n和te为定值；t1，t2和E沿啮合线非线性分布，因此，热刚度与弹性刚度沿啮合线也为非线性关系。由于弹性刚度E在啮入、啮出点取最小值，在节点处取最大值，所以，相对于弹性刚度，热刚度在啮入、啮出端的下降较少，在节点附近的下降量最大，啮合热刚度沿啮合线的分布更加平缓。

根据刚度与柔度的关系，将式(12)取倒数得到啮合齿轮对在啮合点总的热柔度T。齿轮啮合点总热柔度与弹性总柔度的差值为

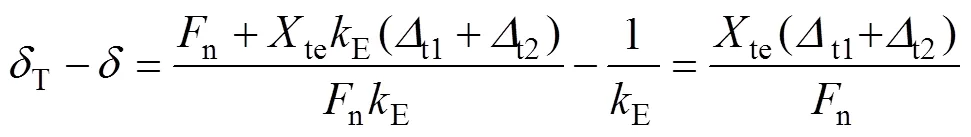
由式(14)可知：齿轮啮合点总柔度的差值仅与齿轮外载荷n、热应力修正系数te及啮合点主、从动轮热膨胀之和(t1+t2)有关。根据柔度的定义，式(14)可简化为

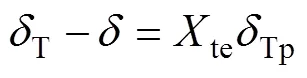
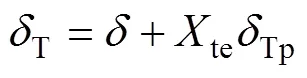
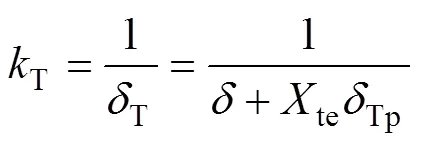
由式(16)和(17)可知：齿轮在热弹耦合作用下啮合点总的热柔度T为啮合点弹性柔度()与修正的热膨胀柔度(teTp)之和。齿轮在热弹耦合作用下的啮合热刚度为齿轮的啮合弹性刚度与修正的热膨胀刚度的串联。同理可得热弹耦合作用下的齿轮单齿热刚度：

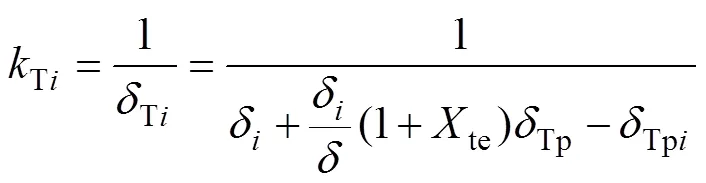
式中：δ为单齿弹性柔度；Tpi为单齿热膨胀柔度；=1，2，分别表示主、从动轮。

2.5 计算实例

传动齿轮副的基本参数如表1所示。根据以上分析，利用MATLAB软件编写计算程序，得到热弹耦合条件下齿轮热刚沿啮合线的分布，如图2所示。

表1 齿轮传动系统的相关参数

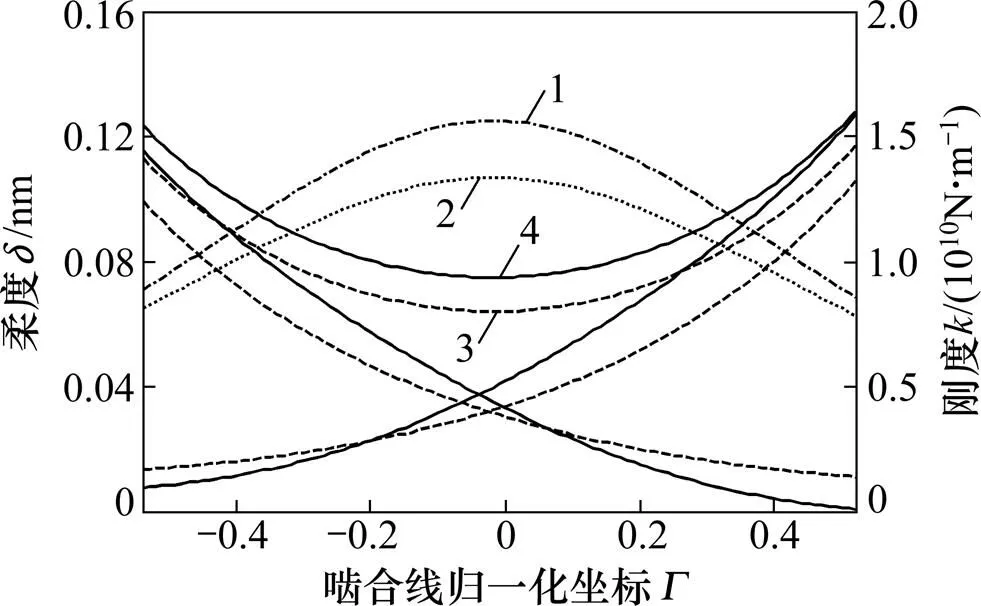
1—弹性刚度；2—热刚度；3—弹性柔度；4—热柔度。

3 齿轮热刚度的有限元法

3.1 热弹耦合变形的有限元法

有限元热弹耦合的方法分为直接耦合和间接耦合。本文采用间接耦合的方式，先利用APDL语言建立啮合齿轮对的三维实体模型，设定齿轮各个表面的对流换热系数，并给定啮合面上的摩擦热流密度，求解啮合齿轮对的稳态温度场。在进行结构分析时，再将得到的稳态温度场以载荷的方式施加到模型上，进行间接的热弹耦合接触分析。

对于热弹耦合接触分析，在啮合面处建立接触对。在研究主动轮的热弹耦合变形时，为消除刚体位移的影响，设定主动轮内孔表面上所有节点的三向位移均为0 mm，同时设定单齿两齿侧表面的周向位移为 0 mm。约束从动轮内孔表面的轴向和径向位移，同时在周向施加等效载荷。研究从动轮的热弹耦合变形时，设定从动轮内孔表面上所有节点的三向位移均为 0 mm，同时设定单齿两齿侧表面的周向位移为0 mm。约束主动轮内孔表面的轴向和径向位移，同时在周向施加等效载荷。

热弹耦合状态下，主动轮的变形云图如图3所示。由图3可知：由于变形的叠加效果，主动轮热弹耦合变形量在齿顶处最大，但最大位移点并非齿轮对的实际啮合点。实际啮合点需要通过热弹耦合的应力状态来判断。

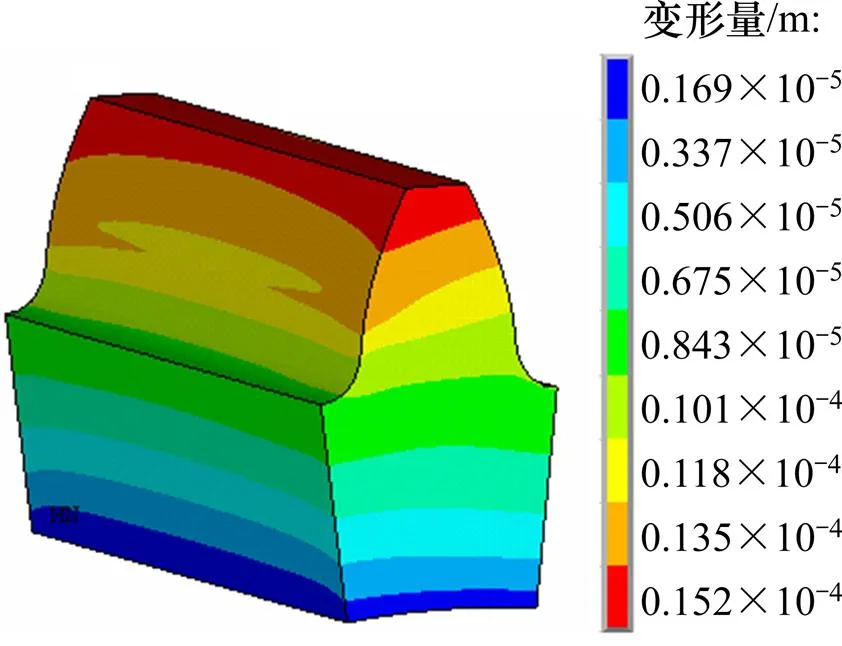
图3 主动轮热弹耦合变形

图4所示为主动轮啮合面热弹耦合作用下的米塞斯应力及接触面的接触应力云图。由图4可知：在啮合面上接触应力与米塞斯应力均在相同位置出现峰值，可以认为啮合面上应力最大位置即为实际啮合位置。提取最大应力点处的热弹耦合变形量即为实际接触点的热弹耦合变形量。

图5所示为啮合齿轮对的平面模型。坐标系为有限元的全局坐标系，111和222分别为主、从动轮齿廓建模标准坐标系。在实际的啮合过程中，随着啮合角度的变化，主、从动轮齿廓建模标准坐标系需要绕各自的轴转动角度1和2形成新的啮合坐标系111和222。对于不同的啮合位置，有限元输出的节点坐标及节点变形量均为全局坐标系下的数据。因此，需要将主、从动轮的节点数据从全局坐标系下转换到各自的啮合坐标系下。

设主、从动轮啮合点在全局坐标系下的坐标为(x，y，z)，点主、从动轮的热弹耦合变形量分别为(Δx1，Δy1，Δz1)和(Δx2，Δy2，Δz2)，经过坐标变换后，点在主、从动轮的啮合坐标系下的坐标及热弹耦合变形量分别为(′1，′1，′1)，(′2，′2，′2)，(Δ′1，Δ′1，Δ′1)和(Δ′2，Δ′2，Δ′2)。变换前后的坐标关系式如下。

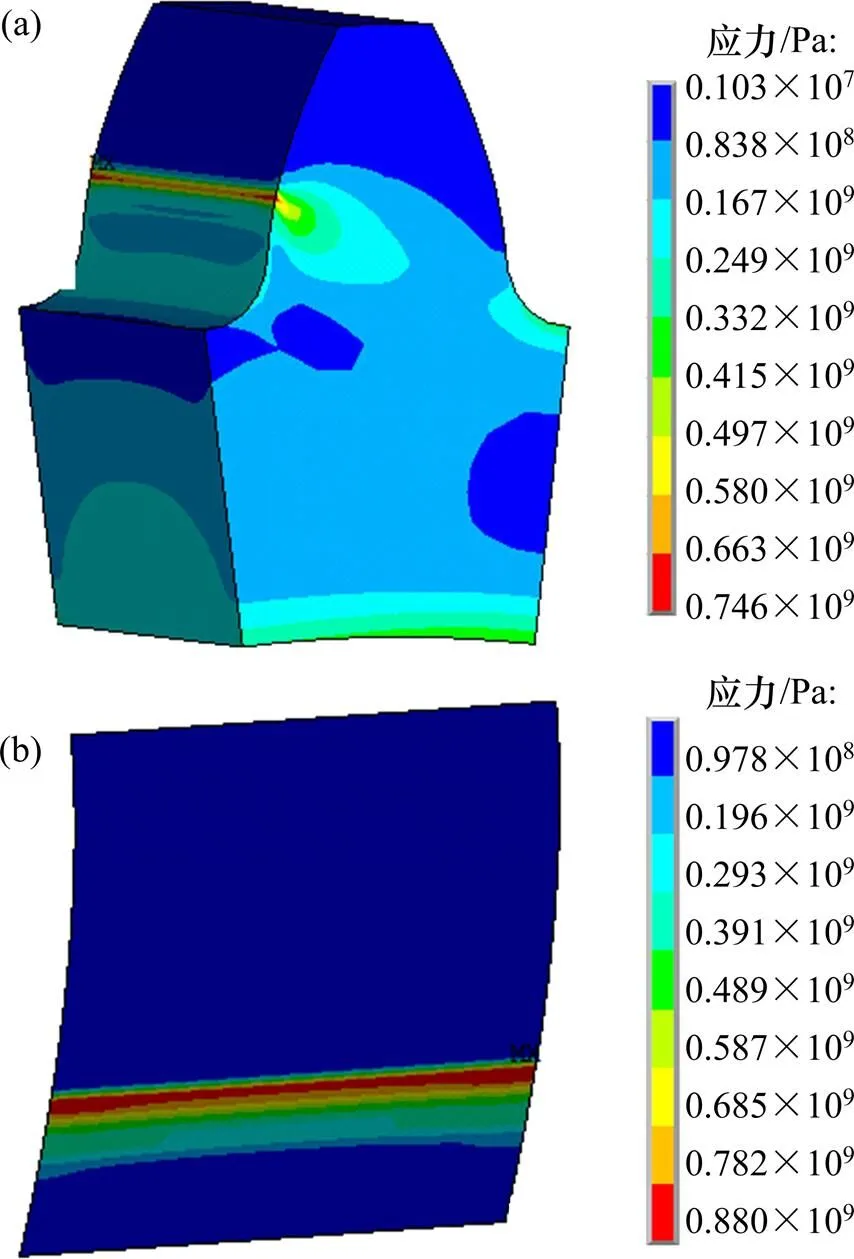
(a) 热弹耦合米塞斯应力；(b) 热弹耦合接触应力

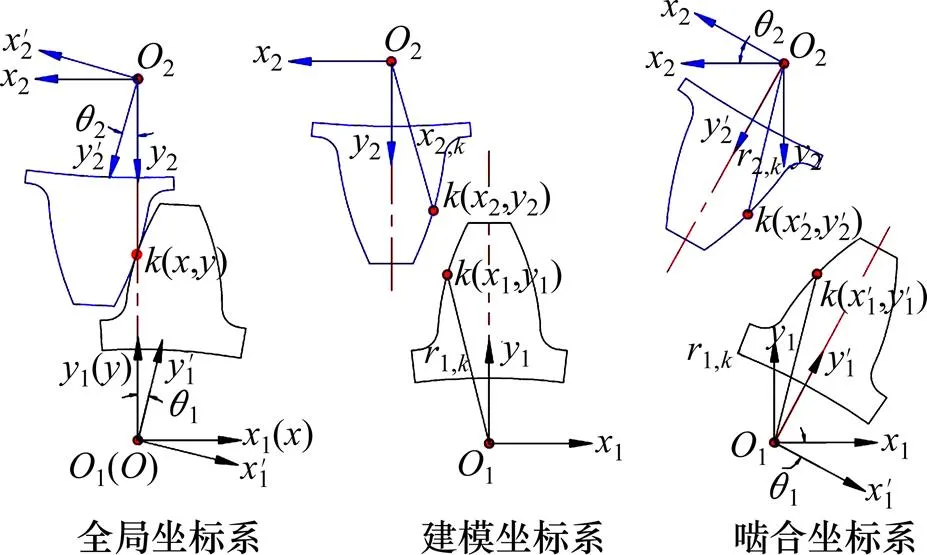
图5 啮合齿轮对平面模型

对于主动轮，有

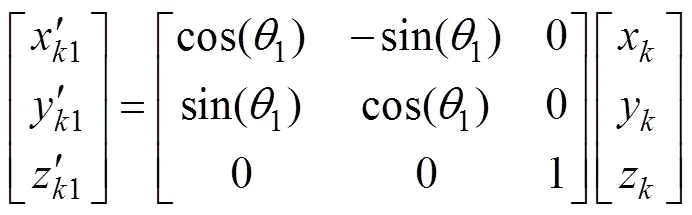
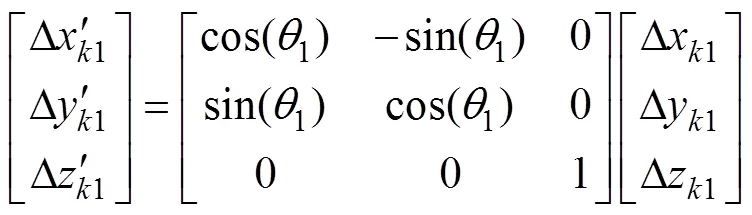
对于从动轮，有

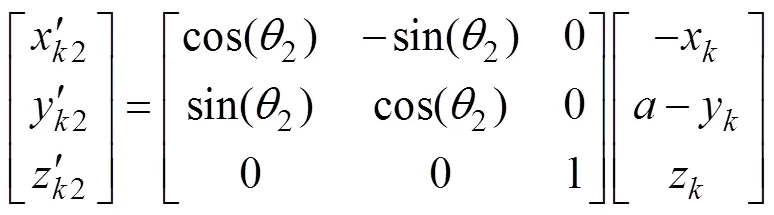
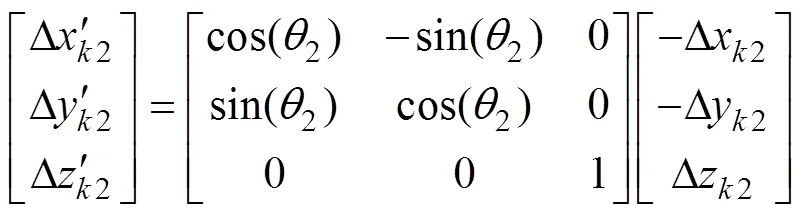
式中：1和2分别为齿轮啮合过程中主、从动轮标准建模坐标系绕轴转过的角度；为啮合齿轮对的中心距。

经过变换后得到啮合点热弹耦合状态下沿坐标轴和方向的2个耦合变形分量。根据热刚度的定义，需要计算啮合点法向的耦合变形量。因此，需要将和方向的2个耦合变形分量投影到啮合点的法向方向，其计算过程如下：

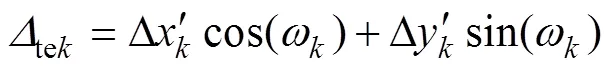
式中：Δ', Δ'分别表示经过坐标变换后的热弹耦合变形分量；tek为啮合点沿啮合线方向的热弹耦合变形量。

经过变换及投影后主动轮啮合面的弹性变形及热弹耦合变形量如图6所示。

由图6可知：由于变形的叠加效果，变形量从齿根到齿顶处逐渐增大。但在实际啮合点处由于接触变形、热弹耦合应力等的共同作用，变形量出现峰值，该峰值即为啮合点的热弹耦合变形量。在齿根端，热弹耦合的变形量比弹性变形量小；在齿顶端，热弹耦合的变形量比弹性变形量大。齿宽方向由于边缘效应，弹性变形量在齿宽边缘大，齿宽中部小。但齿宽中部热弹耦合变形量比边缘的大，其主要原因是齿宽中部温度高，热膨胀量大，热弹耦合应力大。

综上所述，热弹耦合变形的有限元法是通过间接耦合方法得到啮合面的总变形量，即通过啮合面的应力状态找到实际啮合点的节点坐标，再通过坐标变换和投影得到啮合点的法向热弹耦合变形量。

3.2 基于有限元的齿轮热刚度

将上文计算得到的啮合点的热弹耦合变形量，代入式(1)可得到齿轮啮合点的热刚度。在整个啮合线上取若干离散的啮合点，分别计算出各离散啮合点的热刚度，再利用曲线拟合的方法便可得到单齿热刚度沿啮合线的分布曲线，即单齿刚度曲线。齿轮对的啮合热刚度相当于2个单齿热刚度的串联，公式如下：

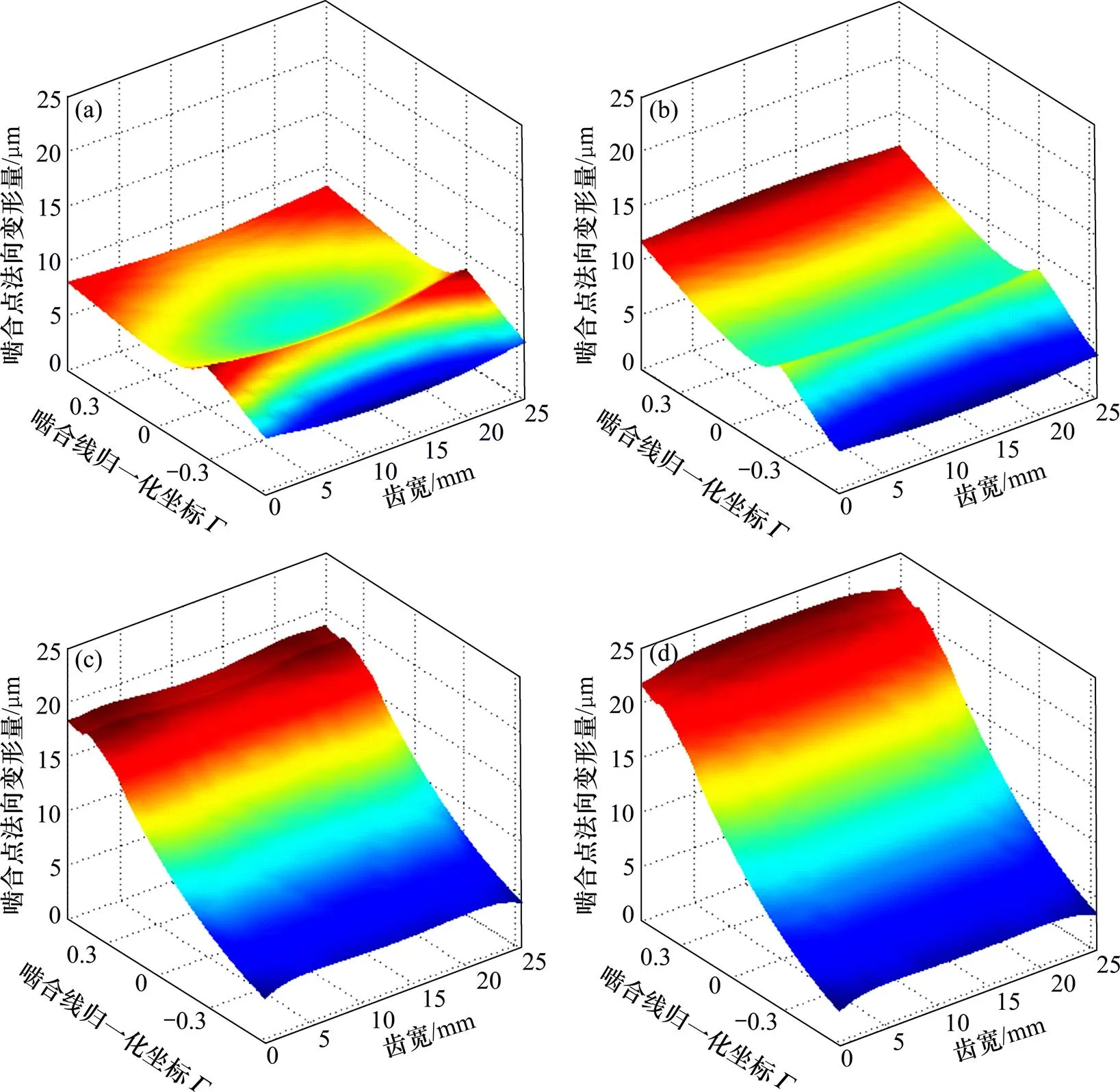
(a) 齿根端啮合面弹性变形量；(b) 齿根端啮合面热弹耦合变形量；(c) 齿顶端啮合面弹性变形量；(d) 齿顶端啮合面热弹耦合变形量

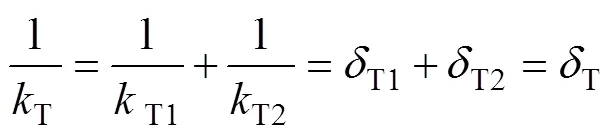
式中：T为啮合齿轮对的啮合热刚度；T为啮合齿轮对的热柔度；T1和T2分别为主、从动轮的单齿热刚度；T1和T2分别为主、从动轮的热柔度。

针对本文研究对象，通过多个离散啮合点的分析及对数据点的曲线拟合得到齿轮对的啮合热刚度沿啮合线的分布曲线，如图7所示。

由图7可知：在整个啮合区域啮合齿轮对的热刚度均小于弹性刚度。但单齿热刚度沿啮合线的分布曲线与弹性刚度分布曲线存在唯一交点，交点位于各自齿轮齿廓的齿根附近。在交点的齿根侧，热刚度比弹性刚度大，齿顶侧热刚度比弹性刚度小。

对比图2和图7可知：2种方法的计算结果在柔度和刚度的变化趋势上完全一致，仅在具体的数值上存在细微差别，进一步证明了热刚度计算方法的准确性。

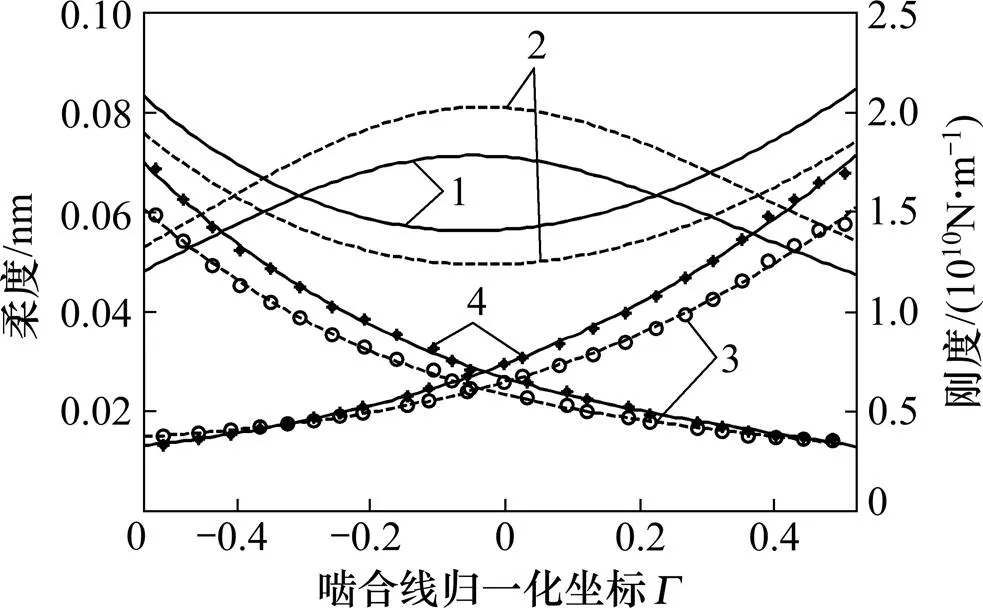
1—有限元数据拟合热柔度、刚度曲线；2—有限元数据拟合弹性柔度、刚度曲线；3—有限元单齿弹性柔度数据及拟合曲线；4—有限元单齿热柔度数据及拟合曲线。

4 结论

1) 对于啮合刚度，在整个啮合区域，热刚度小于弹性刚度，且热刚度与弹性刚度呈非线性关系，热刚度与弹刚度在啮入、啮出端差距小，在节点附近差距最大。

2) 对于单齿刚度，热刚度和弹性刚度曲线在靠近齿根部位存在唯一交点，热刚度在交点的齿根侧大于弹性刚度，在交点的齿顶侧小于弹性刚度。

3)齿轮在热弹耦合作用下啮合点总的热柔度T为啮合点弹性柔度与修正的热膨胀柔度之和；热刚度为齿轮对的弹性刚度与修正的热膨胀刚度的串联。

[1] FERNANDEZ DEL RINCON A, VIADERO F, IGLESIAS M, et al. A model for the study of meshing stiffness in spur gear transmissions[J]. Mechanism and Machine Theory, 2013, 61: 30−58.

[2] CHEN Zaigang, SHAO Yimin. Mesh stiffness of an internal spur gear pair with ring gear rim deformation[J]. Mechanism and Machine Theory, 2013, 69: 1−12.

[3] PEDERSEN N L, JØRGENSEN M F. On gear tooth stiffness evaluation[J]. Computers and Structures, 2014, 135: 109−117.

[4] 刘志峰, 张志民, 张敬莹, 等. 基于多项式的等高齿锥齿轮时变啮合刚度建模[J]. 吉林大学学报(工学版), 2013, 43(4): 939−944. LIU Zhifeng, ZHANG Zhimin, ZHANG Jinying, et, al. Modelling of high-spiral bevel gear mesh stiffness based on polynomial[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 939−944.

[5] HEDLUND J, LEHTOVAARA A. A parameterized numerical model for the evaluation of gear mesh stiffness variation of a helical gear pair[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2008, 222(7): 1321−1327.

[6] 唐进元, 蒲太平. 基于有限元法的螺旋锥齿轮啮合刚度计算[J]. 机械工程学报, 2011, 47(11): 23−29. TANG Jinyuan, PU Taiping. Spiral bevel gear meshing stiffness calculations based on the finite element method[J]. Journal of Mechanical Engineering, 2011, 47(11): 23−29.

[7] RAGHUWANSHI N K, PAREY A. Experimental measurement of gear mesh stiffness of cracked spur gear by strain gauge technique[J]. Measurement, 2016, 86: 266−275.

[8] MUNRO R G, PALMER D, MORRISH L. An experimental method to measure gear tooth stiffness throughout and beyond the path of contact[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2001, 215(7): 793−803.

[9] PANDYA Y, PAREY A. Experimental investigation of spur gear tooth mesh stiffness in the presence of crack using photoelasticity technique[J]. Engineering Failure Analysis, 2013(34): 488−500.

[10] SHI Jialian, MA Xiaogang, XU Changliang, et al. Meshing stiffness analysis of gear using the Ishikawa method[J]. Applied Mechanics and Materials, 2013, 401/402/403: 203−206.

[11] LIANG Xihui, ZUO M J, PATEL T H. Evaluating the time-varying mesh stiffness of a planetary gear set using the potential energy method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(3): 535−547.

[12] 李亚鹏, 孙伟, 魏静, 等. 齿轮时变啮合刚度改进计算方法[J]. 机械传动, 2010, 34(5): 22−26. LI Yapeng, SUN Wei, WEI Jing, et al. Study on the improved algorithm of the time-varying meshing stiffness of gear[J]. Journal of Mechanical Transmission, 2010, 34(5): 22−26.

[13] PANDYA Y, PAREY A. Simulation of crack propagation in spur gear tooth for different gear parameter and its influence on mesh stiffness[J]. Engineering Failure Analysis, 2013, 30: 124−137.

[14] LIANG Xihui, ZUO M J, PANDEY M. Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set[J]. Mechanism and Machine Theory, 2014, 76: 20−38.

[15] HU Yumei, XUE Desheng, PI Yangjun. Effect of friction coefficient on the stiffness excitation of gear[J]. Applied Mechanics and Materials, 2011, 86: 713−716.

[16] 陈立锋, 吴晓铃, 罗善明. 误差对轮齿刚度的影响分析[J]. 农业机械学报, 2008, 39(3): 137−139. CHEN Lifeng, WU Xiaoling, LUO Shanming. Analysis of influences of the error on the gear stiffness[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(3): 137−139.

[17] CHEN Zaigang, SHAO Yimin. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013, 62: 63−74.

[18] 冯松, 毛军红, 谢友柏. 齿面磨损对齿轮啮合刚度影响的计算与分析[J]. 机械工程学报, 2015, 51(15): 27−31. FENG Song, MAO Junhong, XIE Youbai. Analysis and calculation of gear mesh stiffness with tooth wear[J]. Journal of Mechanical Engineering, 2015, 51(15): 27−31.

[19] 薛建华, 李威, 李启超. 基于时变刚度的齿轮系统动载荷及热弹流润滑分析[J]. 中南大学学报(自然科学版), 2014, 45(8): 2603−2609.XUE Jianhua, LI Wei, LI Qichao. Dynamic load and thermal elastohydrodynamic lubrication of gear system based on time-varying stiffness[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2603−2609.

[20] 李桂华. 复杂规则曲面机械零件的热变形理论及应用研究[D]. 合肥: 合肥工业大学机械与汽车工程学院, 2006: 54−60. LI Guihua. Theoretical and applied research of thermal deformation of complicated machine components with regular camber[D]. Hefei: Hefei University of Technology. School of Mechanical and Automotive Engineering, 2006: 54−60.

(编辑 伍锦花)

Research on thermal stiffness of gear based on thermo-elastic coupling

LUO Biao1, 2, LI Wei1, LI Linsheng2

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;2. School of Mechanical Engineering, University of South China, Hengyang 421001, China)

To study the influence of temperature on gear stiffness, the concept of thermal stiffness of gear was proposed, and its calculation method was defined. The correction factor of thermal stresstewas proposed, and the calculation methods of the thermo-elastic coupling stress and deformation were obtained. The single tooth thermal stiffness and the meshing thermal stiffness of gear were calculated by finite element method and analytical method, respectively. The calculation results of the two methods were basically consistent. The results show that the thermal stiffness of gear under the condition of thermo-elastic coupling is a combination of elastic stiffness and modified thermal expansion stiffness. The meshing thermal stiffness of gear pair is decreased when compared with the meshing elastic stiffness. There is only one intersection point between the single tooth thermal stiffness and elastic stiffness distribution curves along the meshing line, and the intersection point is located near the root area. The thermal stiffness is greater than the elastic stiffness in the root side of the intersection point, and is less than the elastic stiffness on the tip side of the intersection point.

thermo-elastic coupling; thermal stiffness; gear; finite element method; analytical method

10.11817/j.issn.1672−7207.2017.12.010

TH132.4

A

1672−7207(2017)12−3209−07

2017−01−05；

2017−02−26

国家自然科学基金资助项目(51775036)(Project (51775036) supported by the National Natural Science Foundation of China)

李威，博士，教授，从事机械传动与控制、数字化设计与制造技术、机械设计模糊方法、虚拟样机技术和仿真技术等研究；E-mail：liwei@me.ustb.edu.cn