一种改进的运动模糊图像修复参数计算方法*
2018-01-27向怀坤白云海
向怀坤,白云海
(1. 深圳职业技术学院 汽车与交通学院,广东 深圳 518055;2. 辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
随着地面视频监控、高低空航拍摄影等应用的普及,特别是智能交通系统(Intelligent Transportation Systems,简称ITS)领域对视频图像应用需求的不断扩展,人们对图像质量的要求也越来越高.而图像模糊问题始终存在,特别是在拍摄对象处于相对运动状态时,因聚焦、曝光等原因很容易产生图像模糊,严重影响拍摄图像的成像质量.
在运动模糊图像的修复过程中,运动模糊参数的精确获得是关键影响要素.运动模糊参数主要包括:模糊方向和模糊长度.文献[1]和[2]对倒谱域进行了研究,通过把高斯差分作为倒频谱变换的输入参数,将模糊运动目标从图像中分离出来,但该方法在实际应用中有较大的局限性.文献[3]和[4]对退化图像的频谱特征进行了分析,并分别采用Lucy-Richardson和维纳滤波进行模糊图像复原;文献[5]分析了模糊图像频谱中亮暗条纹的成因,采用SOBEL算子进行一阶微分运算;文献[6]采用四邻近像素加权法得到了点扩展函数;文献[7]从理论上推导了图像模糊方向与亮暗条纹方向之间的关系,并采用Canny算子转抑制频谱中的亮十字.这些方法都对运动模糊参数的精确计算进行了探索,但是总体上计算过程较为复杂.
在前人研究的基础上,本文提出图像边界模糊以消除中心亮十字从而提升运动模糊方向的检测质量,通过对频谱图像进行垂直方向线积分获得局部极小均值来提升模糊长度的计算精度,最后以无人机实际航拍的模糊图像对所提出的改进方法进行了对比验证.
1 运动模糊的基本原理
在基于空中运载体的图像 f (x, y)获取过程中,由于载体(如航天器、飞机、低空无人飞行器等)本身与被摄目标之间存在相对移动,在曝光时间内会导致邻域像素沿运动方向叠加,掩盖了图像中许多有用的信息[8],从而产生图像的运动模糊.
如文献[9]所述,当搭载相机的高空平台以一定的速度v飞越地面被拍摄目标上空进行拍摄时,假设相机的焦距为 f′,相机距离拍摄场景的高度为H,在拍摄瞬间的一段曝光时间内,相机与被拍摄目标相对移动,对应的在影像上相邻像素之间重叠会产生一定距离的像移S,相机的曝光时间T可以从相机参数手册中获得,这样便可以通过公式(1)得出像移S.假设地面目标的实际位置为A,在影像中的对应位置为a,A’表示经过相对移动后A的位置,a’表示经过相对移动后a的位置,图1示意了像移过程.
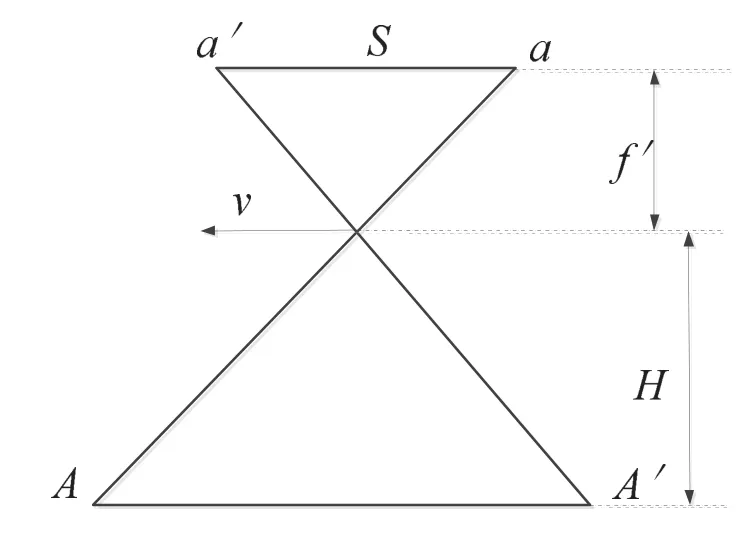
图1 像移过程示意图

像移 S是图像模糊的重要因素.根据文献[10]对信号与系统的关系描述,可以这样理解成像过程:原始拍摄图像f (x, y)相当于对系统的激励也就是输入信号,此信号只能取在规定范围内的离散数值;模糊图像相当于输出信号,即系统对激励的响应.假设h(x, y)是空间不变的、线性的过程,那么图像的退化过程在空间域及频域表示如下:
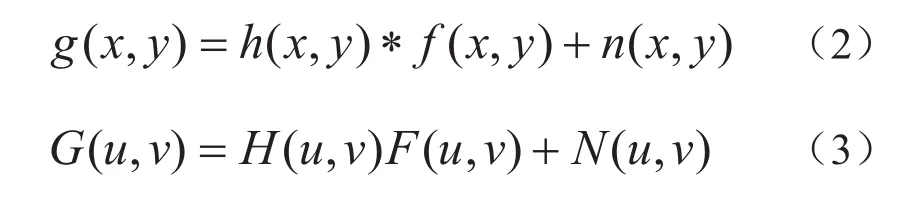
其中,x, y表示图像中每个像素的行列位置,g(x, y)表示退化后的模糊图像,h(x, y)表示点扩展函数(Point Spread Function,简称PSF),即退化函数,f (x, y)表示原始图像,“*”表示对f(x, y)和h(x, y)进行卷积运算,n (x, y)表示可加性噪声;G(u, v), H(u, v), N(u, v)分别表示式(2)中相应函数的频域表示,u, v分别表示二维频谱图像中的2个频率变量.在式(2)中假如不考虑噪声,那么可以改写为:
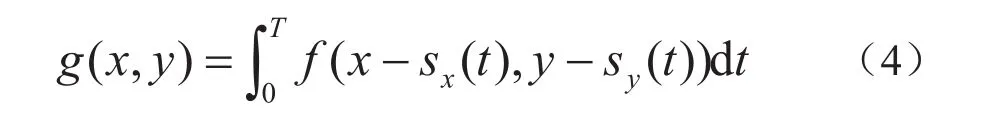
2 运动模糊参数求取的改进方法
2.1 运动模糊频域变换
在频率域中h(x, y)的傅里叶变换H(u, v)一般叫做光学传递函数(Optical Transfer Function,即OTF).在成像过程中OTF描述了调制度和横向相移之间的相对变化.PSF是光学传递函数的傅里叶反变换.对式(4)的傅里叶变换过程进行推导,以得出h(x, y)的变换结果OTF.M, N分别表示图像的行数和列数.
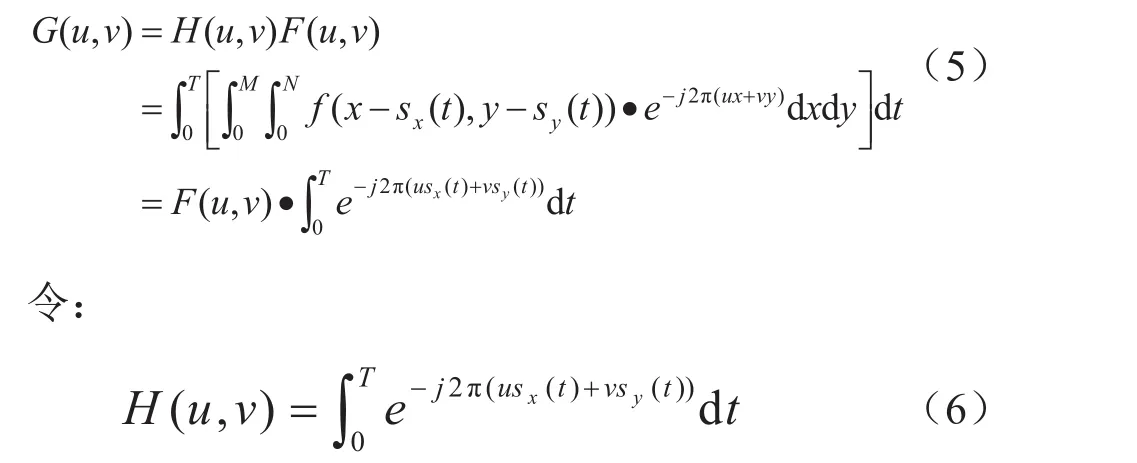
这样便得出h(x, y)的傅里叶变换.设在曝光时间T内,像移距离S分别在x, y轴上的投影长度为Sa和 Sb,那么就可以计算出像素点从曝光开始到 t时刻所移动的距离Sx(t)和Sy(t).
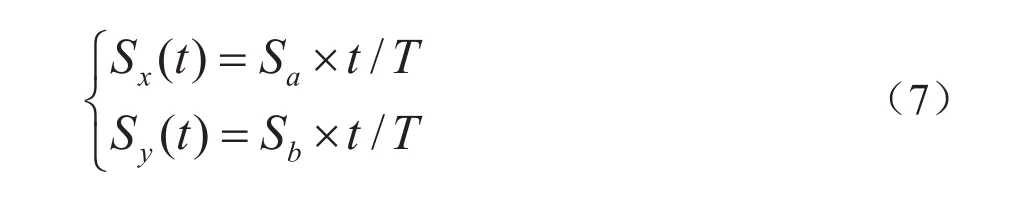
把式(7)代入到式(6)中,计算定积分得出:
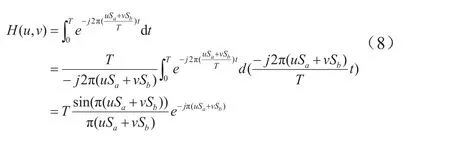
由于图像是以离散的数字阵列形式存储在计算机中,所以对式(8)的连续形式进行离散化,最终得到:
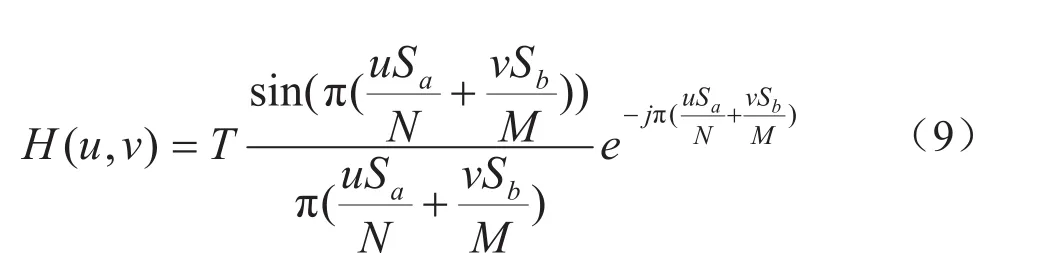
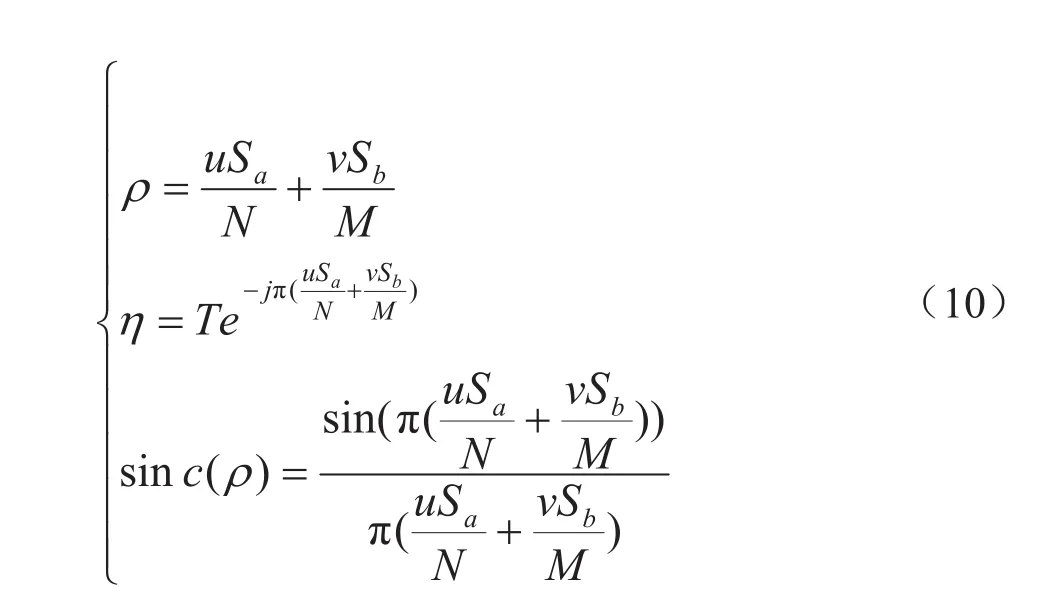
把式(10)代入式(9)进行简化得到:

对基于运动模糊的图像频谱来说,图像中心是一条亮带,在中心的两侧会出现等间距明暗相间的条纹,参数η相当于振幅,η的变化随着ρ的增大而减小,因此当噪声很小时在频谱图像上呈现出从中心到两端逐渐变暗的趋势.
2.2 消除频谱亮十字
图像在拍摄时相当于只是对信号一个周期的采样.在基于频域的运动模糊图像参数提取过程中,离散傅里叶变换假设一幅图像的频域模式是周期变化的,这样的假设导致在图像边界产生频谱骤降,截断了频谱的连续性.对图像经过离散傅里叶变换并居中处理之后会发现,频谱图像中心出现2条中心相互垂直的亮条纹,这种亮条纹又被称为频谱亮十字.
研究表明,频谱亮十字是造成运动模糊参数计算误差的重要影响因素[3-15].本研究提出的一种消除频谱亮十字的改进方法,与文献[7]不同的是,本文的改进方法中在Canny边缘检测之前使用了边界模糊来消除亮十字.通过多次实验,我们发现频谱在图像边界处被截断,频谱的不连续是导致中心亮十字产生的根本原因,为此采用高斯滤波对图像边界进行模糊,可使图像边界的高频部分被减弱.具体的方法如下:
1)将高斯低通滤波模板作用于整幅图像;
2)模糊后的图像与原始图像进行加权求和,新图像边界采用上一步的图像像素值,其余像素采用原始图像的像素.
图2显示了边界模糊前后和消除频谱亮十字前后二值图像之间的对比.

图2 消除频谱亮十字
2.3 运动模糊方向计算的改进
通过运动模糊函数h(x, y)分析,在知道模糊方向角的情况下可以求出模糊长度.下面首先从频谱对模糊方向角α入手进行分析.在式(10)中,参数ρ对频谱的角度有决定作用,当ρ=0,uSa/ N + vSb/ M = 0,即直线的表达式,u和v相当于直线公式中的自变量和因变量.假设这条直线的倾斜角为β,那么它的斜率可以表示为:
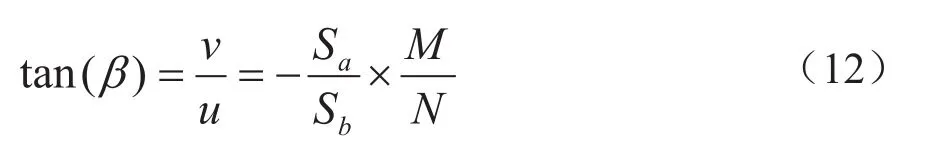
在式(7)中提到Sa和Sb别是像移S在坐标轴上的投影长度,因此模糊长度的斜率就是:

这里依然使用α表示运动模糊方向.结合以上式(12)和式(13)可以得到频谱条纹倾斜角和模糊长度倾斜角之间的关系:
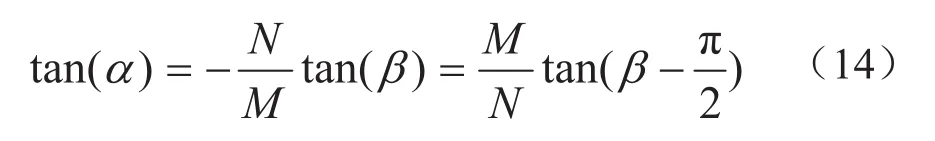
2.4 运动模糊长度计算的改进
将图像由空间域通过傅里叶变换到频域之后,原图像中的重要细节部分主要集中在频谱图像的中心也就是0频部分.虽然图像旋转之后会丢失一部分信息,但是重要的细节仍然会在频谱中保留.通过频谱旋转可以将二维问题转换成一维进行分析,简化对问题的分析难度.基于运动模糊方向角α把频谱图像沿着反方向旋转,旋转角度为-α.旋转后的结果相当于原图像沿着水平方向进行了运动模糊,此时频谱图像的条纹方向处于垂直状态,因此式(11)可以简化为:它的傅里叶变换及离散化表示为:

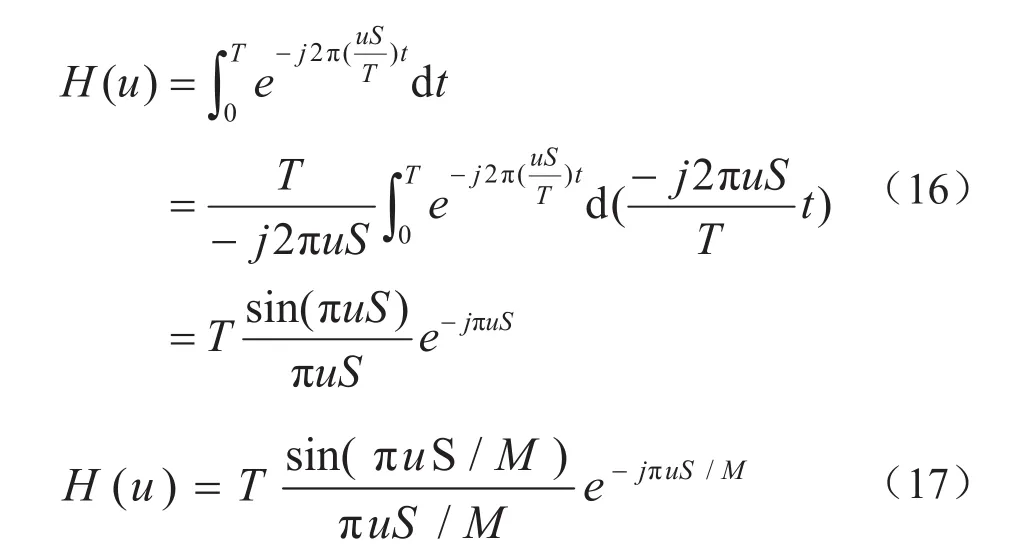
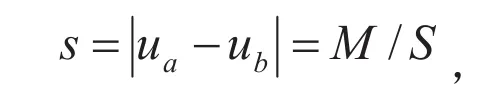

3 实验与分析
3.1 基于仿真的运动模糊方向检测
采用MATLAB中的peppers图像,并截取256×256大小进行消除频谱亮十字的改进方法仿真实验,其中同样使用Canny算子进行边缘检测.
实验设定模糊长度范围为1~30个像素,模糊方向为0°~ 180°.针对每个设定的模糊长度进行0°~ 180°的模糊方向检测,最终结果与设定的模糊方向进行比较获得角度误差;每个模糊长度对应181个角度值,生成5430个角度检测结果中与设定值进行比较,并与加春燕[6]的方法检测结果进行对比.表 1列出了检测结果的对比情况(长度用像素个数表示).
由表1可知,当模糊长度较小时,模糊方向的检测很不明感,尤其是模糊长度为1~7个像素的时候.相比之下,本文的检测结果较文献[7]的方法稍好.另外,消除频谱亮十字之后,模糊方向的检测误差有所下降,说明亮十字的存在对基于频谱的模糊方向的检测有一定的影响,同时通过实验数据说明本文通过边界模糊对消除频谱亮十字来提高模糊方向的检测精度起到了作用.
3.2 基于仿真的运动模糊长度检测
模糊方向的作用在于对频谱按照模糊方向的大小进行反方向旋转,最终是频谱条纹呈竖直方向,因此模糊方向的精确检测对模糊长度的估计起着确定性作用.其关键的一步就是如何获取极小值,文献[14]通过频谱分块的方法反向旋转频谱之后同样对其沿垂直方向进行积分,找到中心两边的两个极小值点,按照公式(18)计算模糊长度.文献[15]采用微分自相关法对模糊长度的提取与频谱分块法如出一辙,区别在于频谱分块法只用了频谱的四分之一.文献[7]采用MATLAB中的取局部极小值函数imreginalmin计算两个极小值点之间的距离,上述这些方法都是寻找中心点2侧的两个极小值.
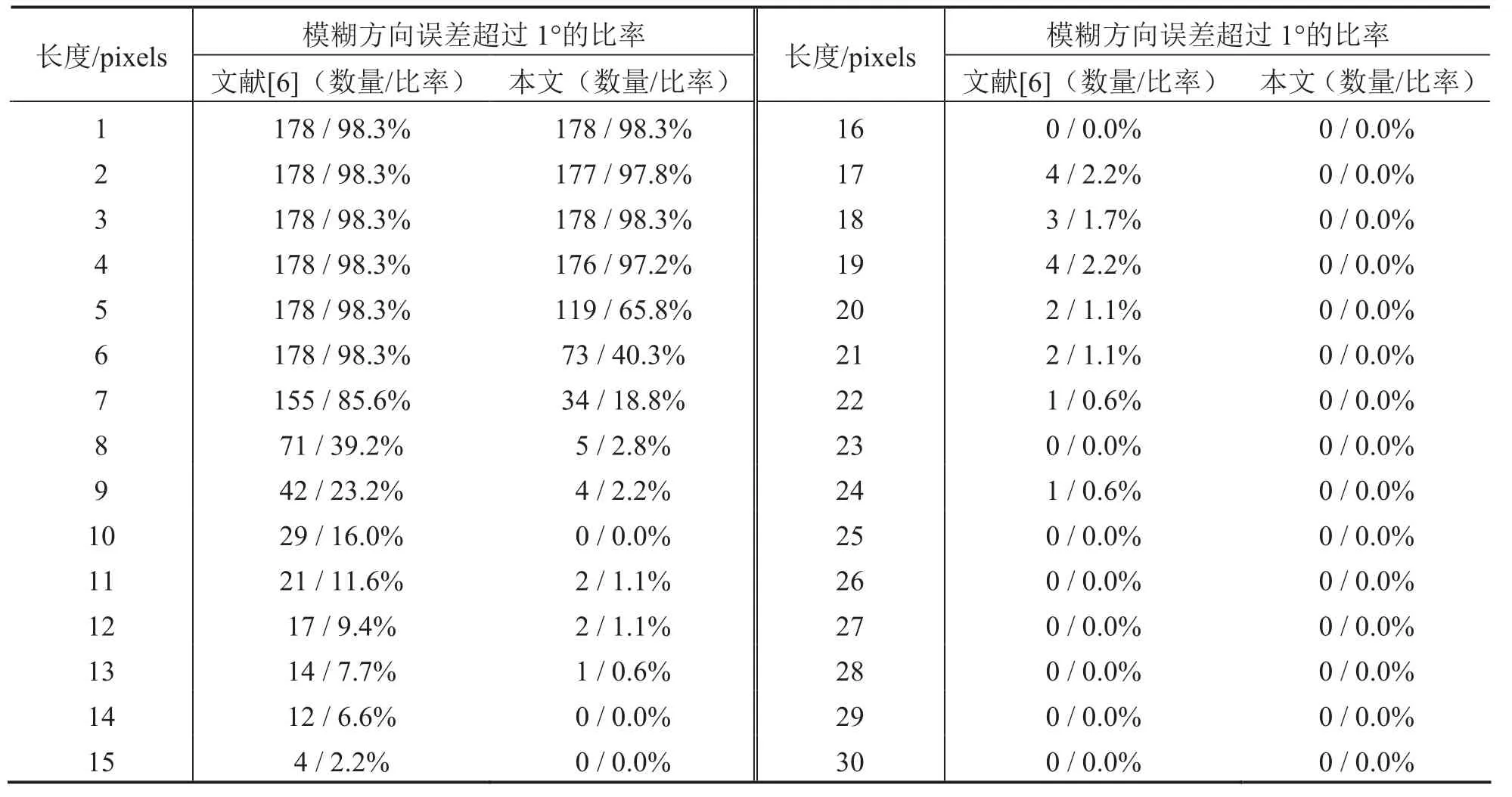
表1 模糊方向误差大于1°占模糊方向数的比例
本文提出的一种求取运动模糊长度的改进方法.该方法通过从积分曲线的中心开始向2边寻找,根据极小值定理可知,在一个局部范围内如果所有的值都比当前值大,那么就认为这个值在该区域内是极小值,通过相邻值之间相比较确定极小值,依次判断直到找到所有的极小值,考虑到误差的影响,只对中心值两侧的2个极小值差分做平均.利用Matlab以模糊长度为10个像素,模糊角度为 45°,对仿真运动模糊图像进行方向检测、频谱旋转、垂直积分,最后获得的模糊长度是9.9417,与设定值相差大约0.06,说明结果非常的接近.
3.3 基于无人机航拍模糊图像的处理
为了验证改进的运动模糊方向与运动模糊长度这两个运动模糊图像修复的关键参数的检测方法,本文采用六旋翼工业级无人机搭载高清摄像机获取视频图像数据.拍摄地点位于深圳市某主要干道的道路交叉口上空170 m.由于拍摄过程中无人机处于高速飞行状态,导致拍摄的视频图像产生了运动模糊.在室内的方法验证过程中,选择了视频图像中的部分区域进行运动模糊参数提取与模糊图像修复处理.其中图 3(a)为原始图像,图 3(b)为基于文献[7,12,13]的参数检测方法得到的图像修复图,图 3(c)为采用本文的参数检测方法得到的图像修复图.
由图 3可知,采用文献[7,12,13]获取的模糊方向和模糊长度对模糊图像修复后,振铃效应依然很明显,由于其采用了基于Canny算子的边缘检测方法对频谱亮十字进行抑制,经过维纳滤波复原后,图像中车辆和道路的周围出现了振铃,且车辆周围的振铃效应比较严重.本文通过采用边界模糊消除频谱亮十字的改进方法提高了运动模糊参数的检测精度,实验结果明显优于前者,从主观的角度去看边界模糊后的维纳滤波修复结果也更接近真实情况.

图3 无人机运动模糊图像修复对比图
4 结 论
在分析了运动模糊图像生成原理的基础上,提出图像修复过程中2个关键模糊参数检测的改进方法,通过实测无人机模糊图像对该方法进行了实验分析.研究结果表明:
1)在复原过程中模糊长度过小时无法进行检测甚至错误检测结果占绝大多数,当模糊长度设置在 10~30个像素时发现检测结果的质量有明显提高.
2)通过边界模糊后检测结果优于没有进行边界模糊的情况.并且边界模糊对图像复原质量有一定的改善作用.将检测方法应用于实际航拍图像得到了较好的恢复效果.
本文方法恢复图像中物体的边缘有轻微锐化,并且由于噪声的干扰,恢复的航拍图像存在有类似椒盐噪声的干扰,后续将进行进一步重点研究.
[1] Park J, Min K, Chang S, et al. Estimation of motion blur parameters using cepstrum analysis[C]/2011 IEEE 15th International Symposium. Singapore:Consumer Electronics (ISCE), 2011:406-409.
[2] Rom R. On the cepstrum of two-dimensional functions(Corresp.)[J]. IEEE Transactions on Information Theory, 1975,21(2):214-217.
[3] 王秋云,王轶群.基于Lucy-Richardson算法的运动模糊图像复原研究[J].自动化与仪器仪表,2013(2):13-14.
[4] 韩礼,张力军,蔡洪,等.基于维纳滤波的运动模糊星图复原仿真分析[J].光学技术,2014(4):316-320.
[5] 贤光,颜昌翔,张新洁,等.运动模糊图像点扩散函数的频谱估计法[J].液晶与显示,2014,29(5):751-755.
[6] 计岑.一种亚像素级的运动模糊点扩散函数的估计方法[J].广播电视信息,2015(5):73-75.
[7] 加春燕,崔丽.基于频谱边缘检测和Radon变换估计运动模糊图像的方向[J].图学学报,2016,37(3):434-438.
[8] 谢伟,秦前清.基于倒频谱的运动模糊图像PSF参数估计[J].武汉大学学报(信息科学版),2008,33(2):128-131.
[9] 谢伟.多帧影像超分辨率复原重建关键技术研究[M].武汉:武汉大学出版社,2014:50-148.
[10] 陈生潭,郭宝龙,李学武,等.信号与系统[M].西安:西安电子科技大学出版社,2014.
[11] Zhao Z H, Zhang L N, Liu X P, et al. Algorithm for the Removing Uniformed Motion Blur[J]. Computer Aided Drawing Design and Manufacturing (English), 2014(4):20-25.
[12] 陈至坤,韩斌,王福斌,等.运动模糊图像模糊参数辨识与逐行法恢复[J].科学技术与工程,2016(5):177-181.
[13] 加春燕.运动模糊图像运动长度的频谱估计法[J].北京工业职业技术学院学报,2015,14(1):51-54.
[14] 王琳,师雪艳,张少辉,等.基于Radon变换的遥感图像运动模糊参数精确估计[J].计算机应用研究,2015,32(12):3798-3800.
[15] 赵环旭.基于Radon变换的改进型运动模糊图像恢复[D].兰州:兰州交通大学,2014:13-51.
