基于模型构建与应用能力培养的离散数学教学研究
2018-01-27张赛男张婷婷刘艳云蒋园园
张赛男,张婷婷,刘艳云,蒋园园
(中国人民解放军陆军工程大学指挥信息系统学院,江苏南京210007)
离散数学是信息技术相关学科领域最重要的基础课程之一。文章提出结合探究式教学模式,在教学过程中培养学生离散结构模型的构建能力及利用构建的模型解决实际问题的应用能力。
离散数学;教学目标;探究式教学模式;离散结构模型构建;应用能力
0 引言
离散数学隶属自然科学类别,它的主要研究对象为离散结构及其相互间的关系,该课程集成了研究离散对象性质及其结构的若干数学专题。专题涉及集合论、逻辑学、数论、图论、代数系统等重要数学分支[1]。离散数学在信息技术相关学科领域,特别是在计算机科学与技术领域,得到了广泛的应用。
离散数学每个模块概念多、内容散、模块之间知识点联系少,理论、原理及证明具有极强的理论性和高度的抽象性。在教学过程中,教师只重视概念、定义和定理的证明以及理论知识的完整性,会使学生错误地认为这是一门纯理论课或者是一门数学课,学生会感觉学习这门课程没有任何用处。如何让学生感觉离散数学有用,如何能够把抽象的定理证明转化为解决实际问题的手段,这就需要将教学的重点放在基本的概念、理论和方法的应用上。
1 离散数学是计算机学科的理论基础
离散数学课程内容由计算机科学与工程实践中所需的数学理论和方法构成,具有重要的应用背景,是数字逻辑电路、数据结构、数据库原理、计算机网络等专业课程的基础,这些专业课程的基本概念、基本方法和基本原理都和离散数学密不可分。例如逻辑电路的设计需要逻辑学的支撑;集成电路的布线和网络线路的铺设过程中如何最优最快需要图论模块的支撑,密码学则需要代数知识的支撑,数据库的管理则需要组合论的支撑,等等。离散数学和这些课程有千丝万缕的联系,并且在计算机学科发展过程中起着重要作用,如图1所示[2]。
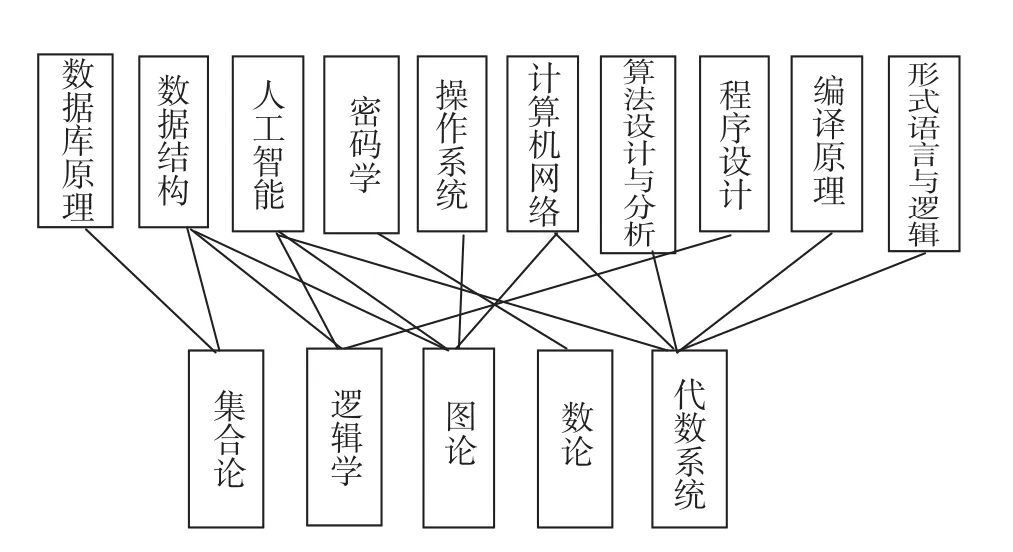
图1 离散数学知识模块和各专业课程之间的关系
2 离散结构的建模是离散数学用于解决计算机学科实际问题的重要手段
模型是人们为了某种目的,运用一定的手段对某种事物或过程所作的一种既突出其特点和规律,而又比较简化的表现形式,这种描述可以是定性的,也可以是定量的。模型的建立主要是为了方便问题的解决。
如何让离散数学的理论知识应用于各专业课程实际问题的解决是体现离散数学价值所在的关键。这时对离散对象及其关系的建模就起到非常重要的作用。对于待解决的实际应用问题,可首先将涉及的离散对象以及之间的相互关系梳理清楚,然后抓住关键要素和关键关系抽象为离散数据结构及其关系的模型,再用离散数学的方法对离散模型求解。由此可见,离散结构的建模是离散数学的理论方法用于解决问题的重要手段。离散结构的模型构建过程是对客观世界事物的数学抽象,不仅是培养学生抽象思维能力的有效方法,而且对模型的求解更是对学生抽象思维与逻辑思维能力的综合训练[3]。
因此,培养学生对于离散结构模型的构建以及应用能力是离散数学的教学目标。
3 基于离散结构模型的构建与应用能力培养的教与学环节的组织
为了培养学生模型的构建能力和应用能力,笔者提出将具有实际应用背景的问题贯穿整个教学过程的探究式和问题驱动相结合的教学模式,整个教学环节按照“实际应用背景问题提出—知识点的切入—模型构建与理论验证—实验验证求解—知识点的延伸”过程来展开。
首先以一个有实际应用背景的问题作为教学的主线,在问题的讨论中切入相关知识点的概念以及性质,然后对实际问题展开分析讨论,教师发挥引导作用,在与学员的多次交流互动中,引导学生抓住问题的关键要素,完成模型的分析与构建过程,并通过实验环节完成验证求解,最后回到相关知识点概念以及性质,讨论知识点在其他方面的应用,让学生分组查阅资料分析解决。在教学组织环节中要注重如下几个方面。
3.1 注重引入问题的重要性
离散数学内容抽象,有很多定理公式,教学的重点应该在基本概念、基本理论与方法的应用上,因此,引入的问题就显得非常重要。问题一定要结合实际,关联已有的知识且有趣味性,能够吸引学生讨论,激发学生的兴趣和好奇心。在现有知识解决不了的情况下引出新知识。例如,数理逻辑中包含两部分命题演算和谓词演算,讲完命题演算要进入谓词演算的学习,两个内容之间如何过渡,如何设问引出谓词演算的知识点。教师可通过苏格拉底三段论经典逻辑推理案例引入,这个推理的正确性是人们所共知的。教师可提出能否用命题逻辑解决?针对学生在解决问题中出现的矛盾和对立观点,引导学生分析讨论发现用命题演算并不能证明其正确性,从而切入谓词的基本概念以及推理准则,即谓词演算逻辑等价式以及逻辑蕴涵式等知识点。
引入问题应该易于学生模型的构建,体现模型构建的过程。苏格拉底三段论符号化形成命题公式并不能证明其正确性,必须在有了谓词演算知识的储备下,重新进行模型的构建,即符号化为谓词公式,再利用推理准则,即离散数学的方法,去证明其正确性。整个教学以问题为驱动,以问题为主线,构建授课内容的结构框架。
3.2 教学过程中充分体现“双主”地位
教学过程的中要注重学生和教师的“双主”地位。所谓“双主”就是在发挥教师的主导性作用的同时也要发挥学生的主体性作用。教师在教学过程中应注重施教策略,优化教学过程,激发学生的求知欲,开展多种形式的互动调动学生学习的热情。教与学的互动方式包括教师与学生分析讨论、实验环节、学生与学生之间的交流等一切利于教学的互动。教师在发挥主导作用的同时需适时指导学生并给予学生必要的协作和帮助,强调学生的主体地位并不是放任学生不管,教师还需适度调控把握教学节奏,做到“收”和“放”并重。学生作为学习主体,需要积极参与教学组织过程中的多种互动,并且要投入学习热情。学生既要交流思想,也要动手实验;不仅要关心问题的答案,更要关心解决问题的过程[4]。
3.3 强调离散结构模型的构建以及应用能力的培养
离散结构模型的构建就是要将实际问题进行抽象,抓住问题的关键点以及关键要素,利用离散数学理论知识进行符号化、形式化,抽象出问题的本质,建立问题的模型,并给予求解和验证。我们以一个经典案例——中国邮政问题[1]来说明离散结构模型的构建过程。
案例:中国邮政问题。一个邮递员从邮局出发,到所管辖的街道投递邮件,最后返回邮局,若必须走遍所管辖街道中每一条街至少一次,则怎样选择投递路线可以使得所走的路程最短?
将经典案例作为整个课程的主线,给出实际街道图以及相关的数据,和学生一起分析。想要解决问题首要任务就必须进行抽象,也就是建模。建模过程按照4个步骤进行,首先,模型准备。要了解问题的实际背景,搜集必需的各种信息,尽量弄清对象的特征。邮政问题涉及的对象包括邮递员、街道、投递点、邮件。各个对象的特征,例如,街道的名字、街道的长度是街道的特征。第二步,模型假设。根据对象的特征,对问题进行必要的、合理的简化,抓住关键对象和关键特征,是建模至关重要的一步。从实际问题出发,关注的焦点应该在邮局、街道以及街道的长度。第三步,模型构成。根据各个对象之间的关系以及对象的特征规律,构造模型关系结构。根据图论前面知识的探讨,必定要将街道转为图中的边,街道与街道之间转为图中的点,形成了一个关于边的赋权图(为了说明问题方便,假设每条街道权值为1),如图2(a)所示。因此,整个邮政问题就转化为图论的问题。用图论的语言来描述:在这个边赋权图中,能否找到一条闭的拟路径C,使C包含图中的每条边最少一次且C的权值最小?
离散结构的模型构建好以后,最后一步,利用离散数学方法模型求解。根据用图论的语言描述邮政问题,联想到应该用欧拉图知识来解决。如果图中一条经过所有顶点、所有边的闭路径即为欧拉图。判断欧拉图的充分必要条件所有顶点的度均为偶数。如果街道赋权图是欧拉图那么问题迎刃而解。如果图2(a)不是欧拉图,则必然有些街道要被重复走过才能回到原点。解决问题的思路并不复杂:在奇数度的顶点间加边或者路径(表示重复走原图上的边或者路径),使其成为欧拉图。为达到使C权值最小的目的,应当选择权值尽可能小的添加边或路径,如图2(b)所示。如何使得所加边的长度最小,归结为求奇数度之间的最小匹配。
基于上述的分析,解决邮政问题的基本步骤是:
(1)判断街区是否为欧拉图,若是,则问题迎刃而解;
(2)若不是欧拉图,则找出所有奇数度的顶点(由握手定理知奇数度的顶点必为偶数个),令其集合为X;
(3)对X中的顶点两两作检查,计算两顶点之间最短路径的权值,并以小于或者等于关系排序;
(4)在具有最小权值的一对顶点(例如{x,y})间加边,取该权值为新添加的边的权值。在权值序列中删除所有与顶点x、y相关的权值;
(5)回到步骤4,直到权值序列为空。
(6)通过Fleury(佛罗莱)算法来求解最短闭的拟路径。
完成第(5)步,便得到一个所有顶点度数均为偶数的连通图,即欧拉图,且添加的边的权值和是最小的。邮递员从邮局出发,走遍整个欧拉图,便走遍所管辖街道中每一条街至少一次。到这里只是解决了街道至少走一次,要保证走的路最短还未解决,因此还需完成第(6)步。
从上述的例子不难看出模型构建的方法,首先摸清待解决问题的背景,分析涉及的各类对象以及它们之间的关系;其次,抓住主要对象以及关键点和关键要素进行数学抽象,构建关系模型;最后利用离散数学中欧拉图的知识点去解决构建的模型。整个过程锻炼了学生的抽象思维能力、逻辑思维能力,抽象出的模型又能方便地解决问题。
3.4 通过实验环节解决问题提高应用能力
通过模型构建,学生将概念、定理和性质变成用于解决问题的重要方法。解决邮政问题的思路以及方法很明确了,最后还需要通过实验环节计算出最终的方案,即需要通过计算机编程体现解决问题的思路。实验环节和模型构建过程同等重要,都考验学生计算机动手能力。实验环节可以加深对抽象概念和知识的理解,让学生进一步理解离散数学在解决计算问题中的作用,并提高其利用计算机解决问题的能力,同时,通过解决问题的成就感对提高学习兴趣也有很大的帮助,这是一个相辅相成,循环促进的关系。
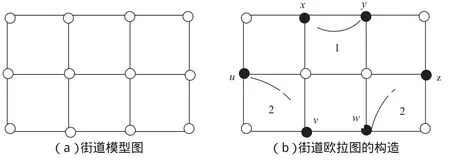
图2 赋权图街道
4 总结
离散数学的教学目标是培养学生离散结构模型的构建与应用能力,使学生深入理解并学会使用这些模型解决实际问题。将离散结构模型的构建过程融入到教学过程,使学生感受到理论知识可以用于解决实际问题,提高学习该课程的兴趣以及主观能动性,培养了学生抽象思维能力、逻辑思维能力以及解决问题能,为后面的专业课夯实了基础知识的储备。
[1]王元元.离散数学教程[M].北京:高等教育出版社,2010.
[2]王彩玲.问题驱动模式下离散数学小班化教学方法探讨[J].计算机教育,2012(15):19.
[3]徐洁磐.应用型计算机本科中离散数学课程目标定位与课程改革的探讨[J].计算机教育,2010(5):6-9.
[4]薛占熬.论“双主”在离散数学教学过程中的作用[J].计算机教育,2011(18):37-40.
