突显能力培养的离散数学逆向案例教学改革探索
2018-01-27徐周波古天龙
徐周波,古天龙,常 亮
(桂林电子科技大学计算机与信息安全学院,广西桂林541004)
2015年我国成为《华盛顿协议》正式会员,工程教育认证为广大工科院校开展工程应用型人才培养给予了方向性指导,强调工程应用型人才必须具备对复杂工程问题的建模、设计、分析和求解的能力。随着经济发展方式的转变、产业结构的转型以及加快推进创新型国家的建设,2017年教育部启动了“新工科”发展研究工作,提出着眼于未来新技术与新产业的人才需求,培养具有可持续竞争力的创新人才。课程是高校实施教育的核心,课程教学效果的好坏直接影响着人才培养的质量。近年来,我国一直以课程改革的方式来提高整体教育质量。2013年在深圳会议发表的“计算思维教学改革宣言”意味着新一轮大学计算机课程改革的核心导向为计算思维能力的培养[1]。计算思维是指运用计算机科学的基本概念来求解问题、设计系统和理解人类行为,包括一系列广泛的计算机科学的思维方法[2]。在课程教学实施中培养学生计算思维能力、创新能力以及快速学习新事物能力是促进学生能力提升的有效途径,也是近年来课程改革关注的焦点[3-4]。
作为计算机类专业核心基础课程的离散数学不仅是计算机后续专业课程(如数据结构、操作系统、数据库系统原理、人工智能、数字逻辑等)的重要基础,也是培养学生计算思维能力的重要基础课程。但在实际教学中,任课教师更多地关注学科知识的传授,缺乏从专业课程体系角度和计算思维能力培养的角度来讲授课程,致使学生错误地认为离散数学课程是一门纯粹的数学课程,枯燥抽象,难以引起学习兴趣;此外,学生即使掌握了基本概念和定理,但仍缺乏知识迁移能力,难以运用知识解决问题。
1 基于课程定位,强调离散数学在专业课程中的应用
离散数学是研究计算机科学的数学理论基础,是研究离散量及其相互关系的一门学科,包括集合论、数理逻辑、抽象代数和图论四部分教学内容。离散数学课程在ACM和IEEE-CS制定的计算机科学教程以及我国高等学校计算机科学与技术教学指导委员会的计算机专业规范中均处于核心地位。
在课堂教学中需要使学生理解离散数学课程的重要地位,在引入离散数学教学内容之前,首先要让学生明确学习离散数学课程的目的,即培养运用离散数学中的基本概念、思想和方法去构建问题的抽象模型并在此基础上培养设计、分析和解决问题的能力,以及创新能力和快速学习新事物的能力。数字电子计算机本身是一个离散结构,只能处理离散的或离散化了的数量关系。因此,无论是计算机科学本身,还是与计算机密切相关的现代科学研究领域,都面临着如何对离散结构建立模型或者将已用连续数量关系建立起来的模型离散化,再由计算机加以处理和实现的问题。而离散数学正是其不可缺少的理论工具,需要在课程教学过程中引入案例让学生逐步体验领会并学会应用。
其次要让学生明确离散数学与专业课程体系中其他课程之间的关系,如图1所示。如命题公式可与数据结构中的二叉树相联系;关系可与数据库系统原理课程中的元组、表、关系代数运算等联系在一起;抽象代数可与幺元和程序设计中赋予变量的缺省值联系在一起;有向图的连通性可与操作系统中的进程死锁联系在一起。使学生在学习学科知识的同时领会其在其他专业课程中的应用,激发学生对知识迁移的感性认知,促进学生计算思维能力的培养,进而提升学生对离散数学课程的重视度和学习兴趣。
2 围绕课程教学目标,实施逆向案例教学,落实学生的计算思维能力培养
作为计算机类专业核心基础课程的离散数学,其课程教学不只是简单地传授给学生学科知识,更重要的是培养学生运用所学理论去构建问题的抽象模型并在此基础上设计、分析和解决问题以及快速学习新事物的能力。然而,目前国内各高校普遍存在压缩课时的现象,教学内容和教学学时的矛盾致使教师普遍在课堂教学中进行“满堂灌”,而无暇顾及课程目标中的能力培养,课程目标成为抽象的口号,学生学习课程之后也难以将离散数学的知识迁移到具体应用中。案例教学是一种传统教学模式,通过合理有效的案例能有效减轻学生对抽象内容的认知负荷,但因其渐进式的案例分析,提高学生解决新问题的能力及知识迁移能力的效果较差。逆向教学则将学生从单纯的知识接收者转变为探究者,让学生在探究的过程中学会独立思考[5]。因此,将案例教学法与逆向教学法相结合,有利于培养学生的问题求解能力和知识迁移能力。
2.1 逆向案例教学设计
在离散数学课程教学过程中引入逆向案例教学法,基于“提出问题—分析问题—引入概念—抽象建模—设计分析—程序设计”的教学设计思路,设计合理的涵盖课程教学内容的教学案例。在学生分析思考如何求解问题的同时,引入所需知识点;在解决问题的过程中领会相应知识点在实际应用和后续课程中的作用,从而提升学生运用理论知识对问题进行抽象建模、设计、分析和求解的能力,通过算法设计分析,进一步提出解决方案的改进,提升学生的动手能力和知识迁移能力。
由于离散数学课程一般开设在大学第二和第三学期,为此在教学案例设计时需考虑学生已有的知识体系和接受能力,保留一定的拓展空间,使其适应于不同水平的学生。以图论部分为例,在表1中,我们以“能力培养”为出发点,通过提出问题、分析问题、问题抽象建模、问题的算法设计与分析等逐步引入教学大纲中的知识点,并按逆向案例教学法从简单到复杂设计每一个案例。培养一名计算机专业学生,除了培养其强大的“内功”之外,还必须培养能发挥其内功的“外功”,即既需培养学生具备扎实的学科基础理论知识,又需培养学生具有使用现代工具解决问题的能力。因此,在每一个案例的建模求解之后,安排学生在课后去编程实现,这不仅提高了学生的计算思维能力和程序设计能力,而且也加深了学生对知识的理解,有利于提高学生的自学能力。但在离散数学课程中使用一种特定的编程语言容易干扰并分散学生对于算法问题求解核心部分的注意力。为此,选择已被广泛普及应用于计算机教学的Raptor(therapid algorithmicprototypingtoolfororderedreasoning,用于有序推理的快速算法原型工具)来编程实现每一个案例的算法。Raptor是一种基于流程图的程序开发环境,通过绘制算法流程图而不是某一具体的计算机语言来实现算法,此工具还可以将绘制的流程图直接翻译成具体的一种计算机语言,如C++语言、C#和Ada,便于学生对具体计算机语言的后续学习。通过此部分的实践,不仅可以让学生体会到算法设计对问题求解有效性的评估,而且引导学生完成了“分析问题—抽象建模—算法设计、分析—程序设计”的完整流程,培养了学生的计算思维能力和学习新事物的能力。
2.2 逆向案例教学实施过程
基于逆向案例教学设计思路,在课堂教学过程中按简单到复杂将各个案例逐个引入,通过提出问题、分析问题、问题抽象建模、问题的算法设计与分析等方式逐步引入教学大纲中的知识点。例如,为引入图论的基本概念和基本定理,从哥尼斯堡七桥问题着手提出问题,并让学生试着解决问题。只在地图上寻找答案可能会遗漏某些可行的方案,以此为开端,引入图论的方法来求解该问题。首先对问题进行分析,将陆地和岛屿看成图中的顶点,将桥看成连接图中顶点的边,以此引入图论中的一些基本概念和方法。然后建立原问题的抽象模型——欧拉图的判定,即将哥尼斯堡七桥问题转化为在图中寻找一条欧拉回路的问题。通过引入欧拉图的判定定理,学生很快就能给出哥尼斯堡七桥问题无解的结论。通过对原问题的抽象表示并应用图论中的理论进行设计、分析,让学生切实领会理论的指导意义。通过对欧拉图的学习,学生可以在课外完成“街道清扫”“巡逻维护”等路线设计问题,举一反三,巩固知识,进一步提高知识迁移能力。
3 科研反哺教学,培养学生的科学素质和创新能力
大学本科阶段越来越注重素质教育及创新能力的培养,离散数学在培养学生的创新能力和提高学生的科研素质方面都有着重要作用。教师在传授课本知识的同时,引入科研成果,拓宽教材中的知识点的应用延伸,可以进一步培养学生的探究学习能力,培养学生基本科研兴趣和创新能力。
例如,在命题逻辑中,命题公式类型的讲解一方面可以引入人工智能中历史悠久的可满足性问题(SAT)和约束可满足问题(constraint satisfyproblem,CSP),列举典型的SAT和CSP案例,如地图着色问题、机器人穿衣问题、无线电链路频率分配问题等,给出SAT和CSP的算法框架,并提供一些参考文献供学生课后学习,拓宽学生视野。另一方面可以从算法自动执行的角度来分析命题公式类型的判定算法,算法的好坏通常由时间和空间复杂度来衡量。从存储空间角度来看,若用完全二叉树或二维数组来存储命题公式A=x1·x2,则存在大量重复的0和1,如图2(a)、3(b)所示。利用图的同构性,将完全二叉树中所有同构的图(子图)合并,并利用命题公式基本定律,去掉无关命题变元,得到新的结构,称之为二叉决策图(binarydecision diagram,BDD)[6],如图2(c)所示。可见,利用离散数学中的理论知识得出的BDD结构具有更好的存储效率。后续结合电路设计实际案例来详述BDD在简化和验证电路设计中的优越性以及在介绍经典的最短路径算法Dijkstra后,引领学生思考可否“并行”求解多条最短路径问题,并给出基于BDD的“并行”求解多条最短路径算法。通过将科研反哺于教学,不仅能够培养学生的逻辑思维能力、分析能力和创新能力,而且还易于让学生意识并体会到知识的巩固、提升在科研领域和生活实际中产生的重大影响。
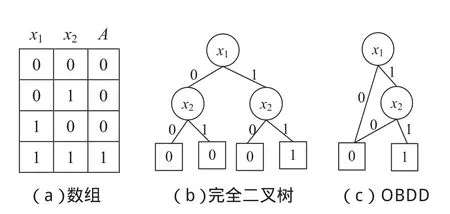
图2 对于命题公式A=x1·x2的存储表示
4 结语
面对当前和未来战略新兴产业的人才需求,离散数学作为计算机专业的核心基础课程,在课程教学上更应侧重学生的计算思维能力培养和可持续发展学习能力的培养。通过逆向案例教学法,从专业课程体系的角度和计算思维能力培养角度设计教学案例,在传承课本知识的同时,注重科研反哺教学,这不仅有利于学生感性认知离散数学课程的核心地位,提升学生的学习兴趣,为学生继续后续课程学习以及从事科学研究和进行工程应用开发奠定坚实的理论基础,也有利于培养学生知识迁移能力、创新能力和解决实际问题的能力。
