解析大衍筮法及易卦的蓍占概率

孙 涤

一、邵康节的“加一倍法”

北宋的易学大家邵雍在易卦整体结构的探究上达到了超越前贤的高度，他制定的“伏羲六十四卦圆方图”是一座巅峰。其为易卦排序所遵循的方法，历来人称“加一倍法”，然而对内中的机理和逻辑，尚无一致和妥帖的解说。比邵雍略晚的大儒程颢算是慧眼独具，曾评述道：“尧夫之数，只是加一倍法。以此知《太玄》都不济事。”他认为“加一倍法”要比扬雄的太玄数更高卓。邵雍听了程颢这番“识货”的话，惊而抚其背曰：“大哥，你恁聪明！”*蔡元定亦云：“康节之学，虽作用不同，而其实则伏羲所画之卦也，明道所谓加一倍法也。”

可是“加一倍法”更深层次的奥义，前代几乎无人述及的，是邵雍把六十四个易卦“加了一倍”，拓展成(26)2=(64)2，计有4096种变化。因为无论阴爻还是阳爻，又有可变与不可变之分。在此有必要先弄清楚，邵雍之“加一倍法”的真实含义不是简单地乘二加倍，而是二乘方。

欲准确把握“加一倍法”的真意，尤其要在应用上避免偏误，还得从解读“大衍筮法”入手。由大衍筮法筮得的是四个随机数：6、8、7、9，其中6和8代表阴爻(6为可变之阴爻，8为不可变阴爻)，9和7代表阳爻(9为可变之阳爻，7为不可变阳爻)。这就是说，同为阴爻，有6和8两种可能，同为阳爻也有9和7两种可能。如此，每一个卦的六条爻，又包含着26=64种变化。六十四个易卦总共有4096种变化。以三爻的坤卦为例，可以是666(全是可变阴爻)，也可以是888(全为不可变阴爻)，也可以是668、686、866、688、868、886，一共有23=8种变化。坤上坤下的六爻坤卦是两个地卦的叠加，故有8×8=(23)2=64种变化。

在此之前，先来回顾一下人类思想史上的一个著名片段，为其佐证。引进新的解析工具和更新认知的观念方法，对于易学的现代探索，有着非同寻常的意义。

二、“加一倍法”与二进制算法

莱布尼茨在1703年4月1日读到了在中国传教的耶稣会士、法国人白晋*白晋(Joachim Bouvet)，1656年生于法国勒芒市，1686年被法皇路易十四选派为首批六名来华耶稣会士之一，于1688年抵达北京。作为亲善大使，白晋直接沟通路易十四和康熙两位君主，并深受器重，在《易经》探究上同康熙的切磋尤其频繁。他通过与莱布尼茨的通信往返切磋，对二进制的开创有着(间接的)历史性贡献。雍正八年(1730)卒于北京。从北京寄给他的邵雍所制“伏羲六十四卦圆方图”，顿时明白，“加一倍法”与他专研的二进制算法是高度契合的。白晋是当时屈指可数的汉学大师，他向莱布尼茨介绍了《周易》和八卦的系统。莱布尼茨认为阴、阳基本上就是他终身在探究的二进制的汉文明版本，并尝试用二进制算法替八卦(三爻)和六十四个易卦作数字“身份认定”，从而排出了卦序的编号。

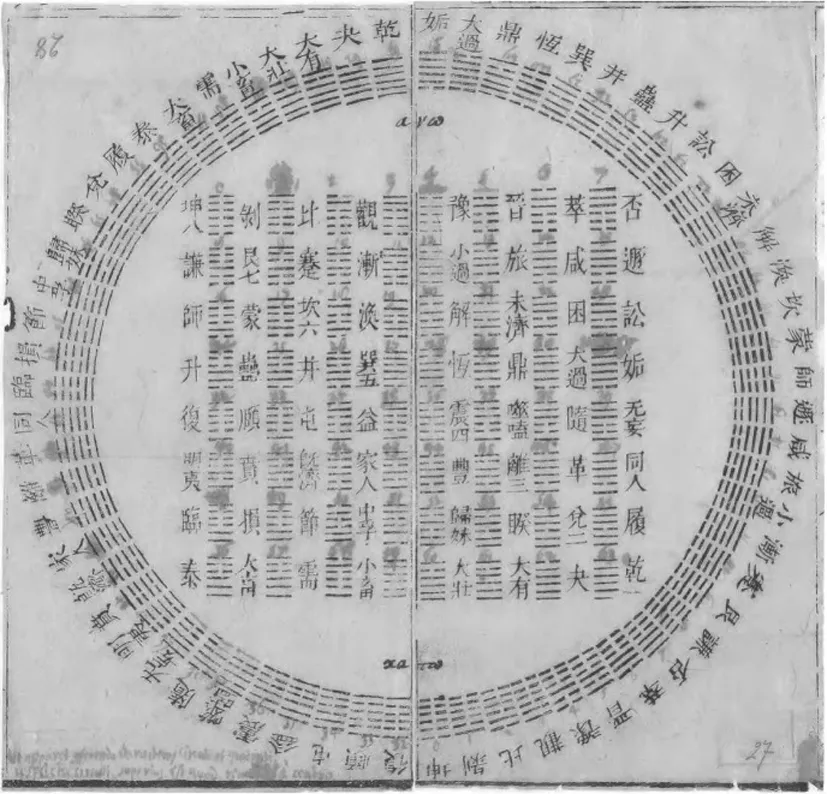
图1

莱布尼茨专研和制定二进制算术的努力始于1670年代，他的相关论文则正式发表于1703年，而且终其一生都在不断推进和改善。1697至1707年间，莱布尼茨和白晋通过书信往返，在《易经》探索上有长期的交流，其中至少有十五封书信现保存在德国图林根的图书馆和汉诺威的莱氏文献馆。莱布尼茨怀着高度兴趣研读了白晋邮寄给他的易经《先天图》(即由邵雍率先披露、托名伏羲的《伏羲六十四卦次序图》和《伏羲六十四卦方位图》)，并迅即给出了八个三爻卦和所有六十四个易卦的二进制编号(见图1)*图1为莱布尼兹所见到的邵雍“伏羲先天圆图”和“伏羲先天方图”，系由耶稣会士白晋随信寄给他的原图。该信1701年11月4日写于北京，估计在1702年秋间送达德国汉诺威，但直到1703年4月1日方才为莱布尼茨读到。莱氏阅后大喜过望，因为易卦结构明显展现出其蕴涵的数理与自己专研了二十余年的二进制算法如出一辙。莱布尼茨于次日立即回复，详细记录了白晋有关这两个系统具有同一性的发见以及自己的一些思考。随后，莱氏于5月5日寄出他受到此图启发后修改完成的里程碑意义的论文，同年发表于法兰西皇家学院学刊。该论文的初稿曾于两年前投稿法兰西皇家学院，由于缺乏应用实例和历史依据，被质疑其可用性而遭到搁置。白晋提供的易经图及应用佐证，帮助莱氏完成并成功发表了论文。。

在白晋提供的邵雍伏羲先天图的启发下，莱布尼兹从易卦的卦象得出了二进制编号，不禁为之惊喜。他在给白晋的回信中写道：“我发现二进制数是二十年前。到今天我才发现……中国人在四千年前，已经了解到0与1的二元数学了。”而他发表于1703年的那篇划时代论文的完整题目为《二进制算术的解释——只用0和1符号，兼及它的一些应用，以及对中国古代伏羲图像的破解》。足见莱布尼茨关于二进制的思考，与邵雍的象数和图的确是息息相通的。

那么，莱布尼兹是怎样用他首创的二进制算法来得到易卦的排序的？同“加一倍法”一般无二，莱氏以阳爻为1，阴爻为0，自上而下逐爻加倍来算出的。最简单的,如坤卦的000000，排序为0(0×20+0×21+0×22+0×23+0×24+0×25=0)；乾卦111111的排序则是63(1×20+1×21+1×22+1×23+1×24+1×25=63)。 然而，既济的010101，六条爻自上而下为0、1、0、1、0、1，排序又是多少呢？是0×20+1×21+0×22+1×23+0×24+1×25=42。如此可以很容易验证，图1里莱布尼茨给出的屯卦的010001和蒙卦的100010的排序分别是34和17，而否卦的111000和泰卦的000111排序则分别为7和56(结果见图2)。

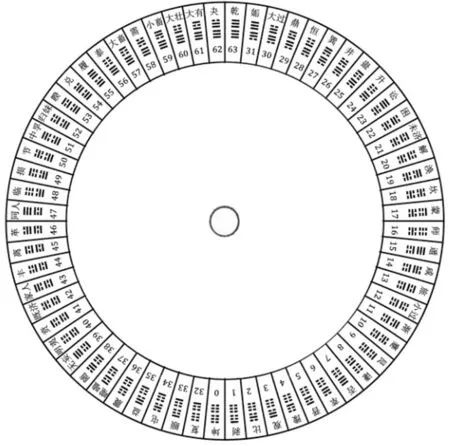
图2

从坤卦0、剥卦1直到姤卦31逆时针排成圆图的右半圈，然后从复卦32、颐卦33直至乾卦63，顺时针排成圆形的左半圈。邵雍的伏羲先天圆图实为“两仪相逆”排列的结果*见图1中莱布尼茨手写的页码。27、28是倒着写的，表明莱氏已深谙“两仪相逆”之理。。非常有意思的是，经过圆心的连线联接的两卦成为一对，其排序之和必为63。这样构成的32对卦里，只有8对(坤乾、小过中孚、坎离、大过颐，以及否泰、渐归妹、未济既济、蛊随)，在《周易》里原来就构成对卦，其余的24对都不是。这又是为什么呢？

再来看莱布尼茨对八个纯卦(三爻)的排序：地0—山1—水2—风3—雷4—火5—泽6—天7，与邵雍在伏羲先天方图里的排序(汉文数目字)正相逆。但是，两种排序的相对位置则是相同的。若莱氏以阴爻为1、阳爻为0的话，排出的八卦序就几乎跟邵雍完全一样，将是地7—山6—水5—风4—雷3—火2—泽1—天0。生活在欧陆文明的人，单一起源的宇宙观，犹太基督教的单一神主宰的范式是非常强有力的。莱布尼茨因而只能作另一选择，即以阳爻为1，为至上的单一神所代表的宇宙最高的秩序和善；而以阴爻为0，表示混乱、涣散、虚无、不完善、甚至邪恶，总之，没有结构可言。况且，天排在7，与西方固有的价值信仰并无出入，7在他们是个“圣数”，上帝造了六天的世界之后，第七天(星期天)是个休息日。

在莱氏排序里，山卦的排序为1。那么山1又是如何计算出来的呢？山卦的二进制代码是100，按规范的二进制算法，其排序应当是0×20+0×21+1×22=4。莱布尼茨作出的“妥协”，是倒过来计算的，即自上而下逆向地“加一倍法”。也就是，以上爻位为初位，乘数为20=1，而以初爻位为最高的第三位，乘数为22=4计算出来的，结果序号才可能是1×20+0×21+0×22=1。问题是，倒过来看还是山卦吗？它不就成了序号为1的雷卦001？同理，邵雍与莱氏排序中的雷4，按照规范的二进制算法，排序理当为雷1；而风3和泽6则分别应当是风6和泽3。换言之，八卦里面倒有一半排序发生了问题(见图3)*该图摘引自莱布尼茨于1703年发表于法国皇家学会学刊的二进制算法的论文，该论文在科学史上具有里程碑的意义。其中莱氏替被他称作二进制算法源头的中国远古圣贤伏羲氏智慧的八卦，排了卦序。可以看到，莱氏所作的“妥协”，是他把卦象竖了起来，这在伏羲先天图里是未曾有过的。结果，排为1的卦象究竟是山卦还是雷卦，于是含混起来(排序为3、4、6的卦象也是如此)。这个妥协带来的含混产生了一系列后果，引致各种误导。譬如，对太极图里八卦的方位解读问题。这里讨论的自下而上与自上而下的差别，在八卦方位的环图中，则是卦象究竟应该从外向环心看，还是从里朝环周看？对于莱氏竖着的卦象，问题却变为卦象应该是从右到左，还是从左到右来看？。

图3

这个问题蔓延到全部的六十四个易卦。譬如，否卦111000的排序应当是7(莱布尼茨的)，还是56(二进制数值法的)？与否卦成对的泰卦，排序究竟是7还是56？再以《周易》里的屯卦3—蒙卦4为例分析，莱氏及邵雍的排序，是屯卦34—蒙卦17，而在正规的二进制数值排序里，理应为屯卦17—蒙卦34！

这个困扰的肇因，绝不仅仅是简单的算法技术问题，而是思考观察的分析框架所致，背后有着文化和观念的深厚积淀。莱布尼茨受此困扰，放弃了继续深入挖掘。但是谁又想得到，这个问题竟得拖延三百余年，到今天才来解答呢？笔者将在另处，以“易学的现代诠释”、“易卦结构与二进制的关系”等为题，展开深入辨析。

三、大衍筮法辨析

大衍筮法又称揲蓍法、蓍占，或直接称作周易占法，是载入《周易》原文的唯一筮法。历朝历代的易学家们口授心传的依据，是《易传·系辞》里的一段原文(《大衍之数五十》章及原注)*《易传·系辞上》“大衍之数五十”章：“大衍之数五十，其用四十有九。分而为二以象两，挂一以象三，揲之以四以象四时，归奇于扐以象闰，五岁再闰故再扐而后挂。天数五，地数五，五位相得而各有合。天数二十有五，地数三十。凡天地之数五十有五，此所以成变化而行鬼神也。乾之策二百一十有六，坤之策百四十有四，凡三百有六十，当期之日。二篇之策万有一千五百二十，当万物之数也。是故四营而成易，十有八变而成卦，八卦而小成，引而伸之，触类而长之，天下之能事毕矣。”。

筮占之“筮”，从竹从巫，“竹”代表草木，“巫”代表占卜。筮是用植物进行的预测，卜则是用动物做的预测。蓍占以蓍草为工具来指导“风险决策”，而卜则以龟甲、兽骨作为工具。《说文》有曰“筮，易卦用蓍也”，反映了西周时代就很流行的蓍筮文化。蓍占在早期是与龟卜并重的。《周易》大衍筮法得到重视，得以广泛流传和使用，与孔子及其门人作《易传》并推崇蓍占有很大的关系，龟卜的方法渐渐失传了。

图4

筮占所用的道具是蓍草，一种长于西伯利亚和中国北方的多年生直立篙类植物。河南淮阳的伏羲太昊陵有蓍草园，但蓍草只生于那个园地的说法，并不确实。筮占是用50茎经过香薰的、长约尺许的干蓍草来进行的占卜，因其方法基于“大衍之数”，又被称为“大衍筮法”。本质上，筮占是借“植物灵性”来“沟通天意”的(图4)。

大衍筮法是八卦系统的四象筮法，得到的6、7、8、9四个数，6为可变之阴爻，9为可变之阳爻；7为不可变之阳爻，8为不可变之阴爻。这里的“可变”有待变之意，阴阳转换——6待变为7，9待变为8。

就其实质而言，大衍筮法的过程是一个“随机发生器”。问题在于，得到6、7、8、9这四个随机数的概率分别是多少呢？下文的分析推导得出结论：同为阴爻，得到可变阴爻6的概率是1/16，得到不可变阴爻8的概率则为7/16；同为阳爻，得到可变阳爻9和不可变阳爻7的概率，分别是3/16和5/16*邵雍曰：“大衍之数，其算法之原乎？是以算数之起，不过乎方圆曲直也。乘数，生数也。除数，消数也。算法虽多，不出乎此矣。”(邵雍著，黄畿注，卫绍生校理：《皇极经世书》卷七上《观物外篇上·河图天地全数第一》，郑州：中州古籍出版社，1993年，第311页)沈括《梦溪笔谈》卷七《象数一》：“《洪范》‘五行’数，自一至五。先儒谓之此‘五行生数’，各益以土数，以为‘成数’。以谓五行非土不成，故水生一而成六，火生二而成七，木生三而成八，金生四而成九，土生五而成十，合之为五十有五。唯《黄帝素问》：‘土生数五，成数亦五。’盖水、火、木、金皆待土而成，土更无所待，故止一五而已。画而为图，其理可见。为之图者，设木于东，设金于西，火居南，水居北，土居中央。四方自为生数，各并中央之土，以为成数。土自居其位，更无所并，自然止有五数，盖土不须更待土而成也。合五行之数为五十，则大衍之数也。此亦有理。揲蓍之法：四十九蓍，聚之则一，而四十九隐于一中；散之则四十九，而一隐于四十九中。一者，道也。谓之无，则一在；谓之有，则不可取。四十九者，用也。静则归于一，动则惟睹其用，一在其间而不可取。此所谓‘大衍之数五十，其用四十有九’。”(沈括撰，胡道静校注：《新校正梦溪笔谈》，北京：中华书局，1957年，第78页)。

大衍筮法产生的随机结果，不加细辨的话，很容易误以为得到这四个数的几率是相等的，均为1/4。或者注意到了大衍筮法生成一爻需经过“三变”，三个阶段的组合之后，得到6、7、8、9四个数的概率分别为1/8、3/8、3/8、1/8。虽说这几种替代大衍筮法的简化办法，得到阴爻和阳爻(可变+不可变的)的概率，都还是各半(1/2)，然而其间微妙的变化，可以导致非常悬殊的结果。

厘清大衍筮法获得6、7、8、9四个数的(随机)准确概率，非常之有必要。毕竟，在《易传》里得到奠基的卦辞、象辞、爻辞，以及各家的诠释，所依据的都是大衍筮法的蓍占结果*诸多占卦预测的方法里，大衍筮法始终占据着主导地位。《左传》、《国语》中记载的二十多则先秦筮案均为大衍筮案。后世以预测精确著称的管辂、郭璞等高人所用的无不是大衍筮法，北宋的陈抟和邵雍用的也都是大衍筮法。近代如易学大家尚秉和先生的《筮案辑存》，数十则案例无一不是大衍筮案。。不严格按照大衍筮法生成爻和卦的概率，会对易卦的诠释造成很大的偏误。其他的概率，包括变通简化方法得到的，如果不作相应的调整，很可能导致谬以千里的解卦结论和估测判断。

历来对大衍筮法产生的随机结果有种种偏误的理解，并不奇怪。大衍筮法的过程庄严繁琐，不只令现代人感到茫然，古人也一定觉得很挠头。朱熹不愧为不世出的大学者，他经过执著精细的研析，暗示出了6、7、8、9四个数，即可变之阴爻、不可变之阳爻、不可变之阴爻、可变之阳爻的得到概率是不平衡的，即所谓“可变之爻常少而不可变之爻常多”的道理*朱熹曰：“六爻皆不变，占本卦彖辞。”(朱熹撰，苏勇校注：《周易本义》附录二《易学启蒙·考变占》，北京：北京大学出版社，1992年，第234页)他又认为，“有天地自然之易，有伏羲之易，有文王周公之易，有孔子之易。自伏羲以上，皆无文字，只有图画，最宜深玩，可见作《易》本原精微之意。文王以下，方有文字，即今之《周易》。然读者亦宜各就本文消息，不可便以孔子之说为文王之说也”(朱熹撰，苏勇校注：《周易本义》附录一《周易本义附图·卦变图》，第204页)。而弄明白“伏羲卦象”要比读懂《周易》通行文本更为重要。他说：“必欲知圣人作《易》之本，则当考伏羲之画；若只欲知今《易》书文义，则但求之文王之经、孔子之传足矣。两者初不相妨，而亦不可以相杂。”。

在其名著《周易本义》卷首《筮仪》篇中，朱熹对大衍筮法的过程有相当详尽的描述和注解。他说，四个数的概率之所以不平衡，是因为大衍筮法过程的端始，“取其一策，反于柜中”——“但用四十九蓍耳”，即大衍之数50，用的是49根蓍草的缘故*大衍筮法用49根蓍草，因此变化非常丰富奇谲。设若“取其二策，反于柜中”，即用的是48根蓍草的话，变化就要简单得多，在那种情况下得到6、7、8、9四个随机数的概率才是1∶3∶3∶1。。

第一变，“挂一”之后，随机分成两刻的蓍草剩下48茎。从每一群蓍草里分别取走4茎的整倍数后，再剔除其余数——或1或2或3或4茎，剩下了44茎或40茎。在第二变“挂一”之后，分别成了43茎或39茎。“归奇”即剔除余数(3或7)后，从43茎剩下的是40茎或36茎，概率各半；从39茎则剩下36茎或32茎，概率也是相等的。然后是第三变，“挂一”之后则成了39茎、35茎或31茎。“归奇”即剔除余数(3或7)后，从39茎剩下36茎或32茎，从35茎剩下32茎或28茎，从31茎则剩下28茎或24茎，概率也是各占其半。以朱熹的话来讲，是“奇耦各得四之二焉”(3=1+2或2+1；7=3+4或4+3，各在四种可能性里占了两种)。

然而其中的奥妙，是第一变所得到的“奇耦”，是否也“各得四之二焉”呢？非也。其关键就在于“但用四十九蓍耳”。

三变之后所剩下的24茎、28茎、32茎、36茎蓍草的4的整倍数，就是6、7、8、9(扐数)。得到6、7、8、9的概率，结果分别为1/16、5/16、7/16、3/16，其中得到7的概率是5/16=1/16+1/16+3/16；得到8的概率是7/16=1/16+3/16+3/16。

第一变在概率上的变化，导致了6、7、8、9随机结果的比例是1∶5∶7∶3，而非4∶4∶4∶4。同样的，2∶6∶6∶2也不准确*设若“存体”的蓍草茎数不是1，而是2的话，那么产生6、7、8、9这四个随机数的概率分布将为八分之1∶3∶3∶1。这个概率分布是自唐代以来民间所习用的“摇钱筮法”等简化方法产生的结果。作者把各个可能的“存体”数为初始值的大衍筮法的结果列表如下。假设：1.“存二”(50策蓍草里先取出2策不用)，得到四种爻的概率是多少？2.“存0”，即从50策蓍草先取出0策不用的话，又是怎样的结果？3.“存三”，即从50策蓍草先取出3策不用的话，又是如何的呢？结果如下表所列：。这个道理，用概率分析的工具“决策树”(三个阶段)来描述，应当能一目了然(见附录二)。

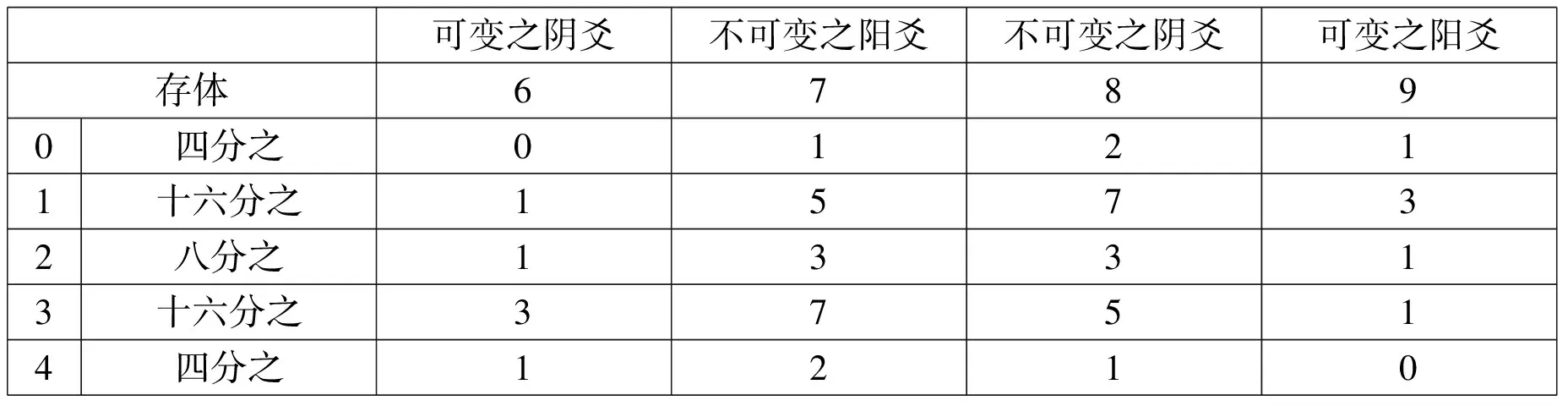
可变之阴爻不可变之阳爻不可变之阴爻可变之阳爻存体67890四分之01211十六分之15732八分之13313十六分之37514四分之1210

不过要做出一个简单的随机发生器来精确模拟“大衍筮法”的概率，却有点复杂。由于世界上不存在正十六面体，无从设计出一个简单的“骰子”，来随机地获得概率为1/16、3/16、5/16和7/16的四个随机结果。作为替代，笔者建议的办法，是用两枚钱币(fair coin)进行两次抛掷，从而得到一条爻。其随机概率可以列表如图6。重复六遍，结果得到六条爻，便构成一个六爻易卦(图5)。

第一次抛掷第二次抛掷揲数涵义概率头、头头、头6可变阴爻1/16头、尾7不可变阳爻1/16尾、头7不可变阳爻1/16尾、尾8不可变阴爻1/16

其余，即头、尾头、头7不可变阳爻3/16头、尾8不可变阴爻3/16尾、头尾、头8不可变阴爻3/16尾、尾尾、尾9可变阳爻3/16

图5

由此得到的易卦，不但知道其为何卦，而且能很清晰地明白每一条爻是可变的还是不可变的。联系《易经》、《易传》对易卦的诠释，对所得之卦的解释才有可能做到精准。

四、由大衍筮法得到的易卦概率

那么，大衍筮法得到每个易卦的概率又是如何来计算的呢？以最简单的纯阴坤卦和纯阳乾卦为例来说明。坤卦的六条阴爻，每条爻可以是可变的6或不可变的8，所以共有64种(2的六次方)变化来构成坤卦。六条爻皆为不可变(888888，数字从右至左代表初爻到上爻)的坤卦概率(7/16的六次方)，是六爻皆为可变(666666)的坤卦概率(1/16的六次方)的117649倍(7的六次方)。同理，同为六阳的乾卦，仅一条可变阳爻的乾卦977777(5/16的五次方×3/16)的概率是有四条可变阳爻的乾卦799997(5/16的二次方×3/16的四次方)的12.1倍。

大衍筮法生成每条爻是独立生成的，三变成一爻、重复六遍成一卦，因此，每爻生成的概率相互独立，与所在的爻位无关。例如，不可变阴爻8无论是在二爻位、五爻位，或任何爻位，概率都是7/16；可变阳爻9无论在哪个爻位，概率也都等于3/16。所以成卦的概率只决定于阴爻条数和阳爻条数(加起来为6)，及其可变性或不可变性。简单地说，取决于n个6或8，与(6-n)个9或7的组合。因而计算卦的概率用的也是组合，而非排列方法。

以坤卦来说，它的64种变化只有7种独立的概率，分别是n条(n=0、1、2、3、4、5、或6)可变阴爻的概率(1/16)乘以(6-n)条不可变阴爻的概率(7/16)，加权后成卦的概率为0.015625。以乾卦而言，也只有7种独立的概率，分别是m条(m=0、1、2、3、4、5、或6)可变阳爻的概率(3/16)乘以(6-m)6条不可变阳爻的概率(5/16)，加权后成卦的概率也是0.015625(见图6)。

1.5625%即1/64，说明在邵雍的“加一倍法”，得到所有的64个易卦的概率依然相等，即等概的。而每卦的构成尽管有64种变化，总共642=4096种变化，不过独立概率的数目却少得多。计算的结果表明，独立概率总共才84个(详见附录二，完整的易卦概率表)。

“附录二”的易卦概率表，是从阳爻的角度来对易卦分类，从而计算出各类卦的概率表。所有的64个卦，概率都是1/64，即1.56%。但是，1.56%的概率是如何分布为可变或不可变阳爻，可变或不可变阴爻的具体组合，则是大不相同的。

以三阳类的泰卦为例，它的三条阳爻可以有4种组合(0、1、2或3条可变阳爻结合相应的3、2、1或0条不可变阳爻)，它的三条阴爻也有4种组合(0、1、2或3条可变阴爻结合相应的3、2、1或0条不可变阴爻)。所以，构成泰卦的64种变化仅有4×4=16个独立概率。这16个独立概率适用于所有20个三阳类卦，这就是说，构成三阴类卦的1280种变化(64×20)里只有16个独立的概率。譬如，688997的泰卦甲和868799的泰卦乙，概率是相等的，是(1×72×32×5)/166=0.000131428，故概率为0.01314%。这是因为，两者都是由一条可变阴爻+两条不可变阴爻+两条可变阳爻+一条不可变阳爻来构成的。有同样概率的泰卦共有9种变化。三阳卦类有20个，所以共有1280种变化(64×20)的三阳类卦，概率合起来是0.015625×20=31.25%(见图7)。

图6

图7

我们也可以从另外一个角度切入，来计算和运用附录三的概率表。既然每个易卦都是两个三爻纯卦的叠加，另一个方法脉络更单纯、更易于理解，就是计算8个纯卦的概率，然后相乘而成为64卦(详见图8)。

图8

八卦可分四类：A零阳卦——地；B三阳卦——天；C一阳卦——雷、水、山；D二阳卦——泽、火、风。各卦的概率均为12.5%，也就是1/8。一阳、二阳类各有三个，所以一阳类、二阳类的概率，各为37.5%。四类的概率加总当然是100%。

据此不难明白，筮占获得一个易卦(所谓“起卦”)，可以有64种变化，其中独立的概率仅20个。用上文里举过的例子，泰卦甲688997和泰卦乙868799来验证。地天泰卦，甲的上体地卦688，乙的上体地卦868，都是三条阴爻，一条可变两条不可变，概率同为0.011962891；甲的下体天卦997，乙的下体天卦799，三条阳爻里也都是两条可变一条不可变，概率同样都是0.010986328。两者的乘积为0.000131428，同上面计算的结果是一样的。也就是说，泰卦甲和泰卦乙的概率都是0.01314%。

邵雍的“加一倍法”有4096种变化，即六十四个易卦，每卦各有64种变化。计算分析的结果表明，其独立的概率才84个。从附录三的概率表，我们很容易加总起来得出；在图8里也可以计算得到。八卦(三爻)的变化“加一倍”即二次方是64种，其独立的概率仅20种。那么两个八卦叠加之后，独立概率又是几何？也是84种。读者不妨排出一个20×20的矩阵，400个乘积归并之后，剩下的不同概率值(distinct values)，也正好是84个。

从实用的角度来讲，不必太过精确。于是六十四个易卦，得到每卦的概率为1.56%。其中零阳卦1个、一阳卦6个、二阳卦15个、三阳卦20个、四阳卦15个、五阴卦6个、六阳卦1个。这七个类别的概率，分别为1.56%、9.36%、23.4%、31.36%、23.4%、9.36%、1.56%。

通过辨析大衍筮法，得以知道蓍占的结果，阴爻和阳仪——可变及不可变——的不同组合的准确概率，从而了解占得一卦的各种变形的机会有多少，占得的卦又将作何变化，用易学术语来讲，是得到“之卦”的机会又是多少。在此“起卦”正确的基础上，才能够解卦，问凶吉、知得失，才有可能顺应“道”或“天意”，从而顺势利导地趋利避害。

附录一：三阶段决策树

注解：①“存体”(50茎蓍草里先取出1茎不用)；②“挂一”(再拿走1茎)后把“致用”的48茎蓍草分作两群(“分二”)；③按“扐”(“揲四”即以4茎为一簇)，取走核定的余数(“归奇”)。此第一变(I)，余下40茎的概率为四分之一，余下44茎的概率则为四分之三；④重复②、③成第二变(II)。“挂一”和“归奇”之后，分别剩下43茎或39茎。即剔除余数(3或7)后，从43茎剩下的是40茎或36茎，概率各半，从39茎剩下的是32茎或36茎，概率都是各半。再重复②③④成第三变(III)，则剩下24、36、28、32茎，概率分别为十六分之一、十六分之三、十六分之一(或三)、十六分之三(或一)。结果是，得到6、7、8、9(四的整除数)的概率，归并起来，分别为1/16、5/16、7/16和3/16。

附录二：易卦成卦概率表(大衍筮法引入可变和不可变爻后)

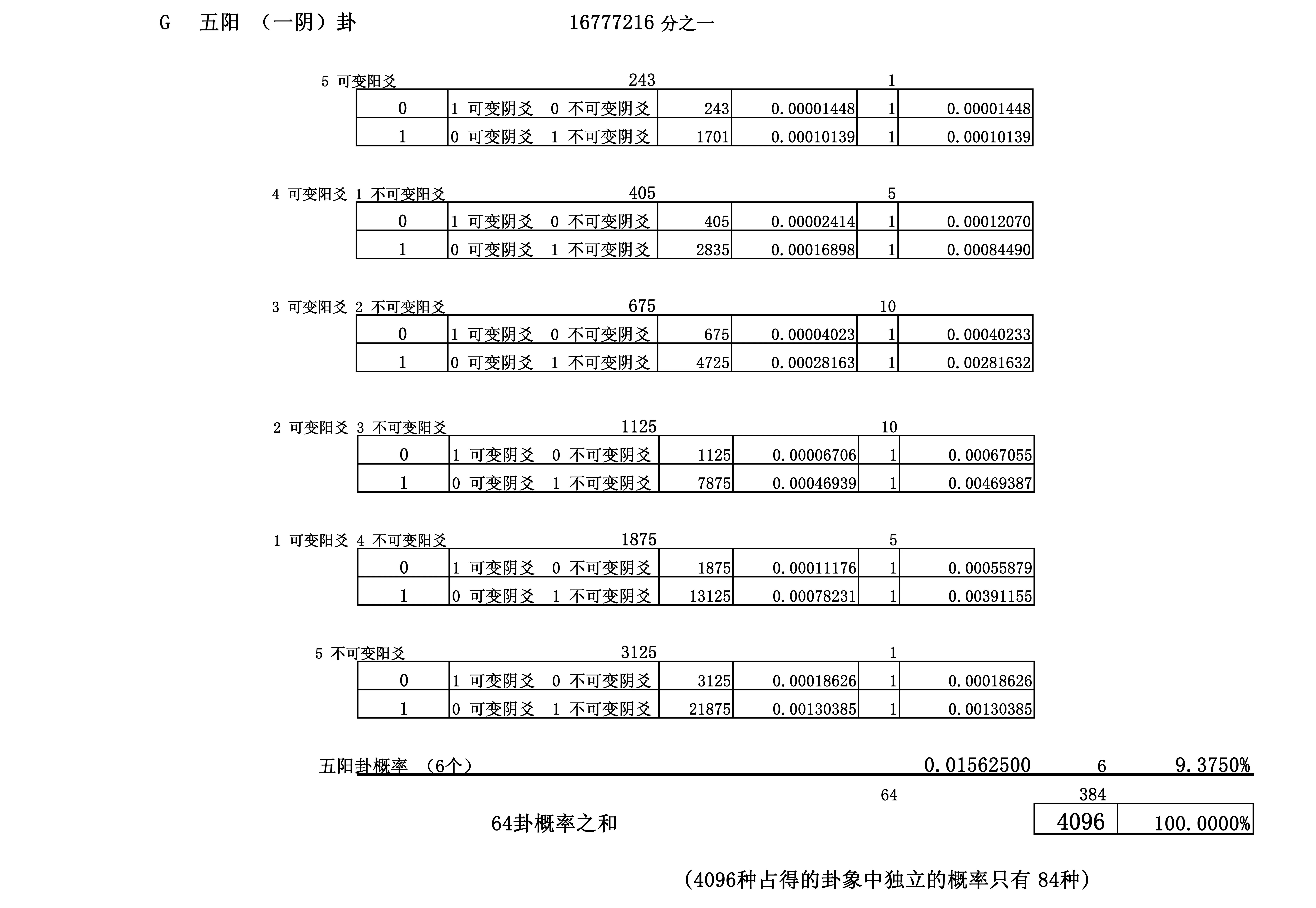
[责任编辑扬眉]