粗糙表面毫米波传播信道特性研究及图论建模

张超 尹学锋 余子明

(1. 同济大学电子与信息工程学院,上海 201804;2. 华为技术有限公司,成都 611731)

引 言

随着近些年来第五代移动通信研究和应用的深入,毫米波频段,即波长在厘米级或毫米级的无线电波频段的应用已经成为无线通信研究中的热门话题. 长期以来,毫米波频段因其具有丰富的频谱资源而受到军事和民用企业的广泛关注,多年来已经在通信、航空和遥感等领域[1-3]有着丰富的应用. 目前毫米波频段测试主要集中在28,39,60以及72 GHz频段. 由于工作波长较短,毫米波在传播过程中更容易受环境影响. 在低频波段,如频率小于或等于6 GHz,电磁波工作波长远大于物体表面粗糙程度,具有粗糙表面的散射体对电磁波传播影响很小[4]. 在毫米波频段,电磁波工作波长和散射体表面褶皱或者突起尺寸相当,电磁波在物体表面的主要传播机制由反射向散射过渡,整体传播信道特性会产生较大变化[5],因而对于构建能够真实体现毫米波电波传播特性的信道模型也提出了更高的要求.

许多文献已对粗糙表面对电磁波的散射和反射特性的影响进行了大量研究[6-12]. 文献[9-10]中研究了在中心频率为60 GHz情况下不同入射角度和粗糙程度对电磁波散射特性的影响,提出通过对基尔霍夫近似方法得到的参数进行设定来表示物体表面的粗糙程度. 文献[11]研究了在中心频率为35 GHz情况下,不同土壤表面粗糙程度和潮湿状态对电磁波的反射特性产生的影响,结论表明潮湿的土壤表面产生的电磁波散射在电磁波传播过程中占主导作用,干燥的土壤则是体散射中的主导因素. 文献[12]研究了26.5 GHz和40 GHz,入射角度从5°到70°情况下三种散射体对电磁波传播信道的影响,成果展示出物体的几何形状、波的极化和入射角度均对散射现象有较强的影响. 此外,当表面粗糙程度高时,散射变化对频率变化不是很敏感,水平极化波比垂直极化波更容易受到表面粗糙程度变化的影响. 目前针对粗糙表面对毫米波信道影响的研究主要针对对接收功率的影响,并没有对小尺度衰落提出更进一步的分析与建模,这也是本文在研究过程中试图解决的主要问题.

电磁波在物体有效粗糙表面产生的散射分布和相应的传播系数遵循基本的传播定理,如路径损耗定理、能量守恒定理和传输衰减定理. 图论正是基于这些传播定律,利用数字地图(用空间中分布的点来描述墙面、建筑等物体的实际形状)来计算电磁波在空间中传播的传输矩阵. 图论在计算以电磁波散射为主的传播路径时,有着很好的表现[13-14].

本文将两种相同尺寸不同表面粗糙度的物体放置在微波暗室中,通过测量接收通过物体表面传播回来的电磁波信号,分析了能够表示信道色散特征参数的统计特性,然后利用传播图论[15-16]对测试场景进行仿真,将仿真结果与实际测量结果进行比对,得到能够描述不同物体表面的粗糙系数,建立相对应的参数化图论仿真模型. 本文的分析和建模将为毫米波频段信道精确建模提供基础数据和模型.

本文主要内容如下,第一部分介绍了实验的测量环境、测试系统的重要参数,然后根据实测数据分析了功率时延谱、时延扩展等参数;第二部分利用图论进行仿真,将得到的功率时延谱与实际测量值进行对比,分析了两者的匹配情况,从而验证图论信道精确建模在毫米波频段的应用潜力.

1 实验测量

1.1 测量环境与系统

本文的测量环境选择在微波暗室中进行,微波暗室能够避免电磁波在传播过程中受到其他物体反射、散射而产生杂波影响,从而提高测量过程中的精准度. 测试系统包括可编程网络分析仪(Programmable Network Analyzer, PNA)、用来控制收发和存储数据的笔记本电脑、两个工作在50～75 GHz的喇叭天线、两个具有相同尺寸的粗糙表面和光滑表面(表面分别由具有不同粗糙程度的铝箔纸覆盖),以及高精度三维导轨. 电脑连接PNA控制信号的收发,实测场景图和系统框图如图1和图2所示. 发射端和接收端均采用增益为25 dB的喇叭天线,水平放置在微波暗室的一侧,被测物体放置在微波暗室三维高精度导轨上,由导轨控制被测表面产生微小移动. 两个天线高度和被测物体中心高度均为1 m,两个喇叭天线间距为1 m. 表1列出了测试系统的详细重要参数. 图3是两个不同粗糙表面详细对比图,粗糙度的评定常用轮廓算术平均差Ra来表示,数值越小,表明表面越光滑;数值越大,表明表面越粗糙[17]. 通过图3中对物体表面粗糙度的进一步量化可以计算出我们实验中采用的两种不同粗糙表面的粗糙度Ra,其具体数值在表1中列出.

图1 实测场景图

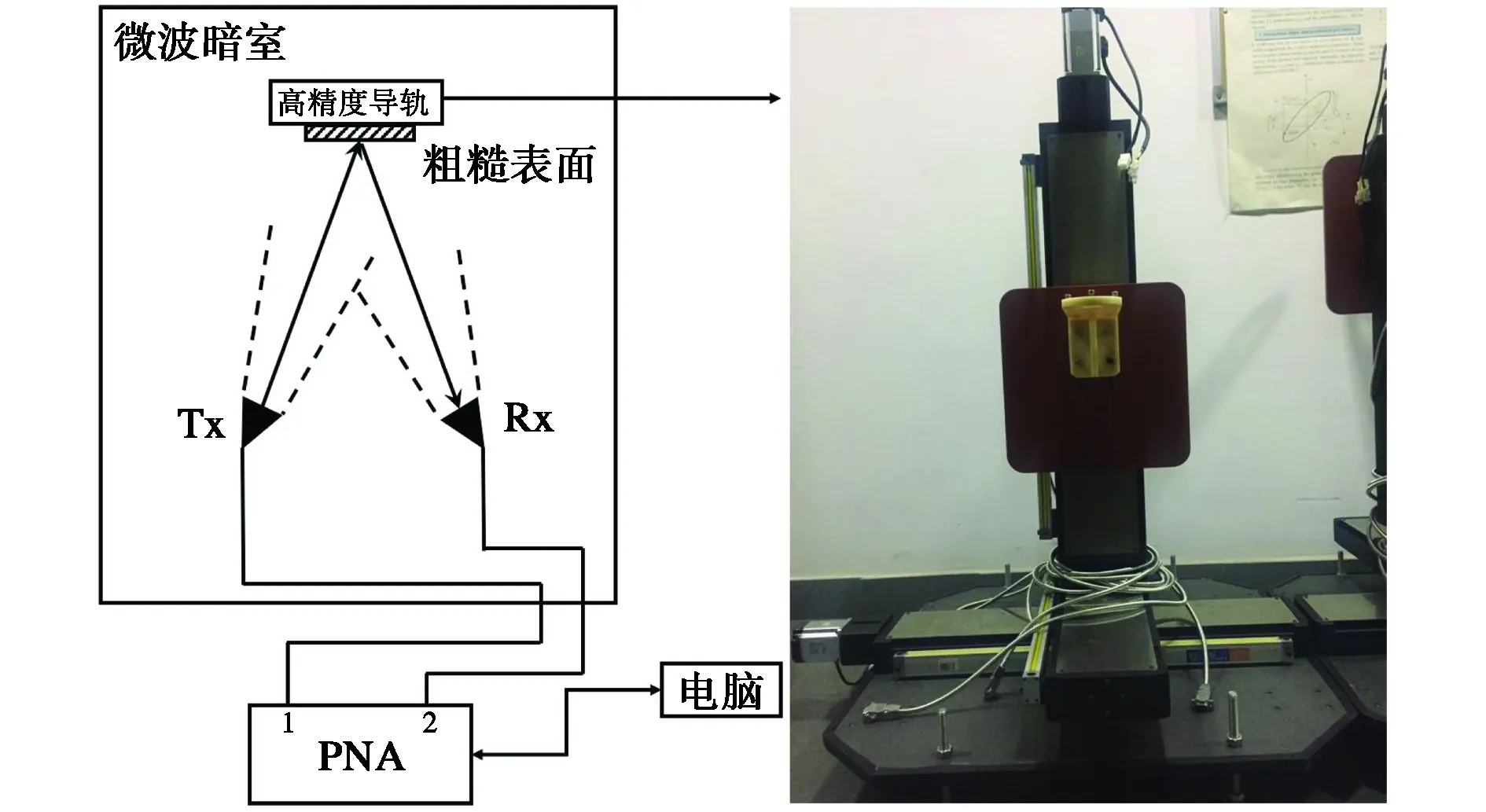
图2 系统框图和三维高精度导轨

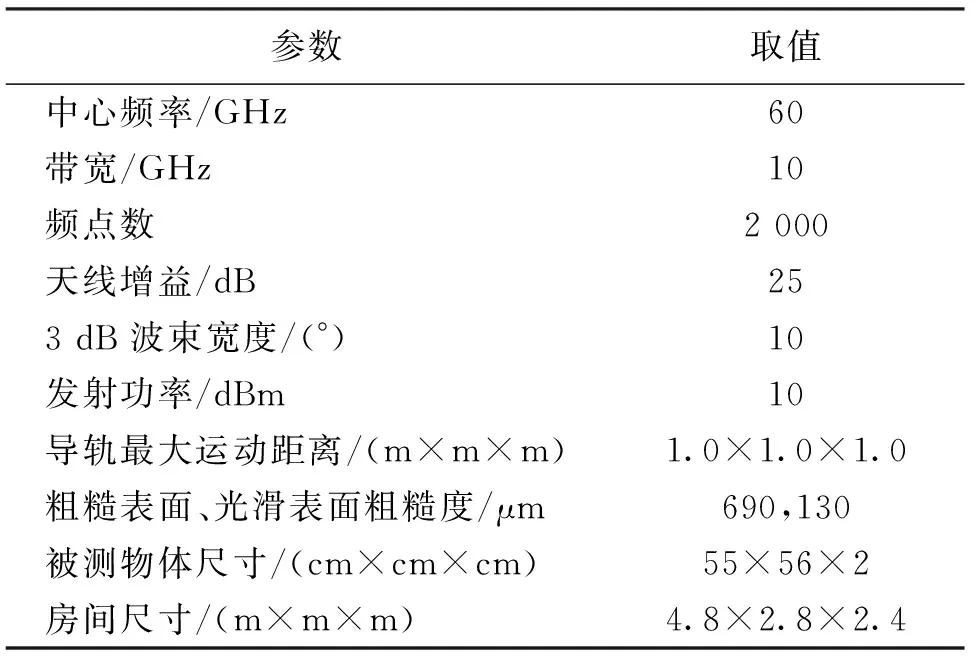
参数取值中心频率/GHz60带宽/GHz10频点数2000天线增益/dB253dB波束宽度/(°)10发射功率/dBm10导轨最大运动距离/(m×m×m)1.0×1.0×1.0粗糙表面、光滑表面粗糙度/μm690,130被测物体尺寸/(cm×cm×cm)55×56×2房间尺寸/(m×m×m)4.8×2.8×2.4

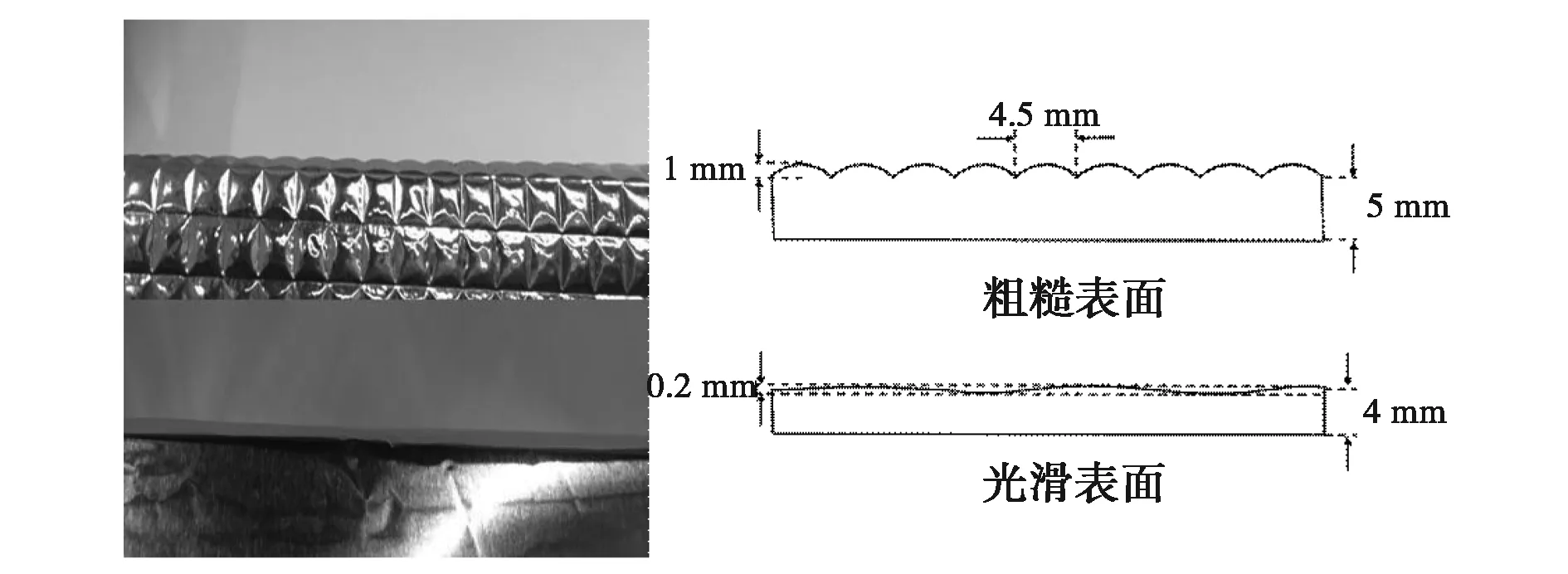
图3 两种不同粗糙度表面对比

文中测试中心频率为60 GHz,采用超宽带10 GHz,超宽带电磁波信号具有很强的空间分辨力,能够提高系统在时延域的多径分辨率(径向距离为3 cm). 目前超宽带的技术也在数据传输、定位、识别等方面有着较为广泛的应用,针对超带宽信道的研究和建模工作也有些积累[18]. 本研究中,中心频点电磁波的工作波长为5 mm,当电波照射到物体表面时,由于被测物体表面有不同程度的褶皱或者突起,并且尺寸与波长相当,将会对电磁波传播产生较大影响.

1.2 数据分析

1.2.1 功率时延谱

图4对比了根据两组测试数据得到的信号功率时延谱,其中蓝色实线代表电磁波经过粗糙表面的信号功率时延谱,红色虚线代表电磁波经过光滑表面的信号功率时延谱. 从图4可以看出:在峰值处蓝色实线的功率小于红色虚线,这表明电磁波在空间中从发射端经过粗糙表面再到接收端传播的路径损耗明显大于经过光滑表面的路径损耗;从衰落情况来看,经过粗糙表面的空间信道存在明显的多径现象,而光滑表面散射的信号能量平稳衰落,没有明显的多径叠加情况;两种情况下峰值时延均在18 ns左右,路径传播距离约5.4 m,与实际场景相符. 在18 ns处,电磁波经过粗糙表面后接收到的电磁波功率小于经过光滑表面接收到的电磁波功率. 此外,在时延18～19 ns处,电磁波在粗糙表面产生了明显的多径现象,此时电磁波由于多径叠加平均功率高于电磁波经过光滑表面接收到的电磁波功率. 在19 ns以后,红色虚线的功率略高于蓝色实线,两者逐渐衰落至噪声线,此时接收功率主要为电磁波经过物体表面的多次弹射后电磁波功率,这表明电磁波经过较为粗糙表面的多次弹射后接收到的信号功率小于经过光滑表面的信号功率.

图5将两次测量计算得到的归一化功率时延谱进行对比,可以看出,两者的接收信号衰落趋势非常相似. 以归一化功率从峰值衰落到0.5为例,两者均经过了4 ns左右. 同样,从图中可以看出电磁波经过粗糙表面存在明显的多径叠加现象.

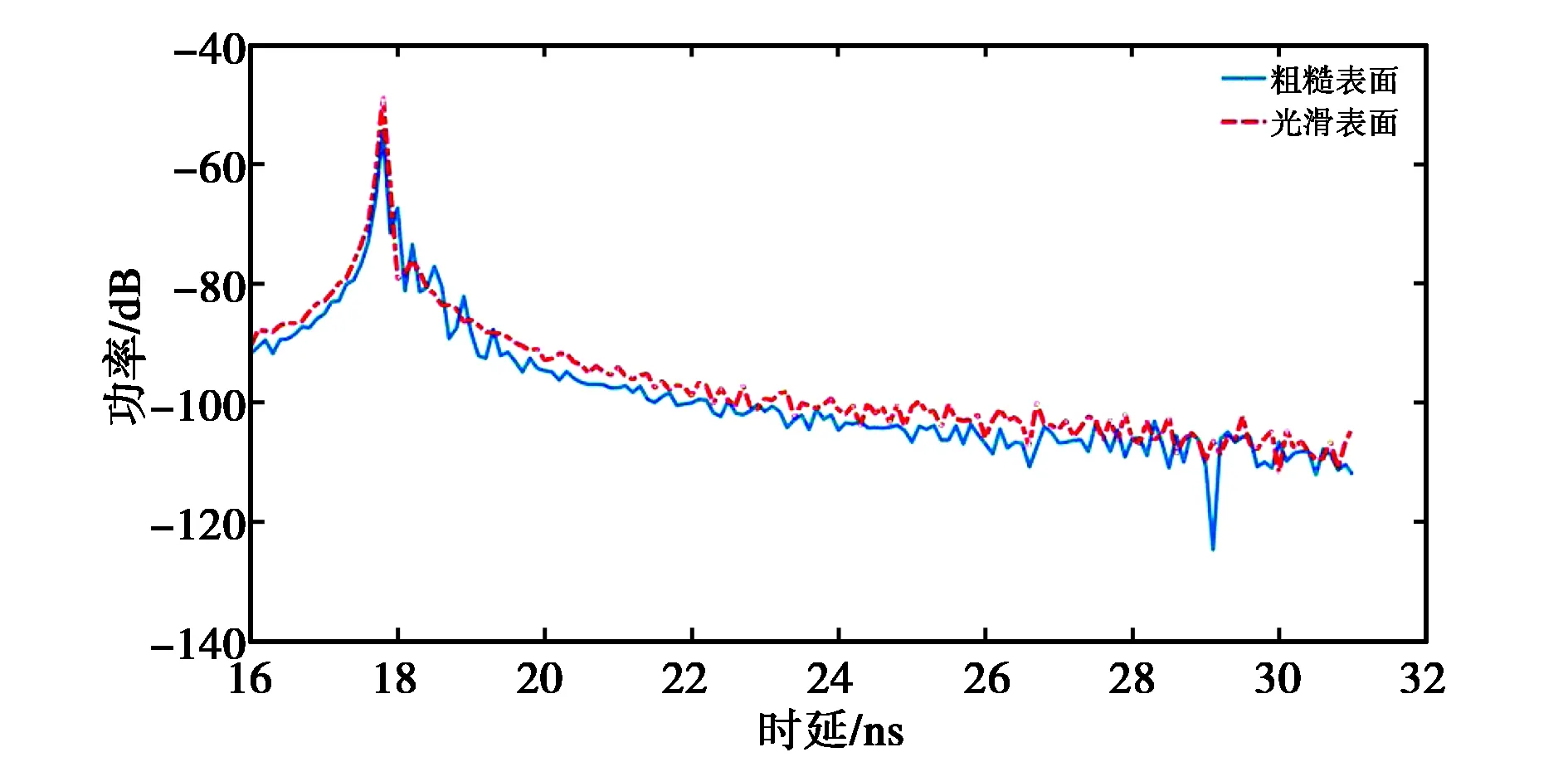
图4 实测功率时延谱

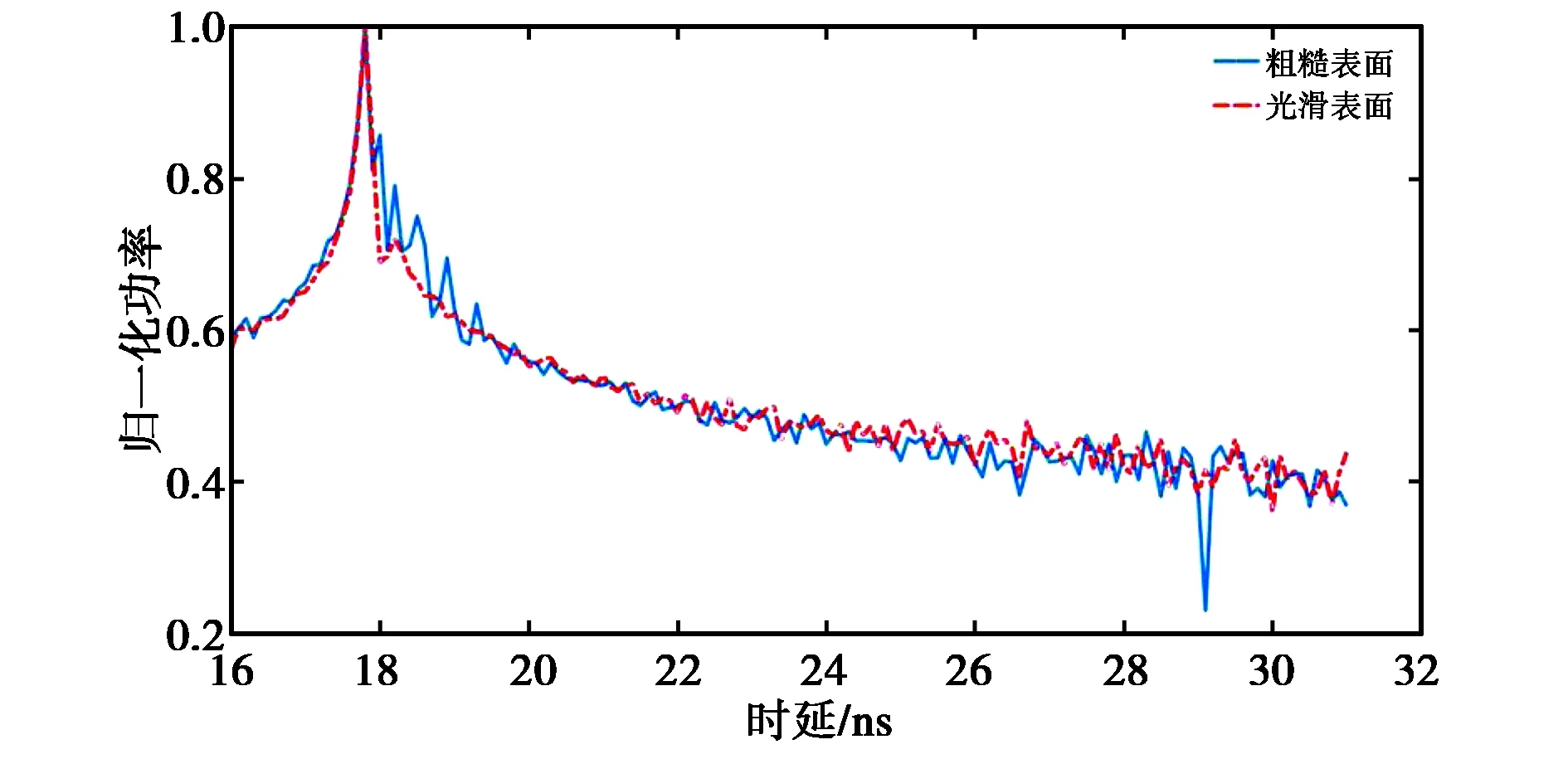
图5 归一化的实测功率时延谱

1.2.2 时延扩展

在无线通信系统中,时延扩展与电磁波传播环境密切相关,是多径信道时延特性的统计描述和无线信道仿真中非常重要的参数. 通常可以用平均时延和均方根时延来表示电波信号的时延特性. 计算方法如下:

假设我们得到信道响应为h(t,τ),一般情况下h(t,τ)可以表示为

(1)

式(1)可以简写为

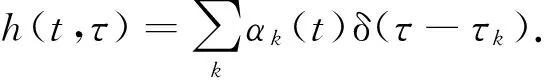
(2)

式中:αk(t)表示接收信号以复数表示的幅值;变量k代表第k条路径;τ表示信号在空间中传播产生的时延. 信号的瞬时功率时延谱P(t,τ)可以写为

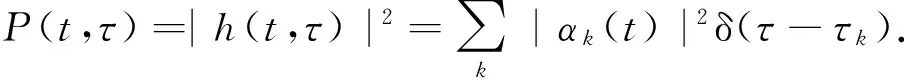
(3)

所要求得的平均时延τm和均方根时延τRMS可以计算为:

(4)

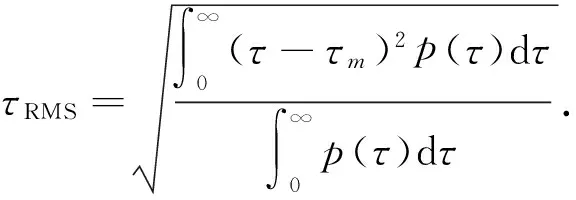
(5)

图6为根据两个被测物体的功率时延谱所求得的均方根时延扩展的累积概率分布,快拍数为200. 从动态范围来看,经过粗糙表面的空间信道的均方根时延扩展变化范围约为0.06～0.37 ns, 经过光滑表面的空间信道的均方根时延扩展变化范围约为0.01～0.27 ns;从分布情况来看,前者在均值处分布较为集中,后者在小于0.05 ns处有较为集中的分布,后面呈现类似均匀分布. 这可能是当物体表面比较粗糙时,电磁波经过由导轨等间隔移动产生的粗糙表面样本散射后获取的数据仍然存在一定的相关性,导致光滑表面的均方根时延扩展并没有呈现出预期的具有规则形状的概率分布,如正态、对数正态等;从整体来看,受粗糙表面影响的信道均方根时延扩展的均值明显大于受相对光滑的表面影响的信道.

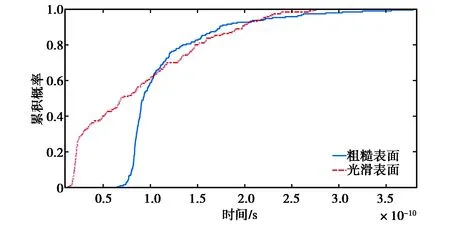
图6 均方根时延扩展的累积概率分布

2 建模仿真

利用图论信道建模是一种对电磁波传播有效的仿真方式,其性能已经在文献[13]中与射线追踪和实测数据进行对比,结果表明图论的仿真方式所得结果具有较高的可信度,可以用在室内和城市场景中进行毫米波信道仿真. 图7是图论理论模型的示例. 在图论建模中,信道传输函数H(f)可以写为

H(f) =D(f)+R(f)(I+B(f)+

B2(f)+…)T(f)

=D(f)+R(f)[I-B(f)]-1T(f).

(6)

式中:D(f)表示视距(Line-of-Sight, LOS)传输矩阵;T(f),R(f)和B(f)分别表示发射端到散射体,散射体到接收端,散射体到散射体的传输矩阵;I表示单位矩阵;Bn(f)表示从散射体到散射体第n次弹射的传输矩阵. 在本文测试中,没有LOS传输情况,因此传输矩阵D(f)为零矩阵. 一条路径的传输函数可以计算为

Ae(f)=ge(t)exp(-j2πτef+jφ).

(7)

Ae(f)可以用来分别计算传输矩阵D(f),T(f),R(f),B(f).式(7)中:τe是电波传播过程中产生的时延;φ是随机的相位旋转;ge(t)是计算传输矩阵时产生的能量衰减. 在反射、散射、绕射不同情况下,ge(t)计算方式也不同[14].在文献[13]中,作者详细推导了ge(t)的计算方式,表明ge(t)与物体表面散射系数和在生成数字地图时取点的疏密程度有关.

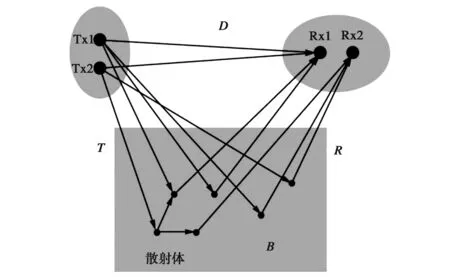
图7 图论传播模型示例[14]

图8是根据实际测量场景数据生成的图论仿真数字地图,被测物体用许多代表粗糙表面的点来表示(图8左上角为代表粗糙表面布点放大后的情况),绿色虚线表示电波在传播过程中经过单次弹射到达接收端的路径. 本次实验,我们在生成图论数字地图过程中,按照与粗糙物体实际表面颗粒密度相同的方式来计算,数字地图生成之后,就能通过式(6)和式(7)计算传输矩阵. 在本文中均采用图论经过四次弹射后仿真结果,文献[13]已经证明在弹射次数增加时,图论能够获得更好的仿真结果.

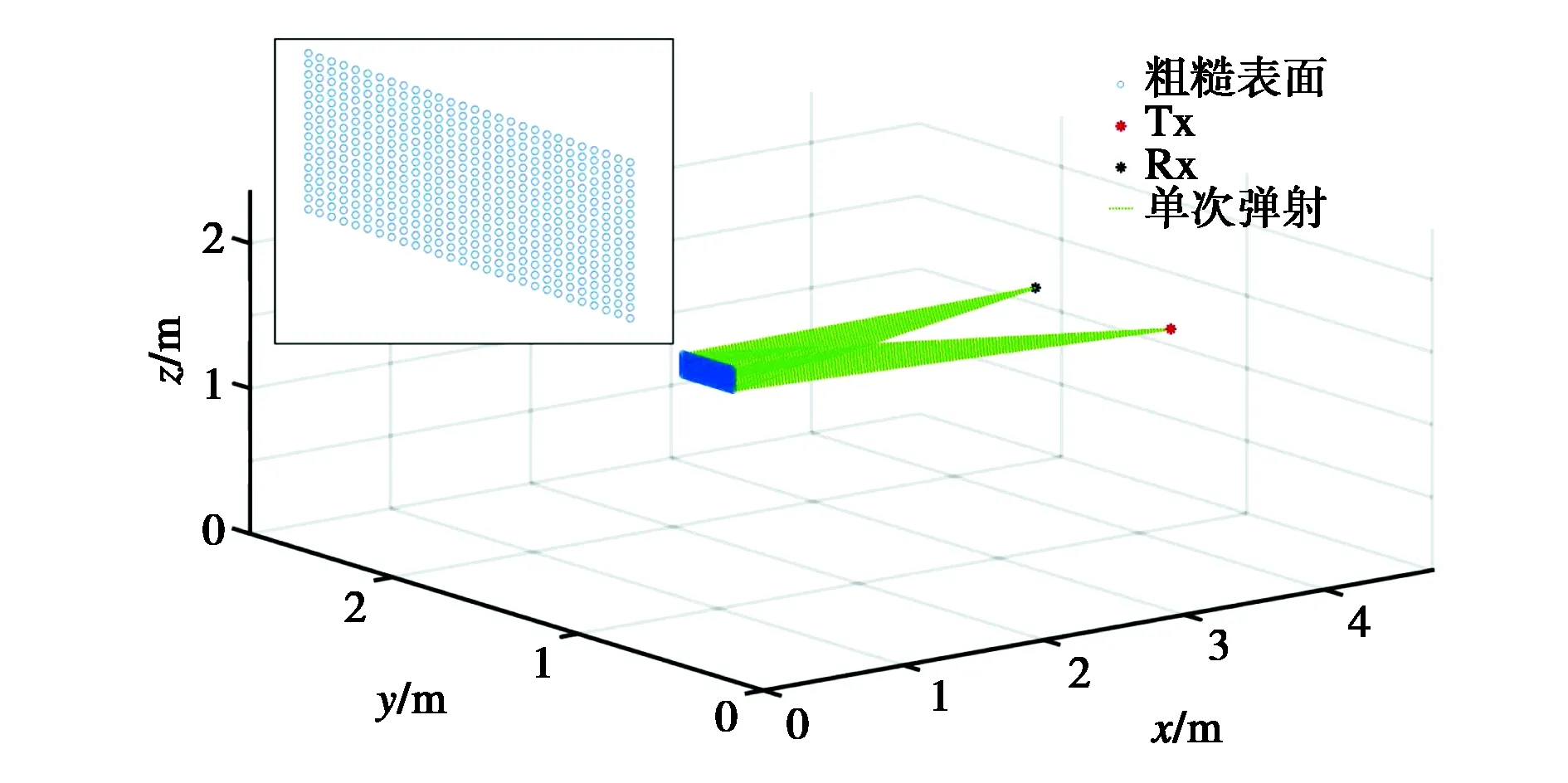
图8 基于实测数据图论仿真数字地图

图9将图论200次仿真结果与光滑表面的实测数据的功率时延谱进行对比,设置其中光滑表面散射系数s=0.05. 黑色实线表示实测电波经过光滑表面后接收到的信号;黑色虚线表示采用图论仿真得到接收信号. 从图9可以看出:和实测数据对比,仿真结果的信号强度衰落趋势基本一致,在峰值处功率非常接近,衰落过程中没有明显多径叠加现象;在1.9 ns以后,仿真信号能量衰减明显大于实测数据,总体来说两者具有较好的匹配程度.

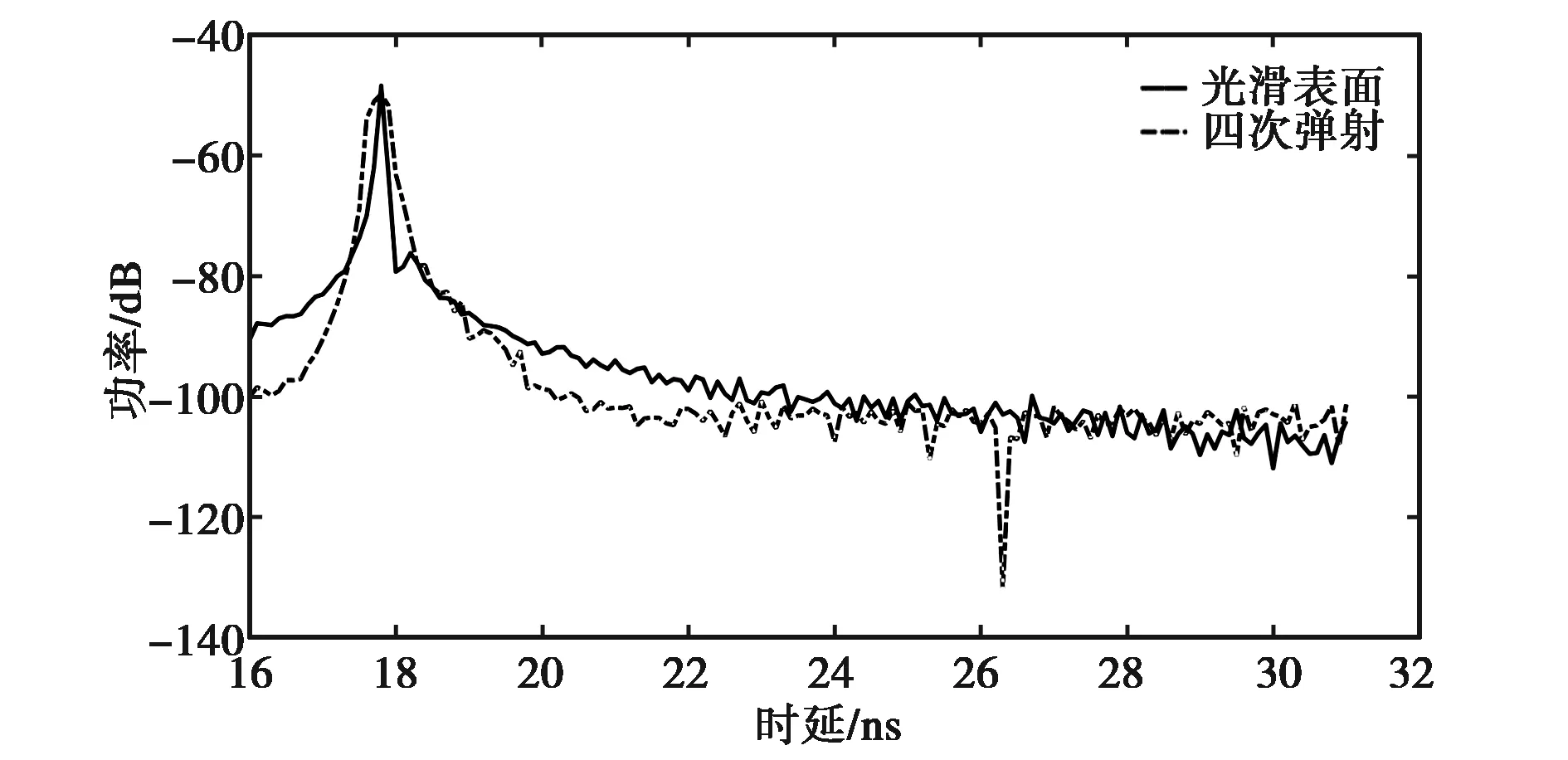
图9 图论仿真结果与光滑表面功率时延谱对比

图10将图论200次仿真结果和粗糙表面实测数据的功率时延谱进行对比,设置光滑表面散射系数s=0.5. 黑色实线表示实测电波经过光滑表面后接收到的信号;黑色虚线表示采用图论仿真得到的接收信号. 从图10可以看出:两者均有明显的多径现象,并且在峰值处时延和功率基本一致,图论仿真得到的信号能量衰落值小于实测数据信号能量衰落;经过时延2.2 ns后,两者基本都是处于噪声状态,和实际测量结果类似. 用图论的思想可以解释图4中实测数据对比结果,当物体表面散射系数较大时,存在明显的多径叠加,经过低阶次图论散射的路径仍然具有较高的能量,导致这段时间内,接收电磁波信号功率大于经过表面散射系数较小的物体. 经过高阶次图论散射的路径能量明显减少,此时经过表面散射系数较大的物体的接收功率小于散射系数较小的物体.

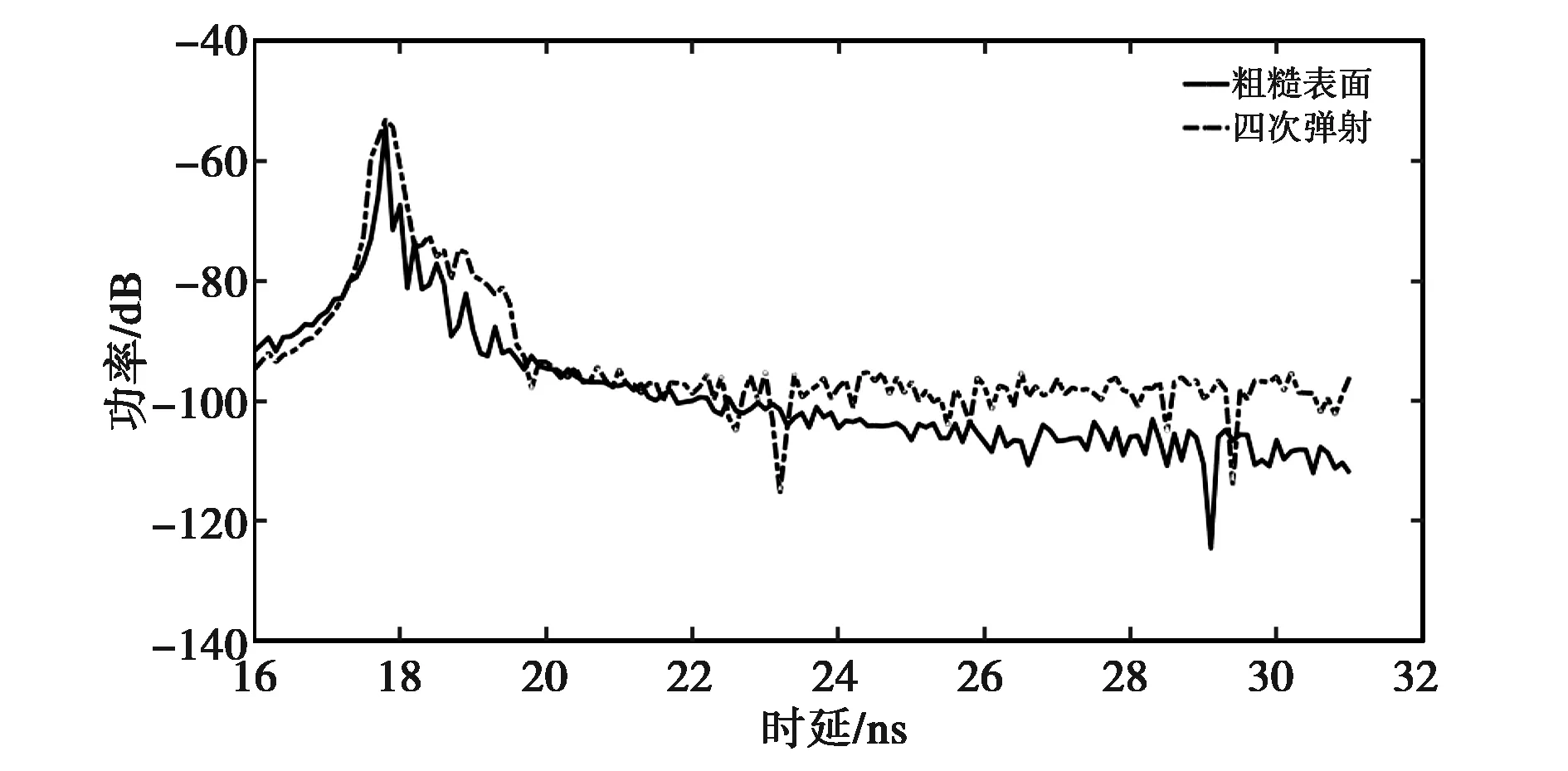
图10 图论仿真结果与粗糙表面功率时延谱对比

图11是将图论200次仿真结果分别计算接收信号的均方根时延扩展得到的累积概率分布. 黑色实线表示实测电波经过光滑表面后接收到信号的计算结果;黑色虚线表示实测电波经过粗糙表面后接收信号的计算结果.从变化范围来看,粗糙表面仿真

结果表明电磁波经过粗糙表面空间信道的均方根时延扩展变化范围约为0.07～0.2 ns,光滑表面仿真结果表明电磁波经过光滑表面空间信道的均方根时延扩展变化范围约为0.13～0.28 ns;从分布情况来看,两者呈现类似分布趋势;从均值来看,可以明显看出前者均值明显大于后者. 将仿真结果与实测数据结论对比可以看到,图论仿真中得到的粗糙表面和光滑表面的时延扩展范围均小于实际测量中的时延扩展范围,同时,仿真和实测结果均表明电磁波经过较为粗糙表面时产生的均方根时延扩展更大. 总体来说,用图论对粗糙物体表面建模能够较好地反映实际测量得到的粗糙表面信道特性.

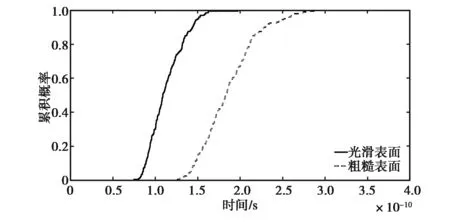
图11 图论仿真结果得到均方根时延扩展累积概率

3 结 论

本文针对不同粗糙程度表面对电磁波的传播特性影响进行了研究,分析了典型的信道参数的统计特性,结果表明电磁波经过物体不同粗糙表面后传播信道特性发生了改变,主要体现在电磁波功率和时延扩展. 在实验中采用超宽带和微波暗室场景进行测量,增加了实验结果的精确度,之后在实验数据的基础上采用图论信道建模方式进行了多次仿真,仿真结果和实测数据进行对比得到不同粗糙程度表面的散射系数,两者具有较好的匹配程度. 本文工作为以后高精度毫米波信道建模提供了参考依据.

[1] KING R W P. Lateral electromagnetic waves from a horizontal antenna for remote sensing in the ocean[J]. IEEE transactions on antennas & propagation, 2002, 37(10): 1250-1255.

[2] YIN X, CHEN J, TIAN M, et al. Personal authentication using the fingerprints of intra-body radio propagation channels[C]//International Symposium on Medical Information and Communication Technology. Tokyo, March 6, 2013:159-163.

[3] ZHAO X L, LIN W J. On effect of rough sea surface on the propagation of electromagnetic wave in atmospheric duct[C]//Sixth International Conference on Information Science and Technology. Dalian, May 6, 2016: 426-429.

[4] TRAN N, IMAI T, KITAO K, et al. A study on wall scattering characteristics based on ER model with point cloud data[C]//IEEE International Conference on Computational Electromagnetics. Kumamoto, March 8, 2017: 252-253.

[5] SALOUS S, ESPOSTI V D, FUSCHINI F, et al. Millimeter-wave propagation: characterization and modeling toward fifth-generation systems. [Wireless Corner][J]. IEEE antennas & propagation magazine, 2016, 58(6): 115-127.

[6] WANG G, ZHOU H, WANG Y, et al. Modeling surface roughness based on artificial neural network in mould polishing process[C]//IEEE International Conference on Mechatronics and Automation. Tianjin, August 3, 2014:799-804.

[7] NING Y, JIANG W. The electromagnetic characteristics of conducting rough surfaces at millimeter wave frequencies[C]//International Conference on Microwave and Millimeter Wave Technology. Nanjing, April 21, 2008:326-328.

[8] UCHIDA K, HASHIMOTO T, TAKEMATSU M, et al. Statistics of electromagnetic wave propagation along random rough surface[C]//International Conference on Network-Based Information Systems. Salerno, September 10, 2015:566-571.

[9] JUNG M W, KIM J H, YOON Y K, et al. Analysis of reflection and scattering characteristics at the 60 GHz frequency[C]//International Conference on Advanced Communication Technology. Pyeongchang, February 16, 2014:442-446.

[10] JUNG M W, KIM J H, LEE Y H, et al. Propagation prediction method for indoor communication system based on the surface roughness of clusters at the 60 GHz[C]//International Conference on Electromagnetics in Advanced Applications. Palm Beach, August 3, 2014:181-184.

[11] NASHASHIBI A, ULABY F T, SARABANDI K. Measurement and modeling of the millimeter-wave backscatter response of soil surfaces[J]. IEEE transactions on geoscience & remote sensing, 1996, 34(2):561-572.

[12] KIM Y H, YANG K S, KIM S H. Scattering characteristics of surface roughness in frequency and incident angle dependent at millimeter-wave[C]//1999 Asia Pacific Microwave Conference. Singapore, November 30, 1999, 3: 789-792.

[13] PEDERSEN T, STEINBOCK G, FLEURY B H. Modeling of outdoor-to-indoor radio channels via propagation graphs[C]//General Assembly and Scientific Symposium. Beijing, August 16, 2014:1-4.

[14] PEDERSEN T, STEINBOCK G, FLEURY B H. Modeling of reverberant radio channels using propagation graphs[J]. IEEE transactions on antennas & propagation, 2012, 60(12):5978-5988.

[15] TIAN L, DEGLI-ESPOSTI V, VITUCCI E M, et al. Semi-deterministic radio channel modeling based on graph theory and ray-tracing[J]. IEEE transactions on antennas & propagation, 2016, 64(6): 2475-2486.

[16] CHEN J, YIN X, TIAN L, et al. Millimeter-wave channel modeling based on a unified propagation graph theory[J]. IEEE communications letters, 2016, PP(99):1.

[17] 翟绪圣. 表面粗糙度测量[M]. 北京: 中国计量出版社, 1989: 12.

[18] 扈罗全, 朱洪波. 超宽带室内多径信道随机分析模型[J]. 电波科学学报, 2006, 21(4): 482-487.

HU L Q, ZHU H B. Stochastic calculus model for UWB indoor multipath channel[J].Chinese journal of radio science, 2006, 21(4):482-487. (in Chinese)