滴灌灌水小区水力设计的遗传算法研究

洪 涛，高焕芝，王新坤

（1. 镇江市工程勘测设计研究院，江苏 镇江 202003；2. 江苏大学流体机械工程技术研究中心，江苏 镇江 212013）

由于灌水小区内灌水器数量众多，计算工作量较大，微灌学者们一直在寻求准确、简单、便捷的设计方法。微灌灌水小区的设计大都是基于等距、等量出流假定，或将允许压力差在支管和毛管间进行分配，把灌水小区分成毛管和支管两个完全独立的单元，分别作为多孔出流管，采用多孔系数法[1]、能坡线法[2]、图解法[3]、有限元法[4-6]、遗传算法[7-8]等进行计算与设计。但是将支管、毛管作为两个独立单元的设计方法，破坏了灌水小区的完整性，计算方法存在一定的误差，而且很难应用于不等间距灌水器及双向坡地毛管的设计，也不能很好地满足微灌系统要求的平均灌水器流量和灌水均匀度，也有学者采用经验系数[9]、有限元[10-11]及毛管流量公式[5]将支、毛管联系为整体进行灌水小区的设计。本文将灌水小区作为一个整体进行优化设计，不再采用毛管和支管的等量、等距的出流假定，应用遗传算法理论与方法，提出一种方便、快捷的微灌灌水小区水力设计方法。

1 微灌灌水小区水力计算

以图1所示对支管节点、支管管段、毛管孔口和毛管管段进行编号，灌水小区上的支管节点压力、流量和毛管上各灌水器的流量、压力以及灌水器平均流量和灌水均匀度可按下列公式与步骤计算。

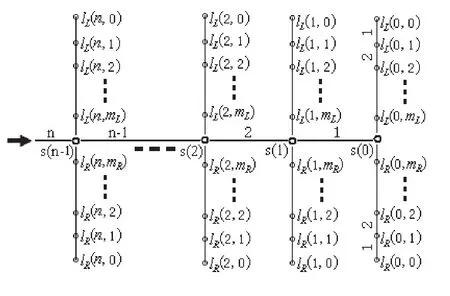
图1 灌水小区布置与编号示意图

Step1： 随机生成支管末端 s（0）节点压力水头Hs（0）：

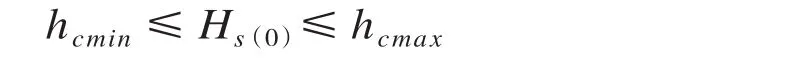
Step2： 应用二分法计算支管末端 s（0）节点处左侧毛管及灌水器的流量和压力：

（5）若 HlL（0）-HS（0）≤ε，则左侧毛管计算结束，转 Step3。否则，若 HlL（0）＞ HS（0），则 h''=hlL（0，0）；若 HlL（0）＜ HS（0），则 h'=hlL（0，0），重复（2） ～ （6）的步骤。

Step3： 应用 step2 的方法计算支管末端 s（0）节点处的右侧毛管及灌水器的流量和压力。

Step4： 支管 s（1）～s（n）节点的水力计算：

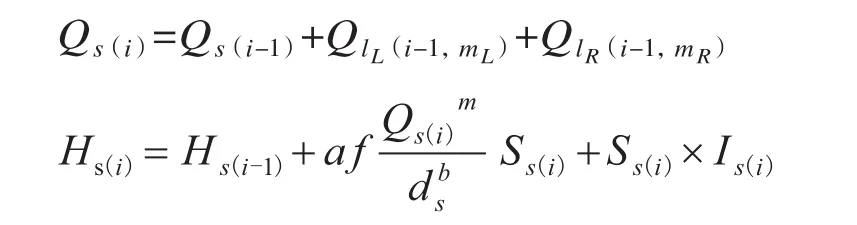
i =1，2，...，n，以 Hs（i）为支管第 i节点的压力水头，应用step2的方法计算支管第i节点处的左、右侧毛管流量和压力。同理进行第i+1节点的水力计算，直至计算出灌水小区进口水头Hs（n）。

Step5：

重复Step1～Step5，直q至qd，则计算结束。式中：

hlL（i，j）、hlR（i，j）—左、右侧毛管灌水器压力，m；

qlL（i，j）、qlR（i，j）—左、右侧毛管灌水器流量，L/h；

ΔhlL（i，j）、ΔhlR（i，j）—左、右侧毛管管段水头损失，m；

QlL（i，j）、QlR（i，j）—左、右侧毛管管段流量，L/h；

HlL（i）、HlR（i）—左、右侧毛管进口压力，m；

d1，ds—支管和毛管管径，mm；

Hs（i）—支管孔口压力，m；

Qs（i）—支管管段流量，L/h ；

Cu—设计灌水均匀系数；

a、f、m、b—水头损失计算系数；

SlL（i，j）、SlR（i，j）—左、右侧毛管管段长度，m ；

IlL（i，j）、IlR（i，j）—左、右侧毛管地形坡度；

Ss（i）—支管管段长度，m；

Is（i）—支管地形坡度；

ε—计算精度；

s（i）—支管节点编号；

lL（i，j）、lR（i，j）—左、右侧毛管灌水器编号；

mL、mR—左、右侧毛管灌水器个数。

上述计算过程中，只要知道支管末端s（0）节点处的压力水头Hs（0），通过逆递推就能完成灌水小区的水力计算，但要确定出使q=qd的Hs（0）的值，应用常规计算方法是难以完成的。本文借助遗传算法的高度并行及全局搜索能力，使得q逐步逼近qd，实现灌水小区的水力设计。

2 遗传算法模型

（1）构造适应度函数。根据上述灌水小区水力计算方法，可构造如下的目标函数：

式中：

qd—灌水器设计流量，L/h；

hcmin、hcmax—灌水器允许最大和最小工作水头，m。

将上述最小化的目标函转化为遗传算法所要求的最大化问题，构造出如下的适应度函数：

（2）编码。该遗传算法的优化变量为Hs（0）是一个连续的实数变量，采用实数编码方式。

（3）选择。随机从种群中选择2个个体，将好的个体选作父个体。

（4）交叉。对任意两个已配对好的父个体X1、X2，随机生成两个 [0，1]间的实数λ1、λ2，则λ1X1+（1-λ1）X2和λ2X1+（1-λ2）X2都具有父个体X1、X2的遗传基因，可以作为交叉后的子个体。

（5）变异。随机产生需要变异的个体和变量，在变量的可行域内随机产生新的值，替代原变量的值。

（6）算法实现。在 [Hs（0）]的可行域 [hcmin，hcmax]内随机生成一定规模初始群体作为第一代遗传群体，按照Step1～Step5的方法进行水力计算，由式（2）计算个体适应度，按照设计的选择、交叉、变异操作生成新一代群体，重复执行直到个体适应度的值满足精度要求为止。

3 实例计算

下面以均匀坡为算例进行模拟计算，计算的基本数据见表1。

对于上述实例的灌水小区计算问题，按图1所示对孔口及管段进行编号，应用上述遗传算法，取种群规模为30，最大遗传代数为15，进行模拟计算。由于毛管及灌水器数量非常多，所以只将支管的节点压力、流量及其它典型结果列于表2显示，其余详见图2和图3。

表1 基本数据

由表2可知，由于沿支管的地形坡度接近于平坡，而且支管的铺设长度短。因此，支管的最大压力出现在进口，其后压力降低，至末端降至最小。表2还表明，计算结果中每个支管节点处的支管压力和左、右侧毛管的进口压力基本相同，最大误差小于0.01%，左、右侧毛管进口流量之和与所在支管节点处的流量相同，计算所得灌水小区平均流量=2.2l/h，与qd完全相同，说明计算结果可靠、准确。

表2 灌水小区计算结果表

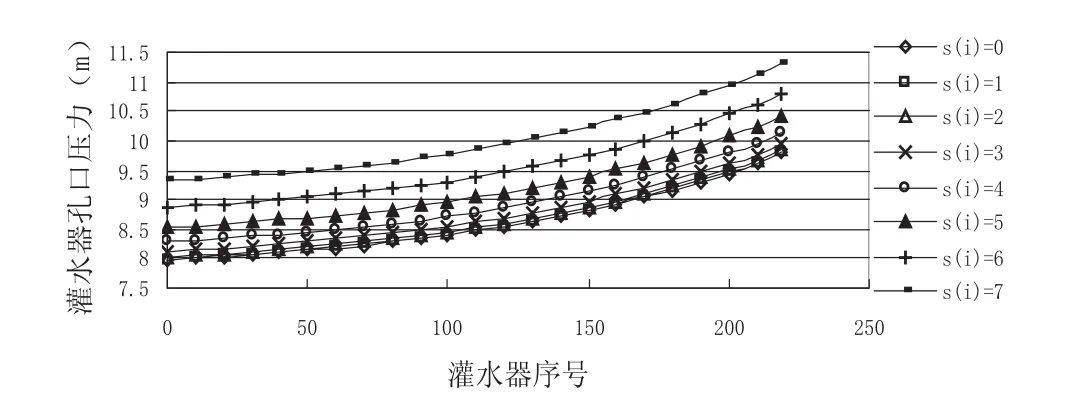
图2 左侧毛管灌水器压力曲线图

图3 右侧毛管灌水器压力曲线图

表2和图2、图3表明，左侧毛管最大压力均出现在毛管进口，最小压力出现在末端。右侧毛管的最大压力也都出现在毛管进口，最小压力都出现在第88孔口处，符合坡地毛管的水力特征。支管上有8个分流孔，每个分流孔左、右侧毛管上有480个灌水器，算法程序要计算近4000个节点处的流量和压力，在一台奔腾Dual 2.0GHz电脑上运行只需26 s，说明程序具有较好的求解效率。

考虑随机因素对算法求解性能评估的干扰，将算法程序独立运行100次，比较每次计算结果的灌水器平均流量与设计流量的相对偏差以及每次计算结果的毛管进口压力与最优解毛管进口压力的相对偏差，结果见表3。其中相对偏差小于0.01%的概率达到80%以上，小于0.5%的概率达到100%，说明算法计算结果稳定，具有较高计算精度和可靠性。

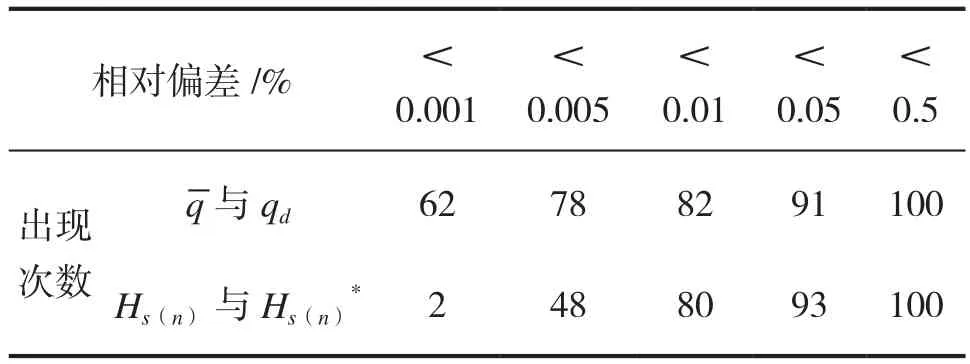
表3 计算结果与最优解相对偏差

4 结论与讨论

本文文中提出的遗传算法模型，不但能够进行灌水小区的水力设计，同时能够得到支管和毛管上每个节点的压力、流量和水头损失，以及灌水器平均流量、最大流量、最小流量等特征值及其孔口位置，确定压力偏差、流量偏差、灌水均匀度等灌水质量控制指标，便于微灌灌水小区水力特性的分析与研究，为灌水小区的管网布设及运行管理提供理论依据。算法程序只需要输入灌水小区水力设计要求的已知条件，就能自行运算出设计结果，具有很高的求解效率与计算精度以及良好的通用性和实用价值，可适用于非均匀坡、变管径、变间距坡地微灌灌水小区的水力计算与设计，也可用来对已设计或铺设好的灌水小区进行校核与评价。

[ 1 ]Christiansen JE. Irrigation by sprinkling[ M ] . California agriculture experiment station bulletin No. 670，University of California，USA，1942： 94 .

[ 2 ]I-pai Wu，Gitlin H.M. Design of drip irrigation lines with varying pipe sizes[ J ] . Journal of the Irrigation and Drainage Division，1977，103（4）：499-503 .

[ 3 ]李蔼铿.多口出流管道水力设计的微机诺谟图原理的研究 [ J ] . 水利学报，1994（2）： 1-8 .

[ 4 ]Bralts V F，Segerlind L J. Finite element analysis of drip irrigation submain units. Trans ASAE，1985，28（3）：809-814 .

[ 5 ]Kang Y H，Nishiyama S. Improved method for designing micro-irrigation submain units[ J ] . Irrigation Science，1997，17（4）： 183-193 .

[ 6 ]张志新，王建东，徐锁军，等. 虚拟节点有限元法解析滴灌毛管水力特性 [ J ] . 农业机械学报，2009，40（2）：68-70 .

[ 7 ]王新坤，蔡焕杰. 微灌毛管水力解析及优化设计的遗传算法研究 [ J ] . 农业机械学报，2005，36（8）：55-58 .

[ 8 ]王新坤，蔡焕杰 . 微灌坡地双向毛管最佳支管位置遗传算法优化设计 [ J ] . 农业工程学报，2007，23（2）：31-35 .

[ 9 ]张国祥，申亮 . 微灌灌水小区水力设计的经验系数法[ J ] .节水灌溉，2005（6）：20-23 .

[ 10 ]张志新，王建东，李鑫，等 . 虚拟节点有限元法解析滴灌支管水力学计算[ J ] . 农业机械学报，2009，40（3）：99-102 .

[ 11 ]郑纯辉，康跃虎，王丹 . 满足灌水器平均流量和灌水均匀度的微灌系统优化设计方法[ J ] . 干旱地区农业研究，2005，23（1）：28-33 .

[ 12 ]邱象玉，王福军 . 基于CAD的滴灌系统水力自动计算模型 [ J ] . 农业机械学报，2009，40（2）：54-57 .