变指标分数次Hardy算子的高阶交换子
2018-01-26于云凤
于云凤, 赵 凯
(青岛大学 数学与统计学院, 山东 青岛 266071)
变指数函数空间在流体力学和具有非标准增长条件的微分方程等领域应用广泛. 自Kov等[1]提出关于变指数Lebesgue空间和Sobelev空间后, 变指数函数空间得到广泛关注[2-4]. 目前, 调和分析中许多重要的算子在变指数函数空间中的有界性已得到证明. 例如: 文献[5-6]分别证明了分数次积分算子和分数次极大算子在变指数Lebesgue空间上的有界性; 陆善镇等[7]引入了经典的Herz-Morrey空间, 它是Lebesgue空间的推广, 也是Herz空间的延伸, 受变指数函数空间的影响; Izuki[8]引入了变指数Herz-Morrey空间, 研究了向量值次线性算子在其上的有界性, 并指出变指数Herz空间是变指数Herz-Morrey空间的特例; 此外, 文献[9-10]证明了变指数Herz空间上一些算子的有界性; 文献[11-13]研究了经典Herz-Morrey空间以及变指数Herz-Morrey空间上一些经典算子及其交换子的有界性. 另一方面, 自Hardy[14]证明了Hardy积分不等式后, 关于Hardy积分不等式和Hardy算子的研究已有很多结果[15-16]. 张璞等[17]研究了分数次Hardy算子在变指数Herz-Morrey空间上的有界性; 程星星等[18]得到了变指标分数次Hardy算子在变指数Herz-Morrey空间上的有界性.
由于分数次Hardy算子和分数次积分算子有许多共同特征, 因此, 研究变指标分数次Hardy算子与BMO函数生成的高阶交换子在变指数Herz-Morrey空间上的有界性有一定的理论意义. 本文主要研究变指标分数次Hardy算子与BMO函数生成的高阶交换子在变指数Herz-Morrey空间上的有界性.
1 预备知识
为方便, 首先给出变指数函数空间的概念.
定义1[1]设q(·):E→[1,∞)是可测函数, 变指数Lebesgue空间Lq(·)(E)定义为
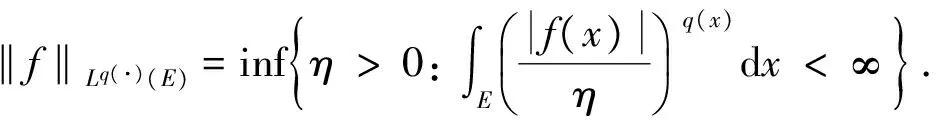

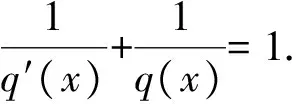
∀x,y∈n;

∀x∈n;

∀x∈n,
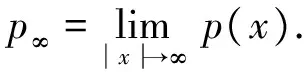
定义3[18]设f是n上的局部可积函数, 令β(x)是n上的可测函数, 满足0<β(x) 定义4设b∈BMO(n),β(x)如定义3.m∈, 变指标的n维分数次Hardy算子与b生成的高阶交换子定义为 下面给出变指数Herz-Morrey空间的定义. ∀k∈, 令Bk={x∈n: |x|>≤2k},Ak=BkBk-1, 用χk=χAk表示Ak上的特征函数. 定义5[8]设α∈, 0≤λ<∞, 0 其中 引理2[10]若q(·)∈B(n),m∈,i,j∈且i (1) ‖χR‖Lp(·)(n)~~, 引理4[18]令1<β-≤β(x)≤β+<∞,x∈B(0,r)B(0,r/2), 若β(x)在原点是log-Hölder连续的, 则 C-1rβ(0)≤rβ(x)≤Crβ(0), 0 若β(x)在无穷远处是log-Hölder连续的, 则 从装饰花纹上看,无论是工笔还是写意其表现出的题材都具有吉祥道喜之意。在这些纹样中一般表现的题材有花卉纹、山石、海水纹、鱼藻纹、回纹、卷线纹、龙、凤、麒麟纹、松、竹、梅纹、人物纹等。这些纹路一一反应出当时的社会文化。 C-1rβ∞≤rβ(x)≤Crβ∞,r≥1. 引理5[1]若p(·)∈P (n) , 则对所有的f∈Lp(·)(n),g∈Lp′(·)(n), 有 命题1[3]令q(·)∈P (n) , 若n), 则q(·)∈B(n). 定理1假设q1(·),q2(·),β(·)∈P (n),q1(x)≤q2(x), 0 其中当|x|>≥1时,β(*)=β∞, 否则β(*)=β(0). 对Ⅰ取Lq2(·)(n)范数, 由引理2以及命题6有 又 所以 由引理3知, 1) 若0≤j≤k, 由引理3得 2) 若j<0≤k, 则 3) 若j≤k<0, 则 从而由定义5知, 显然 故 证毕. [2] Cruz-Uribe D, Fiorenza A, Martell J M. The Boundedness of Classical Operators on VariableLpSpaces [J]. Ann Acad Sci Fenn Math, 2006, 31(1): 239-264. [3] Cruz-Uribe D, Fiorenza A, Neugebauer C J. The Maximal Function on VariableLpSpaces [J]. Ann Acad Sci Fenn Math, 2003, 28(1): 223-238. [4] Diening L, Harjulehto P, Hästö P, et al. Lebesgue and Sobolev Spaces with Variable Exponents [M]. Heidelberg: Springer-Verlag, 2011. [5] Diening L. Riesz Potential and Sobolev Embeddings on Generalized Lebesgue and Sobolev SpacesLp(·)andWk,p(·)[J]. Math Nachr, 2004, 268(1): 31-43. [6] Capone C, Cruz-Uribe D, Fiorenza A. The Fractional Maximal Operator and Fractional Intergrals on VariableLpSpaces [J]. Rev Mat Iber, 2007, 23(3): 743-770. [7] LU Shanzhen, XU Lifang. Boundedness of Rough Singular Integral Operators on the Homogeneous Morrey-Herz Spaces [J]. Hokkaido Math J, 2005, 34(2): 299-314. [8] Izuki M. Boundedness of Vector-Valued Sublinear Operators on Herz-Morrey Spaces with Variable Exponent [J]. Math Sci Res J, 2009, 13(10): 243-253. [9] Almeida A, Drihem D. Maximal, Potential and Singular Type Operators on Herz Spaces with Variable Exponents [J]. J Math Anal Appl, 2012, 394(2): 781-795. [10] Izuki M. Boundedness of Commutators on Herz Spaces with Variable Exponent [J]. Rendiconti del Circolo Matematico di Palermo, 2010, 59(2): 199-213. [11] Izuki M. Fractional Integrals on Herz-Morrey Spaces with Variable Exponent [J]. Hiroshima Math J, 2010, 40(3): 343-355. [12] WU Jianglong. Boundedness for Commutators of Fractional Integrals on Herz-Morrey Spaces with Variable Exponent [J]. Kyoto J Math, 2014, 54(3): 483-495. [13] 赵凯, 王永刚, 王磊. 非双倍测度下分数次极大算子交换子在Morrey-Herz空间上的有界性 [J]. 吉林大学学报(理学版), 2011, 49(5): 835-838. (ZHAO Kai, WANG Yonggang, WANG Lei. Boundedness of Commutators of Fractional Maximal Operators on Morrey-Herz Spaces with Non-doubling Measure [J]. Journal of Jilin University (Science Edition), 2011, 49(5): 835-838.) [14] Hardy G H. Note on a Theorem of Hilbert [J]. Math Z, 1920, 6(3/4): 314-317. [15] Andersen K F, Muckenhoupt B. Weighted Weak Type Hardy Inequalities with Applications to Hilbert Transforms and Maximal Functions [J]. Studia Math, 1982, 72(1): 9-26. [16] Golubov B I. Boundedness of the Hardy and the Hardy-Littlewood Operators in the Spaces ReH1and BMO [J]. Sbornik Math, 1997, 188(7): 93-106. [17] 张璞, 武江龙. 分数次Hardy算子在变指数Herz-Morrey空间中的有界性 [J]. 数学的实践与认识, 2013, 43(7): 247-254. (ZHANG Pu, WU Jianglong. Boundedness of Fractional Hardy Type Operators on Herz-Morrey Spaces with Variable Exponent [J]. Mathematics in Practice and Theory, 2013, 43(7): 247-254.) [18] CHENG Xingxing, SHU Lisheng. Boundedness for Some Hardy Type Operators on Herz-Morrey Spaces with Variable Exponent [J]. Journal of Anhui Normal University (Natural Science), 2015, 38(1): 19-24.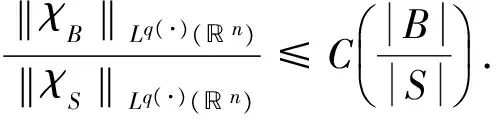

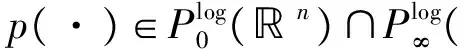

2 主要结果


