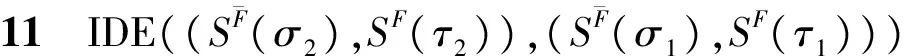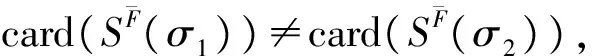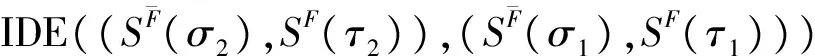函数P(σ,τ)-集合及其特征
2018-01-26于秀清徐凤生
于秀清, 徐凤生, 冀 娜
(1. 德州学院 数学科学学院, 山东 德州 253023; 2. 北京交通大学威海校区, 山东 威海 264401;3. 山东财经大学 MBA学院, 济南 250014)
0 引 言

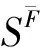
约定1有限函数论域U(x)与函数集合S(x)分别简记为U,S,
S={s(x)i|i=1,2,…,q}⊂U,
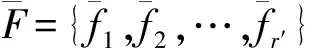

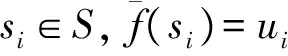


1 函数P(σ,τ)-集合
定义1[7]设函数集合S={s1,s2,…,sq}⊂U,α={α1,α2,…,αk}⊂V是S的属性集合.
如果αF满足
|βi∈V,βi∈α,f∈F},
(1)

(2)

(3)
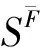
(4)


(5)
则称A(SF)是函数外P-集合SF的副集, 简称A(SF)是函数外副集, 且
A(SF)={ui|ui∈U,uiS, 0<χf(ui)<1,f∈F};
(6)
称Aτ(SF)是函数外P-集合SF的τ-副集, 简称Aτ(SF)是函数外τ-副集, 且
Aτ(SF)={ui|ui∈U,uiS,τ≤χf(ui)<1,f∈F};
(7)
称SF(τ)是S生成的函数外P(τ)-集合, 且
SF(τ)=SF∪Aτ(SF).
(8)



(9)
由约定1可知: 式(2)的等价表示为
(10)
式(6)的等价表示为
即函数外副集A(SF)是由所有被部分迁入S的函数组成的集合; 式(7)为uiS迁入S的部分设定了一个阈值τ(uiS被迁入S的部分越大, 特征函数值χf(ui)越大), 即Aτ(SF)是由迁移函数特征值χf(ui)在(τ,1)内函数构成的集合, 式(8)可写成
(11)
综上可得:


3) 对∀τ∈(0,1), 有Aτ(SF)⊆A(SF)与S⊆SF⊆SF(τ)成立;

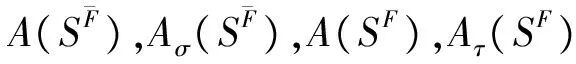
(12)





(13)
定理2的证明与定理1类似, 故略.
推论1设A(SF)是函数外P-集合SF的副集,SF(τ)是函数外P(τ)-集合, 则有
(14)


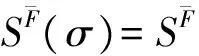




2 函数P(σ,τ)-集合的动态特征
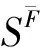
定义5若SF(τ)是函数集合S生成的函数外P(τ)-集合, 则实数λ(τ)即为SF(τ)相对于S的外包度, 简称SF(τ)的τ-外包度, 且
λ(τ)=card(SF(τ))/card(S).
定义6由κ(σ)与λ(τ)构成的实数对称为函数P(σ,τ)-集合相对于函数集合S的包度, 简称(σ,τ)-包度, 记为(κ(σ),λ(τ)).
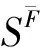

命题2对∀τ∈(0,1),有λ(τ)∈[1,card(U)/card(S)]; 且当F=Ø时,λ(τ)=1; 当SF(τ)=U时,λ(τ)最大,λ(τ)=card(U)/card(S).



(15)
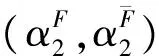

证明: 由定义2与定义3直接可得.
推论6在定理4的条件下, 有
(κ1(σ),λ1(τ))(κ2(σ),λ2(τ)),
(16)
其中(κ1(σ),λ1(τ))(κ2(σ),λ2(τ))表示κ1(σ)≥κ2(σ)与λ1(τ)≤λ2(τ)同时成立.


(17)
λn(τ)≤λn-1(τ)≤…≤λ2(τ)≤λ1(τ),
(18)



2) (κ1(σ),λ1(τ))(κ2(σ),λ2(τ))…(κn(σ),λn(τ)).


2) (κ(σ1),λ(τ1))(κ(σ2),λ(τ2)).


由结论1)知
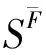
成立, 再根据定义4和定义5可知结论2)成立.
推论9设SF(τi)(i=1,2,…,n)是函数外P(τ)-集合, 如果0<τ1<τ2<…<τn<1, 则:
1)SF(τn)⊆SF(τn-1)⊆…⊆SF(τ1);
2)λ(τn)≤λ(τn-1)≤…≤λ(τ1).


2) (κ(σ1),λ(τ1))(κ(σ2),λ(τ2))…(κ(σn),λ(τn)).
3 函数P(σ,τ)-集合的辨识特征

这里I表示指标集合.
证明: 由推论10可直接得出.

(19)

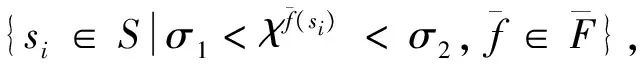

定理8设SF(τ1),SF(τ2)是函数内P(τ)-集合, 若0<τ1<τ2<1, 且UNI(SF(τ1),SF(τ2)), 则对∀τ*∈[τ1,τ2], 都有UNI(SF(τ1),SF(τ*),SF(τ2)).
证明: 与定理7的证明类似, 故略.
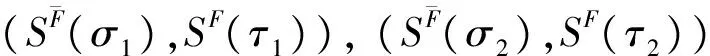
(20)

(21)
或者
(22)
成立. 如果令σ1<σ* 定理10设SF(τ1),SF(τ2)是函数内P(τ)-集合, 若IDE(SF(τ1),SF(τ2)), 则在τ1与τ2之间至少存在一点τ*, 使得 UNI(SF(τ1),SF(τ*)), IDE(SF(τ*),SF(τ2)), (23) 或者 IDE(SF(τ1),SF(τ*)), UNI(SF(τ*),SF(τ2)). (24) 证明: 与定理9的证明类似, 故略. 则在σ1与σ2之间至少存在一点σ*, 在τ1与τ2之间至少存在一点τ*, 使得 (25) 或者 (26) (27) 证明: 与定理11的证明类似, 故略. [1] SHI Kaiquan. Function P-Sets [J]. International Journal of Machine Learning and Cybernetics, 2011, 2(4): 281-288. [2] 林蓉, 史开泉. 函数P-集合与信息规律的属性控制 [J]. 计算机科学, 2012, 39(7): 225-228. (LIN Rong, SHI Kaiquan. Function P-Sets and Attribute Control of Information Laws [J]. Computer Science, 2012, 39(7): 225-228.) [3] 史开泉. P-信息规律智能融合与软信息图像智能生成 [J]. 山东大学学报(理学版), 2014, 49(4): 1-17. (SHI Kaiquan. P-Information Law Intelligent Fusion and Soft Information Image Intelligent Generation [J]. Journal of Shandong University (Natural Science), 2014, 49(4): 1-17.) [4] LIN Rong, FAN Chengxian. P-Sets and Identification of Inward Convergence [J]. International Journal of Convergence Information Technology, 2012, 7(7): 157-164. [5] 林蓉, 范成贤. 函数P-集合与信息规律动态特征 [J]. 山东大学学报(理学版), 2012, 47(1): 121-126. (LIN Rong, FAN Chengxian. Function P-Sets and Dynamic Characteristics of Information Regularity [J]. Journal of Shandong University (Natural Science), 2012, 47(1): 121-126.) [6] 赵树理, 张环理, 史开泉. 函数P-集合与内P-信息规律依赖内-挖掘 [J]. 计算机科学, 2013, 40(5): 237-241. (ZHAO Shuli, ZHANG Huanli, SHI Kaiquan. Function P-Sets and Internal-Mining of Internal P-Information Law Dependence [J]. Computer Science, 2013, 40(5): 237-241.) [7] 于秀清, 徐凤生, 孔淑霞. 函数内P(σ)-集合及其规律的动态特征 [J]. 吉林大学学报(理学版), 2015, 53(3):439-443. (YU Xiuqing, XU Fengsheng, KONG Shuxia. Function Internal P(σ)-set and Its Law Dynamic Characteristics [J]. Journal of Jilin University (Science Edition), 2015, 53(3): 439-443.) [8] 于秀清. P(ρ,σ)-集合与它的随机特性 [J]. 计算机科学, 2010, 37(9): 218-221. (YU Xiuqing. P(ρ,σ)-Sets and Its Random Characteristics [J]. Computer Science, 2010, 37(9): 218-221.) [9] 于秀清. P-集合的(σ,τ)-扩展模型与其性质 [J]. 山东大学学报(理学版), 2014, 49(4): 90-94. (YU Xiuqing. (σ,τ)-Expansion Model of P-Sets and Its Properties [J]. Journal of Shandong University (Natural Science), 2014, 49(4): 90-94.) [10] 于秀清, 董化玲, 徐凤生. 内P-集合副集的σ-生成和σ-强生成 [J]. 吉林大学学报(理学版), 2013, 51(4): 599-602. (YU Xiuqing, DONG Hualing, XU Fengsheng.σ-Generation andσ-Strong Generation of Assistant Set of Internal P-Set [J]. Journal of Jilin University (Science Edition), 2013, 51(4): 599-602.)