An Adaptive Strategy via Reinforcement Learning for the Prisoner’s Dilemma Game

Lei Xue,Changyin Sun,,Donald Wunsch,,Yingjiang Zhou,and Fang Yu

I.INTRODUCTION

G AME theory has become the natural mathematical method to discuss strategic and social interactions,particularly in a competitive environment[1].The prisoner’sdilemma,which exists in many areas,serves as a useful tool for studying human behavior in various social settings and has contributed insights to engineering science,economics,game theory,the analysis of social network structures,and psychology[2].The iterated prisoner’s dilemma(IPD)is a widely used model for analyzing the individual behavior of an agent within a given system.In the IPD,mutual cooperation could provide the highest total income,although selfish individual reasoning often leads to other choices.There are many examples of the Prisoner’s dilemma in real life,when people have to choose between being selfish or altruistic.Therefore,the famous computer tournaments for IPD were held by Robert Axelrod[3].He invited game theorists to submit strategies for playing IPD.The highest payoff was earned by the strategy named “tit-for-tat”,it is a strategy which cooperates in the first round and repeats what the opponent has done in the previous move.Some impressive results were collected in[3],the relevant message for people facing a prisoner’s dilemma can be summarized as follows:

1)don’t be envious;

2)don’t be the first to defect;

3)reciprocate both cooperation and defection;

4)don’t be too clever.

For one-shot prisoner’s dilemma,there is no doubt that betrayal will earn the best payoff for the agent.However,it is seldom that people just face between being selfish or altruistic only once.Thereafter,scholars turned their attention to seek the mutual cooperation during IPD.The spatial evolutionary game demonstrated that local interactions within a spatial structure can maintain cooperative behavior[4].Reference[4]dealt with the relative merits of various strategies when players who recognized each other meet repeatedly.This spatial version of the prisoner’s dilemma can generate chaotically changing spatial patterns.Reference[5]introduced a measure for the cluster shape and demonstrated that the macroscopic patterns can be used to determine the characteristics of the underlying microscopic interactions.Reference[6]studied the competition and strategy selections between a class of generalized strategies.

With the development of evolutionary computation,many scholars have made significant contributions to the research of IPD[7].Different agents within IPD games may utilize different strategies.Scholars have introduced numerous technologies which can be used to identify or modify IPD strategies.Some strategies are fixed and can be implemented using the finite state machine or Markov decision process[8].Other strategies are adaptive based on different representation schemes[9],[10].In order to determine which kind of strategy has a better performance under specific conditions,some studies have investigated using fingerprint and agent case embedding to analyze them[11]−[13].The existing research results also indicated that evolutionary strategies can compete well against some of the fixed strategies[14],[15].Inspired by these outstanding results,we propose an adaptive strategy based on temporal difference learning method which can consider both the achievement of mutual cooperation and better performance.

The reinforcement learning paradigm can be applied to solve many practical problems[16],[17].References[18]−[20]applied reinforcement learning method to solve nonlinear system problems.Moreover,learning to predict involves using past experience with an incompletely known system to predict its future behavior,and this type of learning is significant for the IPD.Reinforcement learning is an effective way to teach the agent how to make a decision based on the previous experiences.Reference[20]brought together cooperative control,reinforcement learning,and game theory to present a multi-agent formulation for the online solution of the team games.In[21],the scholars explored interactions in a coevolving population of model-based adaptive agents and fixed non-adaptive agents,and identified that the reinforcement learning method can serve as a useful tool for developing an adaptive strategy.Hingston and Kendall also incorporated reputation as the mechanism for evolving into the existing co-evolutionary learning model for IPD games,where the mechanism for evolving cooperative behaviors is reputation[22].Reference[23]designed a team of agents which can accomplish consensus over a common value according to cooperative game theory approach.Reference[24],[25]investigated the evolution of cooperation in the prisoner’s dilemma when individuals change their strategies subject to performance evaluation of their neighbors over variable time horizons.The main contribution of this paper is shown as follows:

1)A temporal difference(TD)learning method is applied to design an adaptive strategy.The feature of adaptive strategy is that it can balance the short-term rational decision for self interest against the long-term decision for overall interest.The evolutionary stability of the adaptive strategy is studied.

2)Three kinds of tournaments based on different complex networks are provided.During the tournaments in square lattice network which contains different strategies, the adaptive strategy earns a better payoff.As to the scale-free network constituted by adaptive agent,all the agents will cooperate with each other for long-term reward.

Therefore,the simulation results verify that the adaptive strategy is willing to choose cooperation without losing competitiveness.

This paper is organized as follows.In Section II,IPD is introduced.In Section III,TD(λ)method for prisoner’s dilemma is presented.In Section IV,three tournaments are given to verify the feasibility of adaptive strategy.Section V states the conclusions of our study.

II.ITERATED PRISONER’S DILEMMA

Life is filled with paradoxes and dilemmas.A very lifelike paradox is called “prisoner’s dilemma”,discovered by Melvin Dresher and Merrill Flood[12].The prisoner’s dilemma is a canonical example of two non-zero-sum game.Each agent has two options in each round.One is to cooperate(C),and the other is to defect(D).Based on its choice,the agent will receive a payoff governed by a payoff matrix,as shown in Table I.whereRis the payoff when both agents choose cooperation.When only one of the agents defects,it will receive a payoffT,and the opponent will receive a payoffS.If both of the agents decide to defect,each will receive a payoffP.The basic rule of the payoff matrix isT＞R＞P＞Sand 2R＞T+S.

The standard IPD is played repeatedly between two players,each with its own strategy.They may have different strategies which can be represented by lookup tables,finite-state machines,and neural networks.The IPD based on the strategies which are represented by finite state machines can be analyzed as a Markov process.This allows an average score to be determined for any pair of strategies using standard techniques in stochastic processes[12].Some typical types of the fixed strategies are described in Table II[26].

TABLE I IPD PAYOFF MATRIX

TABLE II SOME FIXED IPD STRATEGIES

Definition 1:Denoted byaas ann-tuple of mixed actions and ifa= (a1,a2,...,an),then the payoff ofacan be written asU=(U1,U2,...,Un).For convenience we introduce the substitution notationa=(a−i;ai),where

Definition 2(Nash Equilibrium)[3]:A joint action set(a−i;ai)is a pure Nash Equilibrium point if,for theith player

During the IPD,a Nash equilibrium(NE)can be achieved by maximizing the payoffs of agents.If the agents are selfish and want to maximize their own payoffs without considering the interests of the others,the mutual defection can be obtained as a NE.Therefore,one of the two following situations will occur:

1)If the opponent chooses C,the agent may have payoffRorT,T＞R,then the agent will choose D.

2)If the opponent chooses D,the agent may have payoffSorP,P＞S,then the agent will choose D.

Therefore,mutual defection leads to the unique NE,which represents a better short-term payoff.However,Axelrod showed that although mutual defection yields a better shortterm reward[3],mutual cooperation is a better solution in the long run.Furthermore,when the IPD presents more than two choices,the evolution of defection may be a result of strategies effectively having more opportunities to exploit others when more choices exist[11].Based on the fixed strategies shown in Table II,each of them has their own personality and can make decisions based on the opponent’s move.However,the fixed strategies are of passive type which means they choose the actions based on history without considering the actions of next step.The main contribution of this paper is designing a competitive adaptive strategy which can predict the actions and achieve mutual cooperation without losing competitiveness.In the next section,the reinforcement learning method is introduced to design the adaptive strategy.

III.TD(λ)METHOD FOR PRISONER’S DILEMMA

During the IPD,the known information includes the decisions and payoffs of the previous steps.Therefore,the goal of our study is solving a multi-step prediction problem regarding how to teach the agent predict its own future scores based on the available options.Learning to predict involves using past experience of the unknown system to predict its future behavior.One advantage of prediction learning is that the training examples can be taken directly from the temporal sequence of ordinary sensory input;no special supervisor or teacher is required.TD learning is a prediction method which combines Monte Carlo and dynamic programming ideas.It learns by sampling the environment according to some policy and then approximates its current estimate based on previously learned estimates.

A.Adaptive Design Strategy by TD(λ)Method

In this paper,the adaptive agent should have some features as follows.An adaptive agent should consider the long-term reward based on the situation.In other words,an adaptive agent should learn cooperative coevolution.For instance,if the agent identifies that the opponent will choose “cooperate”,the adaptive agent should choose cooperate.If the opponent choose “defect”,for protecting its payoff,the adaptive agent should choose “defect”.Learn to cooperate with others is a significance character of human beings.Therefore,for an adaptive agent,learning to cooperate is vital.

As a prediction method,when observation is possible,TD learning can be adjusted to better match the observation.TD methods also are more incremental,easier to compute,and tend to make more efficient use of their experience.

Based on the model mentioned in[1],the TD(λ)learner can be expressed as Fig.1.

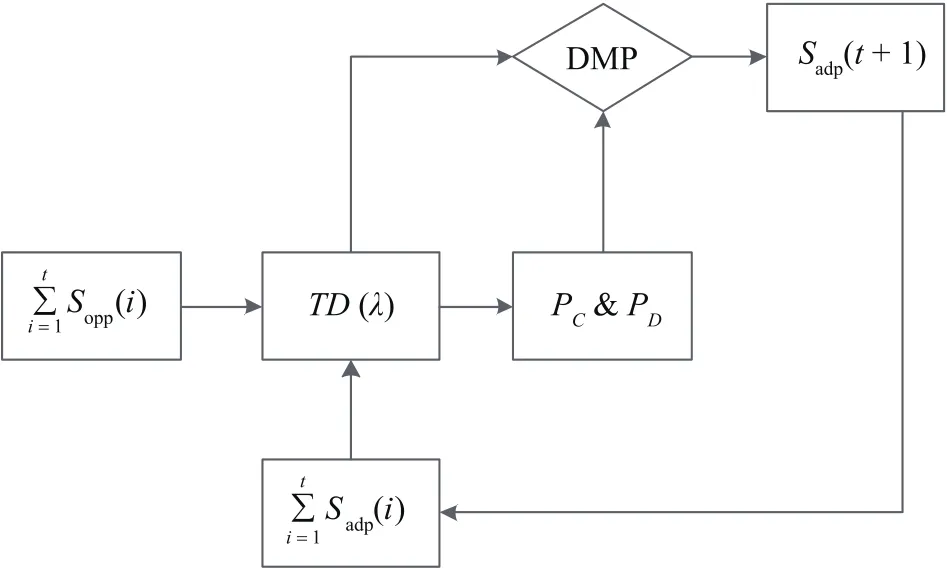
Fig.1.The decision making process for the adaptive agent.

Epochst=1,2,...,T.The scores of the adaptive agents and their opponents areSadp(t)andSopp(t),while the forecasting cooperative and defective earnings of the adaptive agent at timetareScp(t)andSdp(t),respectively.The equation for calculating the forecasting earnings of adaptive agent is shown as follows:

wherePC∈(0,1)andPD∈(0,1)represent the possibility of cooperation and defection,respectively,for the adaptive agent.R,T,SandPare the payoffs of the IPD,as shown in Table I.

Therefore,the TD(λ)learner can be described as follows:

1)Initialization:The state set and action set of theith agent areZ={C,D},whereCis cooperate,andDis defect.The payoff matrix of the agents is shown as Table I.

2)CalculatingScp(t+1)andSdp(t+1)by(2)−(5).

3)The agent makes decision based on the decision making process(DMP).

4)Back to 2)until the iteration stops.

The DMP is shown as follows:

1)IfScp(t+1)＞Sdp(t+1),the adaptive agent will cooperate with the opponent.The possibility of cooperating will increase toPC(t+1)=PC(t)+F(PC(t+1));the possibility of defecting will decrease toPD(t+1)=PD(t)−F(PD(t+1)).

2)IfScp(t+1)＜Sdp(t+1),the adaptive agent will defect with the opponent.The possibility of defecting will increase toPD(t+1)=PD(t)+F(PD(t+1));the possibility of cooperating will decrease toPC(t+1)=PC(t)−F(PC(t+1)).

3)IfScp(t+1)=Sdp(t+1),the adaptive agent will cooperate with the opponent.However,the possibility of defecting cannot be reduced.The possibility of cooperating will increase toPC(t+1)=PC(t)+F(PC(t+1)).Therefore,the adaptive agent can be encouraged to choose cooperation for the long-term team reward.The functionF(ε)is modified Fermi function shown as follows:

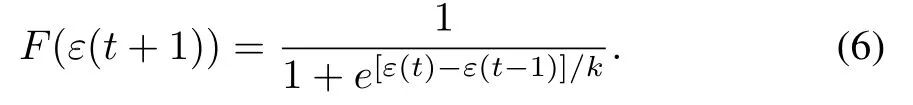
The DMP of adaptive agent clearly indicates that the decisions rely not only on the previous steps,but also on the learning method of the adaptive agent.PDandPCdecide the tendency of the adaptive agent.Moreover,due toandwill decrease.In other words,the effect of the last step is greater than that of the other steps,and effect of the first decision within the IPD becomes increasingly weaker as the number of iterations increases.For investigating the convergence in the mentioned manner,the analytical properties are discussed in following subsection.

B.The Analytical Properties of Adaptive Strategy

Different IPD strategies use different history lengths of memory to determine their choices.In a finite length IPD which hasLrounds,the largest history length which a strategy can access isL.As to the strategy mentioned in this section,the memory size is as long as the length of finite IPD game.A nontrivial question is whether the adaptive strategy can be the counter strategy(CS)against other strategy?It has been proven that every finite history length is possible to occur in an infinite length IPD which can be expressed as following theorem.

Definition 3(Counter Strategy)[26]:A strategySis a counter strategy(CS)against another strategyS1,if for any strategyS′

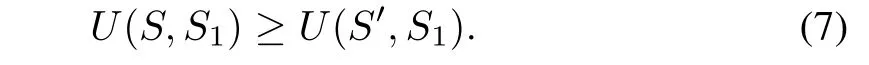
Lemma 1[26]:For any strategy that uses a limited history length,there always exist some strategies with longer memory against which the strategy cannot be a counter strategy.

Theorem 1:The adaptive strategy mentioned in Section II has a higher probability of being a CS against fixed strategy in an infinite length IPD.

Definition 4[26]:Any strategy that uses a limited history cannot be an evolutionarily stable strategy(ESS)in an infinite length or indefinite length IPD.ESS is a strategy such that,if all the members of a population adopt it,then no mutant strategy can invade the population under the influence of natural selection.

Therefore,the condition for a strategySto be ESS is that for anyS′

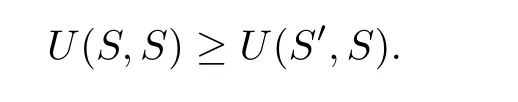
There is a relationship between CS and ESS.A strategy is ESS if it is the only CS against all IPD strategies[26].As to the adaptive strategy,the evolutionary stability is discussed as follows.

Theorem 2:As to IPD consisted of fixed strategies and adaptive strategy,the adaptive strategy mentioned in Section II is ESS.

The adaptive strategy designed in this paper is a kind of strategy with the memory size as the length of the IPD game.During the IPD game,the adaptive strategy has the longest memory compared with other strategies.As to the designed game,the adaptive strategy has a higher possibility to be CS of the other fixed strategies.Therefore,the adaptive strategy will earn a better payoff when played against other fixed strategies.During next section,some simulations are given to illustrate the effectiveness of the mentioned manner.

IV.SIMULATIONS

In order to measure the effectiveness of agents using the adaptive strategy,three IPD tournaments are simulated in different complex networks.The square lattice network and scale-free network are introduced to be the environments of the simulations.Each of the game theoretical tournaments can be represented as tupleG(N,A,F),whereNis the number of the agents,A={C,D}is the action set of the agents,CandDrepresents the cooperate and defect,andFis the payoff function for each action.The practical payoff matrix of the Prisoner’s dilemma is shown in Table III.

TABLE III IPD PAYOFF MATRIX

The simulations based on square lattice network and scale-free networks are given in the following sections.

A.The Simulations Based on the Square Lattice Network

Based on the characteristic of the 100×100 square lattice network,there areN=1,2,...,i,...,10000 agents on the network.In this section,two tournaments are provided to illustrate the effectiveness of the adaptive strategy.During first tournament,the designed adaptive strategy will play against the fixed strategies mentioned in Table II.During the second tournament,two kinds of strategies based on Q-learning[27]and self-adaptive method[28]are given to play against the designed strategy.The structure of the partial square lattice network is described as Fig.2.As to each agent,it has eight neighbors.The coordinates of agents represent the relative position between them.

During each iteration,theith agent plays against its neighbors according to the rules of IPD.Based on the feature of the lattice network,the adaptive agents can play against agents with all kinds of strategies.The cooperative ratepand average fitness value are introduced to illustrate the effectiveness of mentioned manner.

whereptrepresents cooperative rate of thetth iteration;Ncrepresents the number of cooperating agent;Nis the number of all the agents.

wherefave(Stra)means the average fitness value of strategyStra;Stis the payoff oftth round-robin game;Tis the number of total iterations.

Fig.2.The structure of the square lattice network.

1)The Tournaments Between Designed Strategy and Fixed Strategies:In this section,the tournament between designed strategy based on the TD learning method and fixed strategies is provided to verify whether the designed strategy can earn a better payoff than the other fixed strategies.The steps of the tournament are represented as follows:

Step 1:Initializing the number of iteration as 100.Randomly generating the positions of the agents with different strategies.The numbers of agents with different strategies are equal.The initial states of the agents are cooperation and defection.The total initial cooperative rate isp1=0.3.The cooperators will be marked as red squares.The defectors will be marked as blue squares.

Step 2:During each round of the round-robin games,ith agent will play against its neighbors by the prescribed sequence which is shown as Fig.3,and update its states according to the characteristics.

Fig.3.The order of each round-robin game.

Step 3:Calculating the cooperative rates and average fitness values for verifying effectiveness of the mentioned manners.

During the first example,the average fitness values of the different strategies in IPD tournament are given in the Table IV.The statistical results illustrate that adaptive strategy earns a better payoff compared with other strategies.In the tournament,defective actions became extinct after 9 generations,and cooperative actions occupy the majority of the population.

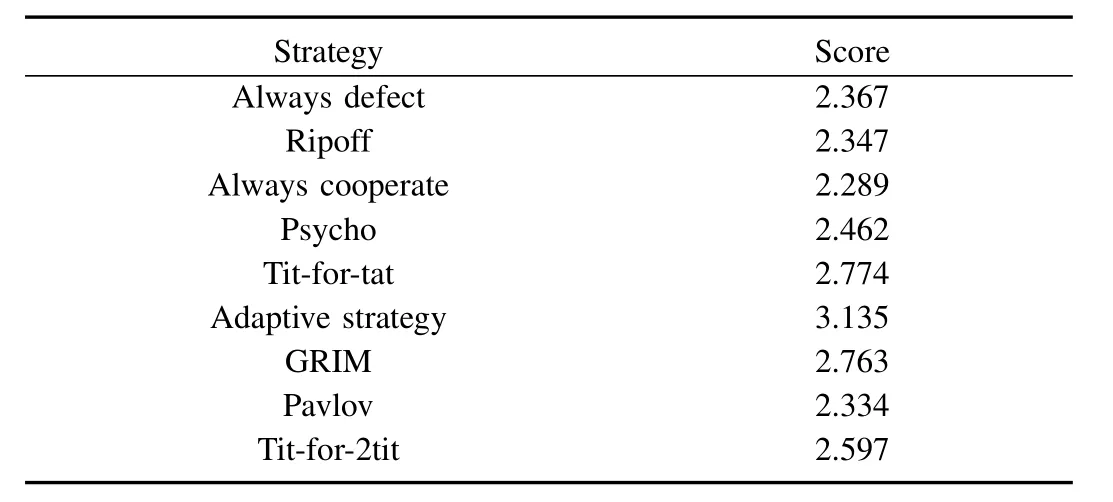
TABLE IV RESULTS OF FIRST ROUND-ROBIN IPD

The simulation results of the first tournament are shown in Fig.4.Therefore,a conclusion can be obtained that mutual cooperation becomes popular among the agents and spreads fast.However,another problem is that how does the initial cooperative ratep1influence the result.Therefore,the simulation results based on the different initial conditions are shown as Fig.5.Fig.5mentions that the three different initial values which arep1=0.3,p1=0.5 andp1=0.8 lead to different balance points.However,the equilibrium points are all above 75 percent which is significantly larger than the percentage of agent with always cooperate.Therefore,mutual cooperation can be achieved between majority of the agents.

2)The Tournaments Between Designed Strategy and Other Evolutionary Learning Methods:In this section,two evolutionary learning methods are introduced into the tournaments.One is a Q-learning strategy[27],and the other one is a self-adaptive w in-stay-shift reference selection strategy[28].The environment of this tournament is also the square lattice network.The steps of the tournament are represented as follows:

Step 1:Initializing the number of iteration as 100.Random ly generating the positions for the agents with different strategies on the square lattice network.Three kinds of evolutionary strategies are evenly distributed on the network.The initial states of the agents are cooperate and defect.The initial cooperative rate isp1=0.3.The cooperators will be marked as green squares.The defectors will be marked as blue squares.

Step 2:During each round of the round-robin,ith agent will play against its neighbors by the prescribed sequence which is shown as Fig.3,and update its states according to their own features.

Step 3:Calculating the cooperative rates and average fitness values of the three different evolutionary strategies.

The simulation results of the second tournament are shown in Fig.6.The simulation results illustrate that the cooperation spreads fast among the agents.The network becomes stable within 5 iterations,and the cooperative rate of 100th iteration is 0.904.The results verify that the mutual cooperation can be achieved between the agents with evolutionary strategies.

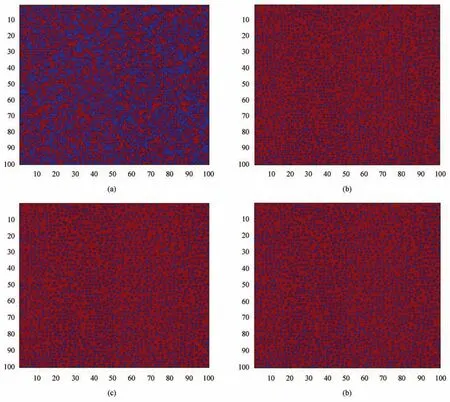
Fig.4.The simulation results of round-robin game.(a)The distributions of the 1st round-robin game.(b)The distributions of the 10th round-robin game.(c)The distributions of the 50th round-robin game.(b)The distributions of the 100th round-robin game.

Fig.5.The cooperative rates based on different initial values.

The average fitness values of the different strategies are shown in Table V.The results show that although the TD Learning Strategy earns a better score,the differences between the scores are minor.The reason of this phenomenon is that the cooperation spreads fast and maintained within 5 rounds.

To sum up,the simulations based on the square lattice network show that the payoff of adaptive strategy is higher than other strategies during the tournament.Most of the agents choose cooperation with others.However,not all the agents choose cooperating with the others.We give another example to verify whether the mutual cooperation can be achieved among the agents with the designed adaptive strategy.

TABLE V RESULTS OF SECOND ROUND-ROBIN IPD

B.The Simulations Based on the Scale-free Networks

For the scale-free networks,the relationships between the agents are not homogenous.The agents prefer to make connections with the agents with advantage of fitness which are named hubs.Therefore,they may have different degrees.This kind of network is widely used in the real world,such as Internet,social networks,and so on.References[29],[30]studied the game behaviors between the two agents on the scale-free network.These studies drew a conclusion that the scale-free network can promote the mutual cooperation by the most successive agents.Reference[29]found that the scale-free networks were extremely vulnerable to attacks,i.e.,to the selection and removal of a few nodes that play the most important role in assuring the network’s connectivity.The conditions of the hubs are significant for the scale-free network.

Fig.6.The simulation results of round-robin game.(a)The distributions of the 1st round-robin game.(b)The distributions of the 5 th round-robin game.(c)The distributions of the 10 th round-robin game.(d)The distributions of the 100 th round-robin game.

The purpose of this experiment is to figure out whether the adaptive agents can achieve mutual cooperation by their own strategies to increase the fault tolerance of the scale-free network.The typical graph of scale-free network is shown as Fig.7[7].

Fig.7.The typical structure of scale-free network.

All the agents in this tournament are adaptive agents.During this tournament,the IPD runs for 100 rounds per trial with different initial values of the cooperative rate.The initial values of cooperative rate are 0.1,0.5 and 0.8,respectively.Based on this situation,the initial states of some hub agents may be defection.Therefore,it is very difficult for the agents to achieve mutual cooperation by the characteristic of the scale-free network.The main propose of this tournament is inspecting whether the mentioned manner can optimize decision making process for helping the agents to obtain mutual cooperation.The steps of the tournament are shown as follows.

Step 1:Initializing the number of iterations as 100.Initializing the states of the agents in the scale-free network.The initial values of the cooperative rates are 0.1,0.5 and 0.8,respectively.

Step 2:During each round of the tournament,ith agent will play against its neighbors,and update its states according to the characteristics.Since all the agents are adaptive agents,the agents will try to achieve mutual cooperation according to optimizing the decision making process.

Step 3:Calculating the cooperative rates for verifying effectiveness of the mentioned manners.

As Fig.8 shows,the cooperative rates will convergence to 1.Therefore,the simulation results of this tournament show that no matter what the initial value is,all the agents will choose cooperation.The experimental results indicate that although the scale-free network encourages the agent to copy the strategies of the hubs which may lead the agents to defect with each other,the adaptive agents can obtain mutual cooperation.They can make their own decisions based on their strategies to increase the fault tolerance of the scale-free network.The experimental results indicate the effectiveness of the adaptive strategies.

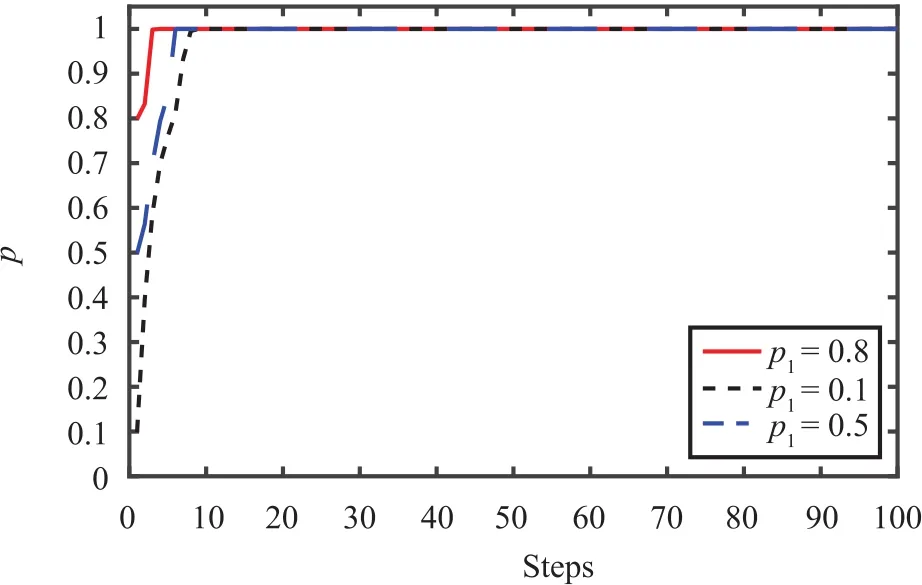
Fig.8.The cooperative rates based on different initial values.

V.CONCLUSION

A reinforcement learning method was introduced to design an adaptive strategy for the IPD.The agent with adaptive strategy can make decisions under a consideration of the longterm reward.In order to verify the effectiveness of this method,three kinds of tournaments under two different environments were discussed in Section IV.The simulation results illustrated that the adaptive agents were able to cooperate with their opponents without losing competitiveness.They could achieve mutual cooperation,which is not only meaningful for the long-term reward of the team,but also the fault tolerance of the scale-free network.In our future research,we will investigate the essential relationship between the IPD and multi-agent systems in different complex networks,as well as the application of game theory for analyzing dynamics of multi-agent system.

APPENDIX A PROOF OF THEOREM 1

As for the infinite length IPD,supposeSLis a fixed strategy with memory-L.The CS againstSLmust play a periodic sequence with period less thanL.Letqi(i=1,...,L),denotes the probability that CS plays a sequence whose period is equivalent toi.

SupposeQL(A|SL)is the probability of adaptive strategy being a CS against a fixed strategySLwith memory-L.As to the strategy with zero memoryS0,there isQL(A|S0)=q/2.IfS0plays a periodic sequence whose period is equivalent to two,theQL(A|S0)=q/4.Furthermore,S0plays a periodic sequence whose period is equivalent toL,QL(A|S0)=qL/2L.

Thus,the highest value ofQL(A|S0)is represented as

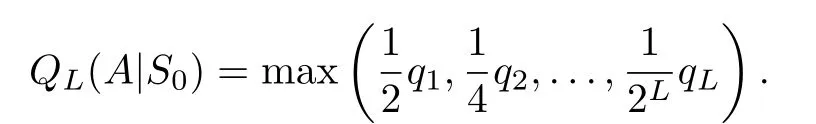
The strategy with memory-1 can shift its play sequence between a determined sequence and a period-two sequence.There fore the maximums ofQL(A|S1)is

There are

For the adaptive strategies,the memory length is as long as the IPD.Therefore,during the infinite length IPD,the adaptive strategy has the lengthKwhich is larger than theL.Therefore,the highest value ofQL(A|SL)isQL(A|SL)=q1/2+q2/4+···+qL/2L

Thus,

Due to

based on the former information

There must beQ(A)=Q(SK)＞Q(SL)for any limited numberLin an infinite length IPD.Therefore,the adaptive strategies have a higher probability of being a CS against fixed strategy in certain conditions.The concepts of CS can be used to verify the evolutionary stability of the adaptive strategy.

APPENDIX B PROOF OF THEOREM 2

Based on the Theorem 1,for any fixed strategyS′,

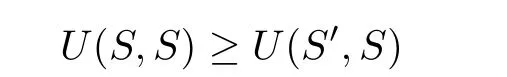
and

According to[26],the condition for a strategySto be ESS is that for anyS′

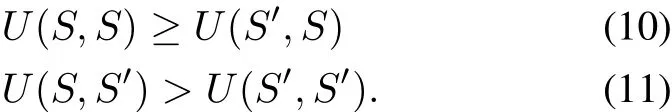
Comparing with the inequalities with(10)and(11),the adaptive strategy is ESS,when played against other fixed strategy.Therefore,the adaptive strategy is ESS under certain condition.

[1]J.Seiffertt,S.Mulder,R.Dua,and D.C.Wunsch,“Neural networks and Markov models for the iterated prisoner’s dilemma,”inProc.Int.Joint Conf.Neural Networks,Atlanta,GA,USA,2009,pp.2860−2866.

[2]H.Y.Quek,K.C.Tan,C.K.Goh,and H.A.Abbass,“Evolution and incremental learning in the iterated prisoner’s dilemma,”IEEE Trans.Evol.Comput.,vol.13,no.2,pp.303−320,Apr.2009.

[3]R.Axelrod,The Evolution of Cooperation.New York,USA:Basic,1984.

[4]M.A.Nowak,R.M.May, “Evolutionary games and spatial chaos,”Nature,vol.359,no.6398,pp.826−829,Oct.1992.

[5]F.Fu,M.A.Nowak,and C.Hauert,“Invasion and expansion of cooperators in lattice populations:Prisoner’s dilemma vs.snowdrift games,”J.Theor.Biol.,vol.266,no.3,pp.358−366,Oct.2010.

[6]J.Liu,Y.Li,C.Xu,and P.M.Hui,“Evolutionary behavior of generalized zero-determinant strategies in iterated prisoner’s dilemma,”Phys.A Stat.Mech.Appl.,vol.430,pp.81−92,Jul.2015.

[7]G.Szabó,G.Fath,“Evolutionary games on graphs,”Phys.Rep.,vol.446,no.4−6,pp.97−216,Jul.2007.

[8]D.C.Wunsch and S.Mulder,“Evolutionary algorithms,Markov decision processes,adaptive critic designs,and clustering:Commonalities,hybridization and performance,”inProc.Int.Conf.Intelligent Sensing and Information Processing,Chennai,India,2004,pp.477−482.

[9]H.Ishibuchi and N.Nam ikawa, “Evolution of iterated prisoner′s dilemma game strategies in structured demes under random pairing in game playing,”IEEE Trans.Evol.Comput.,vol.9,no.6,pp.552−561,Dec.2005.

[10]H.Ishibuchi,H.Ohyanagi,and Y.Nojima,“Evolution of strategies with different representation schemes in a spatial iterated prisoner’s dilemma game,”IEEE Trans.Comput.Intell.AIGames,vol.3,no.1,pp.67−82,Mar.2011.

[11]D.Ashlock and E.Y.Kim,“Fingerprinting:Visualization and Automatic analysis of prisoner’s dilemma strategies,”IEEE Trans.Evol.Comput.,vol.12,no.5,pp.647−659,Oct.2008.

[12]D.Ashlock,E.Y.Kim,and W.Ashlock,“Fingerprint analysis of the noisy prisoner’s dilemma using a finite-state representation,”IEEE Trans.Comput.Intell.AI Games,vol.1,no.2,pp.154−167,Jun.2009.

[13]D.Ashlock and C.Lee,“Agent-case embeddings for the analysis of evolved systems,”IEEE Trans.Evol.Comput.,vol.17,no.2,pp.227−240,Apr.2013.

[14]J.S.Wu,Y.Q.Hou,L.C.Jiao,and H.J.Li,“Community structure inhibits cooperation in the spatial prisoner’s dilemma,”Phys.A Stat.Mech.Appl.,vol.412,pp.169−179,Oct.2014.

[15]Y.Z.Cui and X.Y.Wang,“Uncovering overlapping community structures by the key bi-community and intimate degree in bipartite networks,”Phys.A Stat.Mech.Appl.,vol.407,pp.7−14,Aug.2014.

[16]S.P.Nageshrao,G.A.D.Lopes,D.Jeltsema,and R.Babuška,“Porthamiltonian systems in adaptive and learning control:A survey,”IEEE Trans.Autom.Control,vol.61,no.5,pp.1223−1238,May2016.

[17]C.M.Liu,X.Xu,and D.W.Hu,“Multi objective reinforcement learning:A comprehensive overview,”IEEE Trans.Syst.Man Cybern.Syst.,vol.45,no.3,pp.385−398,Mar.2015.

[18]Y.J.Liu,Y.Gao,S.C.Tong,and Y.M.Li,“Fuzzy approximation-based adaptive back stepping optimal control for a class of nonlinear discrete time systems with dead-zone,”IEEE Trans.Fuzzy Syst.,vol.24,no.1,pp.16−28,Feb.2016.

[19]Y.Gao and Y.J.Liu,“Adaptive fuzzy optimal control using direct heuristic dynamic programming for chaotic discrete-time system,”J.Vibrat.Control,vol.22,no.2,pp.595−603,2016.

[20]Y.J.Liu,L.Tang,S.C.Tong,C.L.P.Chen,and D.J.Li,“Reinforcement learning design-based adaptive tracking control with less learning parameters for nonlinear discrete-time M IMO systems,”IEEE Trans.Neural Netw.Learn.Syst.,vol.26,no.1,pp.165−176,Jan.2015.

[21]K.G.Vamvoudakis,F.L.Lew is,and G.R.Hudas,“Multi-agent differential graphical games:Online adaptive learning solution for synchronization with optimality,”Automatica,vol.48,no.8,pp.1598−1611,Aug.2012.

[22]P.Hingston and G.Kendall,“Learning versus evolution in iterated prisoner’s dilemma,”inProc.Congr.Evolutionary Computation,Portland,OR,USA,2004,pp.364−372.

[23]S.Y.Chong and X.Yao,“Multiple choices and reputation in multiagent interactions,”IEEE Trans.Evol.Comput.,vol.11,no.6,pp.689−711,Dec.2007.

[24]E.Semsar-Kazerooni and K.Khorasani,“Multi-agent team cooperation:A game theory approach,”Automatica,vol.45,no.10,pp.2205−2213,Oct.2009.

[25]D.Ashlock,J.A.Brown,and P.Hingston,“Multiple opponent optimization of prisoner’s dilemma playing agents,”IEEE Trans.Comput.Intell.AIGames,vol.7,no.1,pp.53−65,Mar.2015.

[26]J.W.Liand G.Kendall,“The effect of memory size on the evolutionary stability of strategies in iterated prisoner’s dilemma,”IEEE Trans.Evol.Comput.,vol.18,no.6,pp.819−826,Dec.2014.

[27]K.Moriyama, “Learning-rate adjusting Q-learning for prisoner’s dilemma games,”inProc.IEEE/WIC/ACM Int.Conf.Web Intelligence and Intelligent Agent Technology,Sydney,NSW,Australia,2008,pp.322−325.

[28]X.Y.Deng,Z.P.Zhang,Y.Deng,Q.Liu,and S.H.Chang,“Self-adaptive w in-stay-lose-shift reference selection mechanism promotes cooperation on a square lattice,”Appl.Math.Comput.,vol.284,pp.322−331,Jul.2016.

[29]F.C.Santos and J.M.Pacheco,“Scale-free networks provide a unifying framework for the emergence of cooperation,”Phys.Rev.Lett.,vol.95,no.9,pp.Article ID 098104,Aug.2005.

[30]F.C.Santos and J.M.Pacheco,“A new route to the evolution of cooperation,”J.Evol.Biol.,vol.19,no.3,pp.726−733,May2006.