现代有轨电车合理站间距研究

2018-01-26甘元佳易思蓉

铁道标准设计 2018年2期

甘元佳,易思蓉

(1.西南交通大学土木工程学院,成都 610031； 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

1 概述

截至2016年底，我国开通运营现代有轨电车线路的城市增加至11个，计有17条线，共235.6 km，268座车站[1](表1)；整体而言，我国现代有轨电车事业蓬勃发展，方兴未艾。研究现代有轨电车的车站分布对提高其投资效益、促进城市的可持续发展有重要意义。

现代有轨电车是在传统有轨电车的基础上，通过全面的技术改造、升级而发展起来的一种中低运量轨道交通系统。相比传统有轨电车，它具有以下特点[2]。

(1)采用模块化低地板车辆，设计更加人性化。

(2)可以采用独立或者半独立路权，辅以交叉口信号优先，提高了运行速度和服务水平。

(3)采用流线型设计和绿化道床，且供电方式多样，满足城市景观需求。

(4)载客能力可通过增减车辆模块和车辆联挂运行进行调节。

表1 2016年中国现代有轨电车运营线路统计

2 车站分布相关因素分析[5]

2.1 现代有轨电车车站概述

受运营组织的影响，现代有轨电车的车站形式比较简单，除首末站和部分重要的换乘车站设置少量设备及管理用房外，中间站仅设置站亭、照明、导向、无障碍设施和辅助安全设施等满足乘客上下车及候车要求。

2.2 对吸引客流的影响

现代有轨电车通过车站吸引大量客流，对缓解城市交通压力发挥着重要作用，所以在大型客流集散点必须设站；其他车站的设置主要受人们对站间距的要求支配，需要兼顾各车站间距离的均匀性。

车站客流吸引范围模型简单假定为以车站为圆心，乘客平均到站距离为半径的圆形覆盖面积(图1)。普通人的正常步行速度一般是4～7 km/h，并考虑城市道路非直线系数的折减。《城市道路交通规划设计规范》(GB50220—95)规定：公共交通线路非直线系数不应大于1.4，整个线网的平均非直线系数以1.15～1.20为宜。由此计算出车站对步行客流的吸引范围，与车站周边半径750 m以内的10 min步行圈[7]的提法一致。

图1 车站对步行客流的吸引范围示意

相邻车站客流吸引范围重叠部分面积的一半为

(1)

单个中间站对步行客流的吸引范围为

S2=πr2-2S1

(2)

整条线路对步行客流的吸引范围为

(3)

全线预测客流量与客流吸引范围面积成正比，若全线预测客流量Q0所依据的基础车站分布的平均站间距为d0，按公式(3)计算得到对应的客流吸引范围面积S0，则站间距对客流量的影响可以表示为

(4)

对于地铁的平均站间距离，国际上有两种趋向：一种是小站间距，平均为1 km左右；一种是大站间距，平均为1.6 km左右。但对于现代有轨电车的大小站间距到底取值多少，暂时没有明确的概念。而由表1可知，我国开通运营的现代有轨电车线路的平均站间距除大连(改造线)和苏州高新区(远期设站22座)外，大多数在0.5～0.9 km。为明确概念，本文所言现代有轨电车的小站间距指0.5 km左右，大站间距则为0.9 km左右。

2.3 对乘客出行时间的影响

乘客单程出行时间可以分为接驳时间、候车时间和乘车时间3部分。

2.3.1 对接驳时间的影响

增加车站的设置密度，减小站间距，可以缩短接驳距离；而最主要的接驳方式是步行和自行车，接驳速度一般固定，因此小站间距无疑会节省接驳时间。

2.3.2 对候车时间的影响

候车时间主要与乘客到站时刻和发车时刻之差有关。

我国有轨电车大部分处于运营初期，早晚高峰时段的运营间隔一般在7～15 min；但随着线路成网，客流逐步增长，发车间隔也会逐渐缩短。

法国现代有轨电车的重建比我国要早30年，在应用和形式上比我国成熟多样。表2统计了2015年春季法国部分城市现代有轨电车的运营状况[8]，可以佐证我国有轨电车线路成网、客流成熟后的运营情况。

由此认为当客流需求成熟后，现代有轨电车在正常工作日的实际运行间隔一般为3～10 min。乘客到站时刻可以认为是随机的；对乘客总体来说，乘客的到站时刻可以认为在发车间隔内均匀分布，那么平均候车时间就等于发车间隔的一半(2～5 min)。

2.3.3 对乘车时间的影响

当采用大站间距时，一方面可以充分发挥列车的性能以提高走行速度，另一方面设站较少还能减少因制动减速和起动加速以及在各车站停车所产生的延迟，从而缩短乘车时间。

表2 法国部分城市有轨电车运营状况

注：运营间隔时间按周一至周五/周六/周日依次表示。

下面通过一个案例来定量分析不同站间距对列车速度和乘车时间的影响。

假定基础资料：线路全长18 km，平均站间距分别取0.4，0.5,…，1.0 km，根据中车株洲电力机车研究所对有轨电车牵引系统的研究[9]，列车牵引特性曲线如图2所示，列车运行的最高速度取为70 km/h，常用制动平均减速度(70～0 km/h，包括响应时间)采用1.2 m/s2(假定适用于所有负载情况)，为了简化计算，假定线路条件为平直空旷地段。

图2 列车牵引/电制动特性曲线

牵引计算方法如下[10]。

列车单位基本阻力

R=2.7+0.000 42V2(N/kN)

(5)

式中V——列车速度，km/h。

根据列车运动方程式，区段运行时间Δt和区段运行距离Δs的计算公式为

(6)

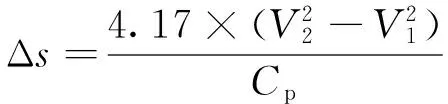
(7)

式中 Δt——区段运行时间，min;

V1——速度间隔内的起点速度，km/h；

V2——速度间隔内的终点速度，km/h；

Cp——速度间隔内的平均速度所对应的单位合力，Cp=F-R(N/kN)；

Δs——区段运行距离,m。

当牵引计算的速度间隔为ΔV=1.0 km/h时，计算结果如表3所示。计算表明，有轨电车能实现70 km/h速度的最小站间距为0.631 km。

表3 不同站间距对有轨电车运行速度的影响

牵引计算中并未考虑有轨电车在道路交叉口的延误，可以视作采用独立路权时所能达到的理论值。采用半独立路权或混行路权时，路口延误与线路经过的交叉口数量和在交叉口采取的信号优先等级有关。

从表3和图3可以看出，有轨电车单向全程走行时分随平均站间距的增加而减小，但减小的幅度逐渐降低，这说明增大站间距不能无限制地减少乘车时间。若乘客的平均乘距为9 km，则采用d=0.5 km将比采用d=0.9 km增加乘客出行时间7.0 min(d为平均站间距)。

图3 不同站间距单向走行时分曲线

车辆过交叉口速度根据《城市道路工程设计规范》(CJJ37—2012)规定，交叉口内的计算行车速度应按各级道路计算行车速度的0.5～0.7倍计算，直行车取大值，转弯车取小值。考虑到现代有轨电车的制动距离大于普通社会车辆，为保证运营的安全性，在交叉口的限速取30 km/h。有轨电车遇到的信控路口数量与线路经行区域有关，在信控路口的延误时间与信号优先措施有关。成都IT大道有轨电车项目沿线交叉口统计见表4。

表4 IT大道有轨电车项目沿线交叉口统计

经过分析，采用公交信号优先后，成都IT大道现代有轨电车沿线的交叉口信号延误可以降低约20%，根据对沿线交叉口的分析，交叉口的平均延误取20 s。若按每公里1.5个信控路口计，则全线18 km的路口延误估算为18×1.5×20 s=540 s，旅行速度计算结果见表5。

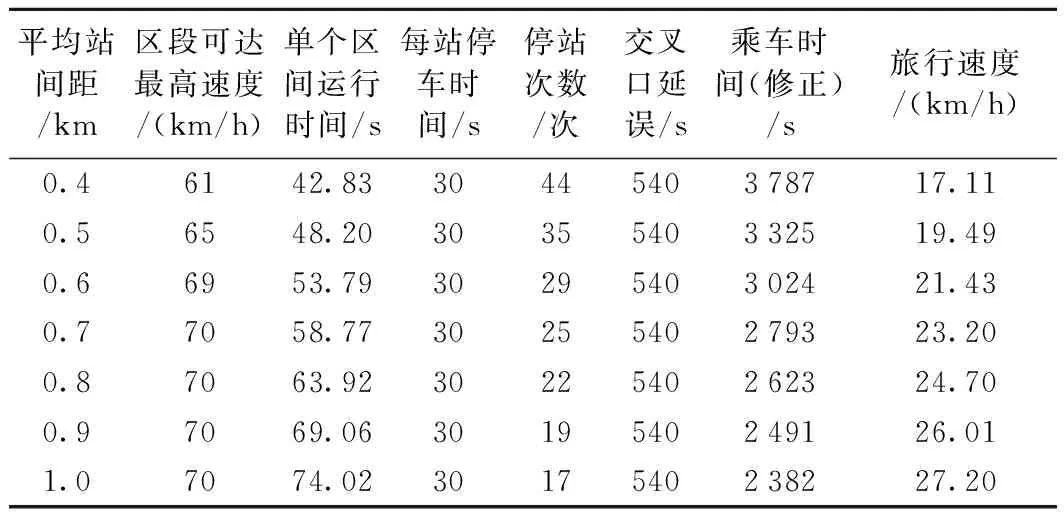
表5 考虑路口延误后的旅行速度

实际运营时，由于在右进右出的非信控路口也有限速的要求以及坡度、曲线的影响，旅行速度会更小一些。

综上所述，现代有轨电车乘客出行总时间为[11]

(8)

式中T——乘客单程出行总时间，s；

l0——乘客平均到站行程，m；

v0——乘客平均到站速度，m/s；

t0——发车间隔，s；

l——乘客平均在线行程，m；

d——平均站间距，m；

S——停站时间，s；

B——启动及制动总时间，s；

A——启动及制动过程中所行距离，m；

V——车辆运行的稳定速度，m/s；

n——造成延误的路口数量，个；

t1——每个路口的平均延误时间，s。

对于现代有轨电车系统，其最大运行速度、加速度一定，S、B、A、V可以确定；对某个具体城市，乘客平均出行距离l相对稳定，人的步行速度也相对固定；l0与车站的吸引范围有关，通常取d/4；线路走向确定后，沿线会造成延误的信控路口数量n也能统计出来。由此，上式可简化为只有平均站间距d一个变量的函数。

(9)

其中，B和A都是反映列车牵引和制动的性能，虽然加速时是按牵引计算的方法进行，与常用减速度代入定值不同；但此时为了分析各参数对最优站间距的影响，按加减速度相同处理，均为a，则由运动学公式可知B=2V/a，A/V=V/a，代入公式(9)可得

(10)

(11)

公式(11)表明最优站间距d只与平均到站速度v0、列车匀速运行速度V、乘客平均在线行程l、停站时间S以及有轨电车的牵引制动性能(加减速度)a这5个参数有关。

由表6可知，最优站间距d随平均到站速度v0、列车匀速运行速度V、乘客平均在线行程l和停站时间S的增加而单调递增，随有轨电车的牵引制动性能(加减速度)a增强而单调递减。上述结论为现代有轨电车确定合理的站间距提供了理论支持，可以据此提出新的方法和建议。

表6 各参数变化对d的影响

例如，(1)根据d-v0的关系，结合时下兴起的共享单车，采用具有中国特色的P+R(Park & Ride)模式，即“停(自行)车换乘(轨道交通)”模式，来取代传统步行集散方式可以提高平均到站速度，从而增大最优站间距，同时也增加了轨道交通站点的吸引范围；(2)根据d-V的关系，在有条件的平交道口采取信号优先措施，可以提高有轨电车的旅行速度，从而增大最优站间距；(3)根据d-l的关系，对于跨组团出行，现代有轨电车是以长距离乘客为主要服务对象，车站分布宜稀疏一些，以提高乘客的旅行速度，而在组团内部的线路车站分布宜密集一些；(4)根据d-a的关系，提高列车的牵引制动性能，可以更好地适应大坡道和平交道口的安全停车要求，减小最优站间距。

2.4 对工程造价的影响

由于车站形式比较简单，在成都市IT大道有轨电车项目[12]的概算中，车站工程仅占总体工程费用的2.0%；所以此节所论工程造价只限于车站本身造价，考虑对车站规模和数量的影响。

采用大站间距可以减少车站数量，从而节约车站的土建工程投资；但同时也将引起部分客流向邻近车站转移，使相邻车站的交通负荷增大，车站规模可能需要相应扩大。

车站有效站台长度不小于远期列车编组长度。现代有轨电车基本长度32～44 m，车辆模块数5模块～7模块。采用1辆编组有轨电车运营的线路，站台长度通常为38 m；采用2辆编组有轨电车运营的线路，站台长度通常为70 m。站台宽度应以车站远期最大设计客流量为依据计算，满足上、下车乘客的需要。

实际有轨电车工程中站台计算宽度通常不构成限制，绝大多数站台都是按地方规范要求将站台宽度取为定值，设计为标准站台，除非遇到客流量特别大的情况。因此站间距对车站工程费用的影响主要体现在车站数目的增减上。

最常用的地面车站的工程费用，包括地面车站土建工程、动力照明和是否安装安全栏杆或半高安全门等辅助设备3部分，通过相应的工程量和概算指标计算得到。

(12)

式中α1——地面车站土建工程费用，元/m2；

α2——动力照明安装费用，元/m2；

α3——安全栏杆购置安装费用，元/座；

α4——半高安全门购置安装费用，元/座；

L——正线长度，km。

2.5 对项目运营的影响

2.5.1 对车辆配置数的影响

大站间距会提高列车的旅行速度，从而减少列车周转时间，故在发车间隔不变的情况下，相应的车辆配置数就会减少，降低运营成本。而站间距离缩短会因频繁起停车而增加电能消耗和轮轨磨耗等，还有车上司乘人员的人工费，都会增加运营成本；但这部分费用相比车辆购置费而言很少，概算时暂且忽略不计。

车辆按运用上的区别，分为运用车、检修车和备用车三类。运用车是指为完成日常运输任务所必须配备的技术状态良好的可用车辆。其计算方法如下[13]。

营业时间内各小时应开行列车对数为

ni=Q1max/(pβ)

(13)

式中Q1max——单向最大断面客流量，人；

P——列车定员数(=列车编组辆数×车辆定员数)；

β——线路断面满载率(通常不宜大于1.4)。

运用车辆数为

(14)

式中n高峰——高峰小时开行列车对数，对；

m——列车平均编组辆数，辆；

θ1——列车周转时间，s。

结合公式(13)和公式(14)，可得

(15)

《成都现代有轨电车工程设计规范》中的定员标准：5模块车辆定员300人，7模块车辆415人。

列车周转时间θ1是指列车在线路上往返一次所消耗的全部时间。

θ1=∑t区间+∑t中间站+∑t折返站

(16)

根据董皓[14]对某城市有轨电车线路的折返能力进行的实地测试，结果见表7。该线基本采用平交路口信号优先模式，运营车辆主要为低地板车辆，全长28.8 m，车体分为3节，双侧共有6个门，乘客可以从前后2个门上车，从中间2个门下车，测试对象X站和T站分别为该线路末端的2个折返站，其中X站为岛式站台，站后设置单渡线，即采用单一渡线站后折返形式。该站站前约60 m即有十字交叉口，因此电车进出该站时可能受到交叉口流量和信号的影响;T站为侧式站台，站前设置单渡线，即采用单一渡线站前折返形式，前后方100 m内无交叉口，但紧靠一个大型交通枢纽，乘客多数携带行李，因此上下客时间可能会受到影响。

表7 现代有轨电车折返流程时间测设结果

X站总耗时max(40，15)+105+max(180，30，10)+115+68=508 s

T站总耗时320+max(47+65，129，30)+314=763 s

因此现代有轨电车折返作业时间，可参考取值为500～800 s。

检修车和备用车的数量一般控制在运用车的10%左右，则所需现代有轨电车总辆数

N=1.2N1

(17)

2.5.2 对票价的影响

车站分布对运营效益的影响主要体现在对车费收入的影响上。车费收入由客流量和票价决定，在(2.2)节中已经讨论过站间距对客流量的影响，这里继续研究其对票价制式的影响。

城市轨道交通票价制式主要采用单一票价制或计程票价制两种。

乘客的平均在线行程为l，平均车站间距d，则可以建立票价和乘距、站间距的函数关系式

p=φ(l，d)

(18)

上海轨道交通实行按里程计价的多级票价，0～6 km 3元，6 km之后每10 km增加1元。票价的计算采用最短路径法，即：当两个站点之间有超过1条换乘路径时，选取里程最短的一条路径作为两站间票价计算依据。上海轨道交通票价结构见表8。

表8 上海轨道交通票价结构

(19)

广州地铁1号线曾在2006年12月30日以前实行按区间分段计价：即起价2元，每进入下一段加收1元，每相邻两站之间为1个区间，每3个区间为1段，全线总票价为6元。广州地铁1号线标票价结构见表9。

表9 广州地铁1号线票价结构

(20)

由于有轨电车的旅行速度相对常规公交提高不是特别明显，当有轨电车票价明显高于常规公交票价时，有轨电车客流会有较大幅度减低，会有相当部分客流转移到常规公交，为此建议有轨电车票价采用与常规公交基本一致的票价体系。在城市修建有轨电车的初期，由于线路未能成网，只有单独的1条或2条线路，为了保持竞争力多采用单一票价制，并给予换乘优惠。

3 现代有轨电车站间距优化模型

3.1 车站分布的费用效益分析

不同利益群体(乘客、运营商和政府)对现代有轨电车车站分布的要求不同[15]：

(1)乘客更看重交通效益。从满足城市日益增长的交通需求，缩短乘客旅途时间，提高城市交通运输效益的角度来看，车站分布应使乘客出行时间最少，实现运输工作量最大化。这就要求现代有轨电车系统能够提供快速、便捷的服务以及吸引乘客的其他因素。

(2)从运营商的角度看，车站分布应使运营的经济效益最大化。在现代有轨电车系统达到所期望的运营水平下，使总体消耗的系统费用最少。

(3)政府则希望能够创造更多的社会效益、环境效益等积极影响。从短期来看，如缓解快速路的拥堵；从长远来看，如实现人口高流动率、土地合理利用、可持续发展、高生活质量等。

基于费用效益的可量化和与站间距的直接相关度，本文选定车站工程费用、运营费用(车辆购置费)，运营收入(车费收入)和乘客节约出行时间效益4部分进行定量分析。

3.2 模型的建立

本文以运营效率最优兼顾乘客节约出行时间效益为目标，从车站工程费用、运营费用(车辆购置费)，运营收入(车费收入)和乘客节约出行时间效益4个部分建立计算模型。

(1)车站工程费用

根据2.4节的分析可得

(2)车辆购置费

2.5.1节中分析了车站分布对车辆配置数的影响，在此基础上，计入现代有轨电车采购单价c1(万元/辆)，则车辆购置费为

tram=1.2×N1×c1

(21)

(3)车费收入

2.2节中分析了客流量与站间距的关系，2.5.2节中车站分布对票价的影响；如此，远期计算年度的车费收入可表示为

ticket=Q×p×365

(22)

(4)乘客节约出行时间效益

2.3节推导了现代有轨电车乘客出行总时间公式

若乘客采用常规公交车出行，常规公交车的旅行速度为Vg(km/h)，步行到达(离开)公交站的时间取tg(min)，发车间隔取ΔTg(min)，则采用公交车出行的总时间为

(23)

乘客的时间价值θ2与所在地区的经济发展程度有关，可按线路经行地区的人均GDP概略估算。

(24)

例如，2016年成都人均国民生产总值(GDP)为77 470元，参考2016年新劳动法中对于工作时间的规定，《国务院关于职工工作时间的规定》第3条修改为：“职工每日工作8 h、每周工作40 h”，则成都地区乘客的时间价值可以估算为

则远期计算年度乘客节约出行时间效益可表示为

(25)

综上所述，有轨电车站间距优化模型的目标函数为

maxF(d)=time+ticket-staiton-tram

s.t. 0.4≤d≤1.0

(26)

式中,各项的含义和计算模型与前文相同。

3.3 模型的求解和分析

为了对模型进行实证分析，本节参考成都市IT大道有轨电车工程的实际情况确定模型中的参数取值，并利用Matlab编程求解。

3.3.1 基础资料

成都市IT大道现代有轨电车工程呈Y型布局，起于西客站，终于郫县西站和红光站，线路全长约39.0 km，共设站46座(其中地面站45座，高架站1座)，车站逐期加密，开通年39座，近远期46座(其中1座高架近远期预留站，其余均为地面站)。开通年(2018年)全日客流量8.64万人次/d，近期(2023年)17.52万人次/d，远期(2038年)26.40万人次/d。按远期计算，平均运距l=5 162 m/人次。

根据前文的分析，参考成都市IT大道现代有轨电车工程的相关资料，确定各参数取值，来验证模型的适用性。

计算的基础资料：线路采用专用路权，全线地面敷设，车站均为地面站，采用标准侧式站台，线路长度L=39.0 km，实际平均站间距d0=0.85 km，远期客流量Q0=26.40万人次/d，高峰小时单向最大断面客流3 457人次，乘客平均在线行程(运距)l=5 162 m；运营按长交路站站停方案组织，于首末站折返，平均发车间隔取5 min，折返作业时间取700 s；车站客流吸引范围为半径r=750 m，每千米1.5个信控路口，每个信控路口平均延误20 s，地区人均GDP为77 470元。

(1)车站均采用标准侧式站台，远期长38 m，宽3.5 m，造价指标178.5万元/座。

(2)乘客节约出行时间效益

若乘客采用常规公交车出行，常规公交车的旅行速度为Vg=15 km/h，步行到达(离开)公交站的时间取tg=5 min，发车间隔取ΔTg=10 min，则采用公交车出行的总时间为

(3)车辆购置费

现代有轨电车采购单价c1按2 000万元/辆计算。

tram=1.2×N1×2 000

(4)票价收入

全程采用单一票价制，票价p=2元/人。则远期计算年度的票价收入为

ticket=Q×2×365

3.3.2 计算结果(表10)

表10 现代有轨电车车站分布费用效益计算

从表10可以看出：(1)从乘客的角度，以要求出行时间最少为目标，则平均站间距取0.5 km为宜；(2)从车站分布的总效益最大来考虑，则平均站间距取0.8 km为宜。乘客出行时间与平均站间距关系曲线见图4。

图4 乘客出行时间与平均站间距关系曲线

加大计算精度，得到：平均站间距取better_d1=0.53 km时，乘客出行时间最小Tmin=16.71 min；车站平均站间距与总效益关系曲线见图5。

图5 车站分布总效益曲线

平均站间距取better_d2=0.84 km，车站分布的总效益最大Fmax=50 581万元。

模型计算结果better_d2=0.84 km与IT大道有轨电车工程的实际平均站间距0.85 km高度吻合；说明当项目具体情况确定后，通过该模型能计算出一个合理的平均站间距取值，用于车站分布的优化。

4 结论

(1)牵引计算表明，有轨电车能实现70 km/h速度的最小站间距为0.631 km。一般现代有轨电车的合理站间距为0.5～0.9 km。

(2)乘客出行时间最短的最优站间距d随平均到站速度v0、列车匀速运行速度V、乘客平均在线行程l和停站时间S的增加而单调递增，随有轨电车的牵引制动性能(加减速度)a增强而单调递减。上述结论为现代有轨电车确定合理的站间距提供了理论支持，可以据此提出新的方法和建议。

(3)以运营效率最优兼顾乘客节约出行时间效益为目标，从车站工程费用、运营费用(车辆购置费)，运营收入(车费收入)和乘客节约出行时间效益4个部分建立了站间距优化模型；并用Matlab编程求解，结合成都市IT大道现代有轨电车工程的相关资料，对模型进行实证分析。结果表明：该优化模型计算结果与工程实际吻合度较高，可以为现代有轨电车车站分布提供借鉴和参考。

[1] 庞瑾，顾保南.2016年中国城市轨道交通运营线路统计和分析—中国城市轨道交通“年报快递”之四[J].城市轨道交通研究，2017(1)：1-5.

[2] 王风云.现代有轨电车主要线路技术条件[J].都市快轨交通，2015，28(1)：72-76.

[3] 王灏，田振清，周楠森，等.现代有轨电车系统研究与实践[M].北京：中国建筑工业出版社，2011.

[4] 陆云.现代有轨电车工程[M].成都：西南交通大学出版社，2015.

[5] 潘琢.城市轨道交通站点分布优化研究[D].成都：西南交通大学，2013.

[6] 何山.城市轨道交通车站多目标布局研究[D].成都：西南交通大学，2015.

[7] 日建设计站城一体开发研究会.Integrated Station-City Develo-pment， The Next Advances Of TOD站城一体开发——新一代公共交通指向型城市建设[M].北京：中国建筑工业出版社，2014.

[8] [法]克里斯多夫·格罗内克，[德]罗伯特·施瓦德.法国有轨电车图集[M].北京：中国铁道出版社，2016.

[9] 袁文烨，陈文光，夏文杰，等.集成式双向DC_DC储能低地板有轨电车牵引系统[J].机车电传动，2016(4)：73-76.

[10] 易思蓉.铁路选线设计[M].3版.成都：西南交通大学出版社，2009.

[11] 易思蓉.城市轨道交通线路规划与设计[M].北京：科学出版社，2013.

[12] 成都市市政工程设计研究院.成都市IT大道现代有轨电车项目工程可行性研究报告[R].成都：成都市市政工程设计研究院，2015.